网易公开课视频地址:http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址:http://cs229.stanford.edu/ 课程讲义下载地址:https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/image/Stanford/cs229-notes1.pdf
Lecture 2 -Supervised Learning Setup. Linear Regression.
监督学习
当给定一组数据集,包括47个房屋的大小和价格,如何利用监督学习来根据大小估计价格呢?
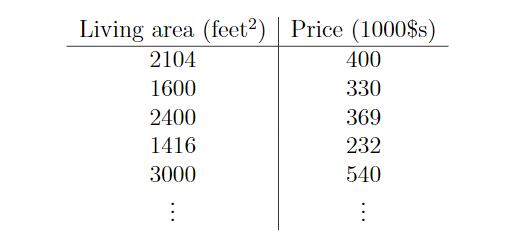 首先我们可以将这些数据映射到二维空间中,x轴代表size,y轴代表price。
首先我们可以将这些数据映射到二维空间中,x轴代表size,y轴代表price。
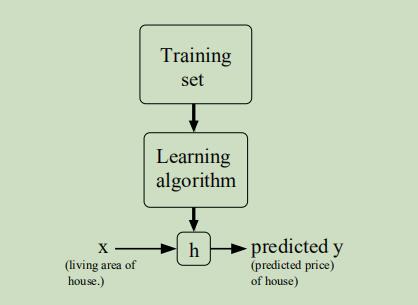
 然后将这些训练样本通过学习算法生成假设函数,对假设函数输入变量x,并得到预测的结果y。
然后将这些训练样本通过学习算法生成假设函数,对假设函数输入变量x,并得到预测的结果y。
当目标变量是连续时,称此类学习问题为回归问题(regression problem) 当y只能是少量的离散变量时(给定居住大小,输出是公寓还是别墅),称此类为分类问题(classification problem)
线性回归(Linear Regression)
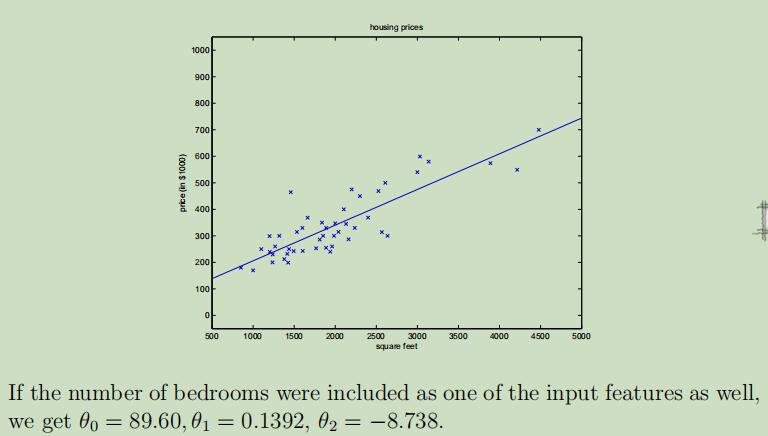
假设现在估计房屋价格需要使用两个变量:面积 and 卧室数量,数据集如下:
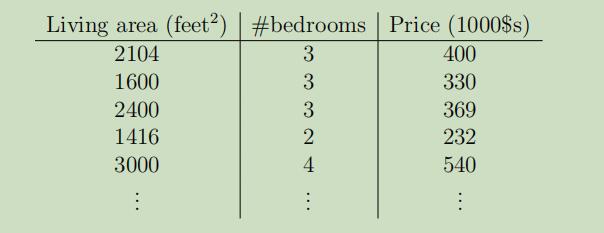 现在我们将采用特征x1(面积)和特征x2(卧室数量)来预测y(房屋价格)
现在我们将采用特征x1(面积)和特征x2(卧室数量)来预测y(房屋价格)
使用如下的线性函数来估计y:
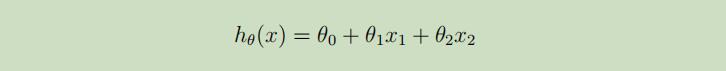
若在这里将x0设为1,并将x和θ表示成列向量,则上图中的假设函数可简写为:
 其中n表示输入变量的个数。
其中n表示输入变量的个数。
为了能 找到相应的参数θ,使第i个的h(x)和y的方差尽可能的小(即使第i个样本的估计值与实际值的误差尽可能小),定义 花费函数(cost function) 如下:
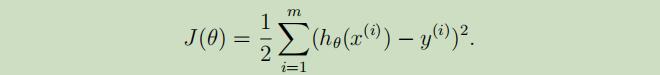 其中m是训练集样本总数,1/2是为了方便计算。
其中m是训练集样本总数,1/2是为了方便计算。
LMS algorithm
我们可以使用 梯度下降算法(gradient descent algorithm),来选择合适的θ从而使J(θ)最小化。梯度的方向就是函数在一个点 下降最快的方向。
在这里 初始化θ为0向量,得到θ的更新公式:
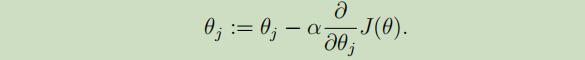
在这里给出上式详细的推导化简过程(假设m=1):
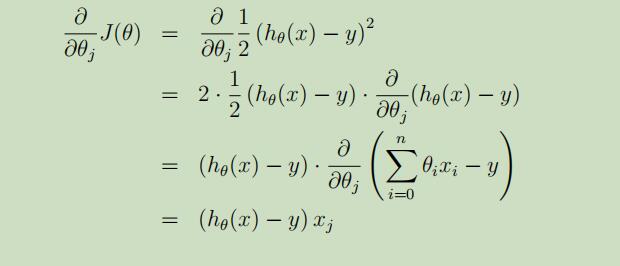
故,最终的更新公式(或LMS规则)如下:
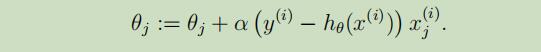
当只有一个训练集只有一个样本的时候,我们可以使用LMS规则,但是当一个训练集拥有不只一个样本时,我们有两种算法可以选择。
- 批量梯度下降(batch gradient descent)
对于每个θj,都要遍历整个训练集,当训练集规模较大时,运行很慢。
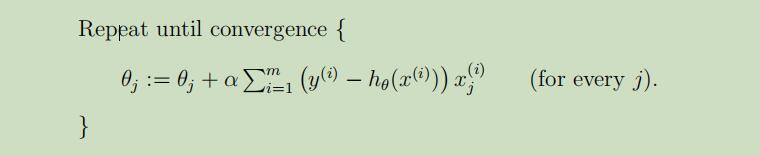 下图对拥有上面房屋价格例子的运行结果,通过获得的参数,拟合除了一条一次曲线。
下图对拥有上面房屋价格例子的运行结果,通过获得的参数,拟合除了一条一次曲线。
- 随机梯度下降(stochastic gradient descent)
不用每个参数遍历全部样本,即使它可能不会收敛到最小值,但是在实际中足够接近真正的最小值。因此随机梯度下降比批量梯度下降更常用。

矩阵偏导数(matrix derivatives)
对一个关于矩阵A的函数f(A)关于矩阵A求偏导,即求矩阵A所有分量的偏导,的公式如下:
 例子:给定二阶矩阵
例子:给定二阶矩阵 给定函数f(A)
给定函数f(A)
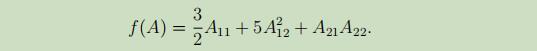 则f(A)关于A的偏导数为:
则f(A)关于A的偏导数为:
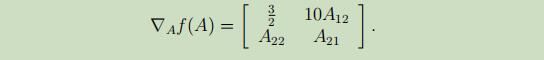
在这里列出些常用的线性代数知识点:
矩阵的迹(trace)记为如下:
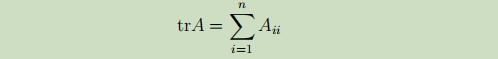
迹的几条性质如下:
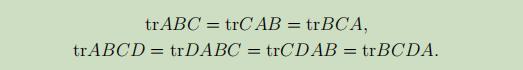
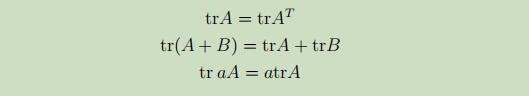
不加证明的给出下列常用矩阵偏导性质:
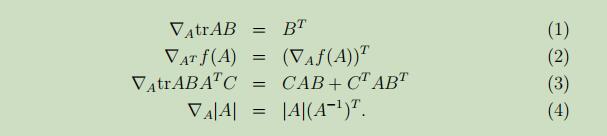
最小二乘
定义(m,n+1)的矩阵X如下(m个样本,n+1个变量):
 m维的目标变量的向量如下:
m维的目标变量的向量如下:
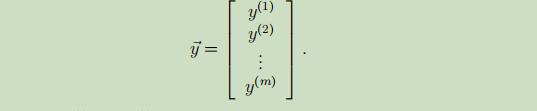 得到:
得到:

做其内积得到J(θ):
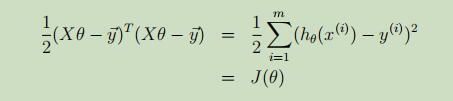
对J(θ)关于θ求导:
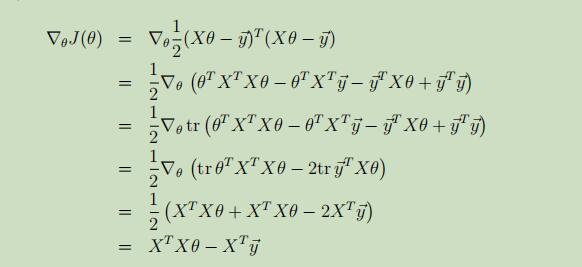
并令其=等0,得到normal equations
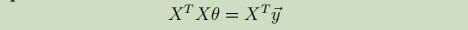
最终,得到不需要经过复杂的梯度计算的,仅使用矩阵运算的参数θ:
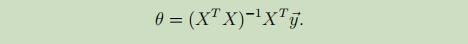
这就是最小二乘法。