网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/image/Stanford/cs229-notes1.pdf
Lecture 3 -Weighted Least Squares. Logistic Regression.
1. 局部加权线性回归（Locally weighted linear regression）
考虑之前的线性回归的例子，我们根据数据集拟合除了一条一次曲线，如下图1。现在，根据同样的数据集拟合一条二次曲线（ $y = θ_0 + θ_1x + θ_2x^2$），和六次曲线如下图。
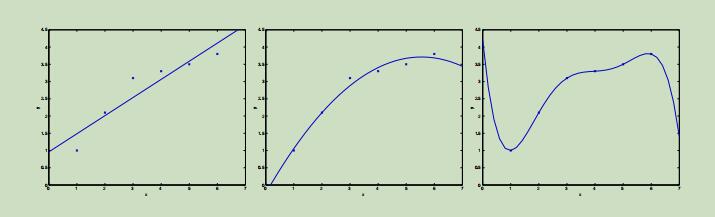
从这些曲线中，可以明显的看出二次曲线能更好的拟合提供的样本点。在一次曲线中有几个样本点离拟合曲线距离较远，未能充分利用样本点之间的关系，最后预测的结果会和真正的结果存在一定的误差，这称之为 欠拟合。在最右边的六次曲线中，曲线经过了所有的样本点，但是它并不能反映出正确价格的趋势，这称之为 过拟合。
在局部加权线性回归中，为了估计一个确定点的预测值，只使用其相邻的数据子集，并对其拟合一条曲线，通过这条曲线来预测该点的值。
在这里，我们将原先的线性回归算法修改如下：
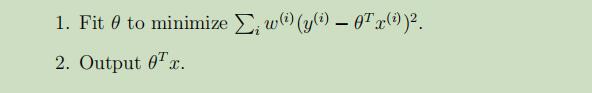
在这里，我们引入了 权值w(i)，如果对特定的i权值很大，就要选择θ使$(y^{(i)}-θ^Tx^{(i)})$尽可能的小。如果对于i的权值比较小，那么关于$(y^{(i)}-θ^Tx^{(i)})$的错误项就可以被很好地忽略。
常用的权值标准如下：
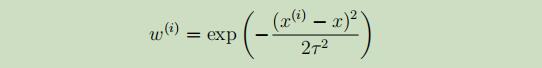
例如在给定的样本点如下图：
当xi距离给定的点x， 距离接近0时，wi的权值接近1，但是对于那些距离给定点 x距离较远的点，其权值会变得很小，其对线性回归最后的贡献也会变得很小。
故在局部加权线性回归中，通过拟合一组参数，来更多的关注于对临近点的精确拟合。
在权值的计算过程中，涉及一个参数τ，其代表权值下降的速率。如下图中，两个不同的τ对应的权值下降如下：
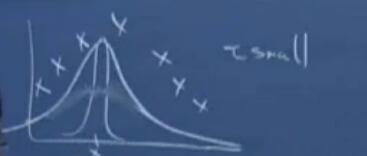
本例 中的 局部加权线性回归是一种 非参数算法（non-parametric algorithm），而 以前介绍的线性回归是一种 参数算法（parametric algorithm）。
参数算法： 拥有固定、有限的适合此数据集的参数θ，一旦我们通过学习算法拟合除了参数θ，并将其存储，在之后的预测中将不再需要原先的训练集。 非参数算法： 在未来的预测中需要在一直维持整个训练数据集，非参数可粗略的认为是，为了表示假设h而保持的样本的数量与训练集的规模成正比。
概率层面的解释
当我们面对一个回归问题的时候，思考为什么线性回归，和更确切的最小二乘 cost 函数J，是一个合理的选择？
现在假设目标变量和输入变量之间的关系如下等式：
其中,ε是未建模的影响因子或随机噪声，假设ε服从标准正态分布，且每个εi独立同分布，可以得到ε的密度函数如下:
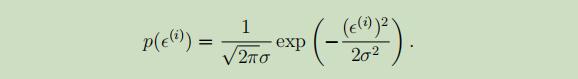
故，可以得到，给定变量x且以θ为参数的，y的概率密度函数为：
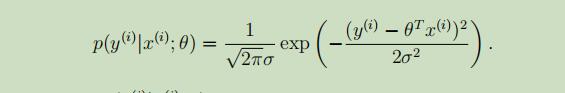或者可以写成变量y的分布：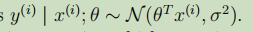
随后，得到参数θ的似然函数：
但，通常情况下，使用的是对数似然函数：
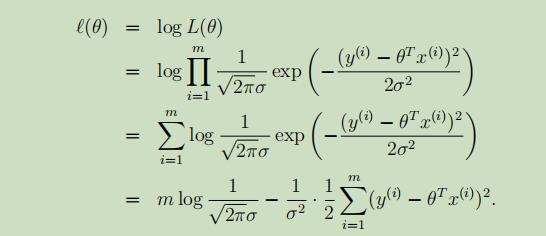
在上等式的右边，即是我们之前所定义的损失函数J(θ)，使L(θ)最大化的过程就是使等式右边的J(θ)最小化的过程。
总结：在前面的对数据集概率假设的前提下，最小二乘回归就是在做θ的极大似然估计。 需要注意的是，参数θ的最终选择不依赖于方差σ。
分类和回归
2.逻辑回归（logistic regression）
当变量是离散时，假设y只能为0或者1，这时在采用之前学习的线性回归来进行分类，结果就不会那么的好，甚至偏差很大。为了解决这个问题，我们将假设函数更改如下：
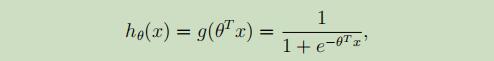其中，
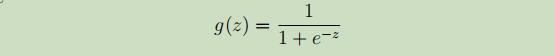被称为逻辑函数或sigmoid函数，其图像如下：
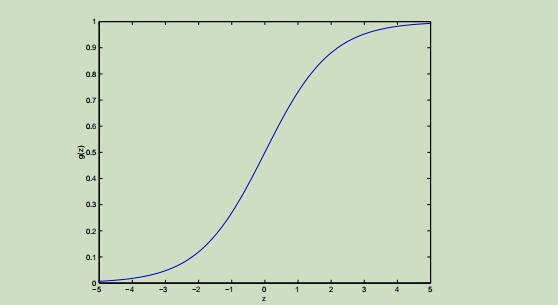
这样就可以将预测的结果映射到0-1范围之间了。
2.1损失函数
现在我们令在给定样本x时的预测值$\hat y$为： \(\hat y = P(y=1|x) = h_\theta(x)\)
当我们有一堆样本$\lbrace (x^{(1)},y^{(1)}),…,(x^{(m)},y^{(m)}) \rbrace$时，我们希望能够有$\hat{y}^{(i)} \approx y^{(i)}$，所以我们跟线性回归一样，写出单个样本的loss 函数： \(L(\hat y,y) = \frac {1}{2}(\hat y-y)^2\) 但是后面我们发现，这个损失函数非凸，求不得最优解。于是我们将损失函数更换如下： \(L(\hat y,y)=-\lbrace ylog\hat y+(1-y)log(1-\hat y) \rbrace\)
y的取值只能为1或0，显而易见该损失函数是凸函数。
并且注意，如果y=1，$L(\hat y,y) = -log\hat y$，最小化$L(\hat y,y)$，等同于最大化$\hat y （0<\hat y<1）$。
如果y=0，$L(\hat y,y)= -log(1-\hat y)$，最小化$L(\hat y,y)$，等同于最大化$\hat y （0<\hat y<1）$。
因此，这是一个十分合理的损失函数，我们就可以通过最小化整个样本的平均损失函数来学习参数：
\[\theta = argmin_\theta J(\theta) = argmin_\theta -\frac {1}{m} \sum _{i=1}^m \lbrace ylog\hat y+(1-y)log(1-\hat y) \rbrace\]2.2极大似然估计
之前我们已经学习了最小二乘回归可以用基于一系列假设的极大似然估计表示，那么在逻辑回归中，通过极大似然来选择合适的参数θ呢？
先进行如下假设：
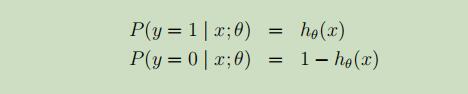
简写为：
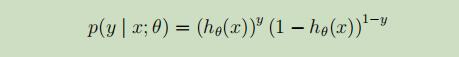假设m个样本之间是相互独立的，我们可以得到似然函数如下：
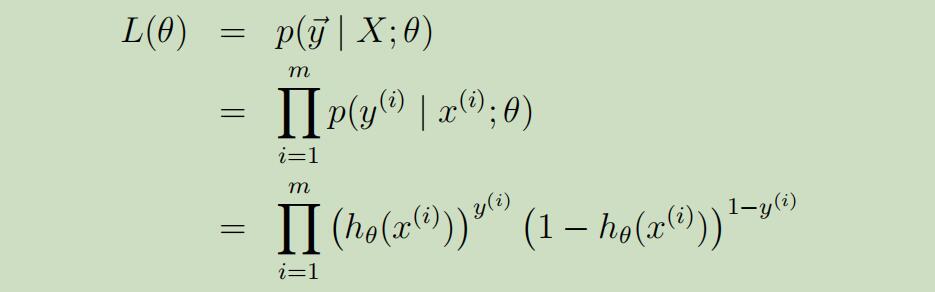其对数似然函数如下：
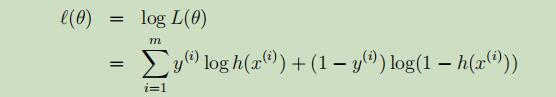其偏导如下：
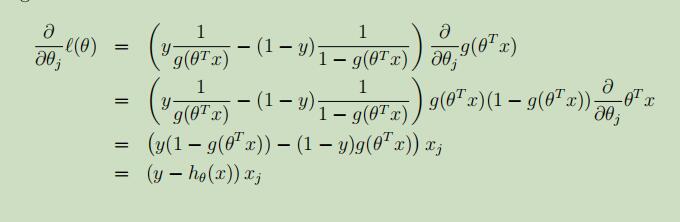
现在采用类似于之前讲过的随机梯度下降法，采用随机梯度上升法，来使得L(θ)的可能性达到最大。得到参数θ的更新公式如下：
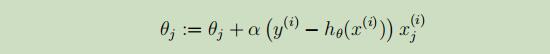
3.逻辑回归-神经网络模式
逻辑回归算法其实就是一个简单的网络，下面将介绍逻辑回归算法如何按照神经网络模式运行。
对于一个样本的逻辑回归可以转换为下图的形式：
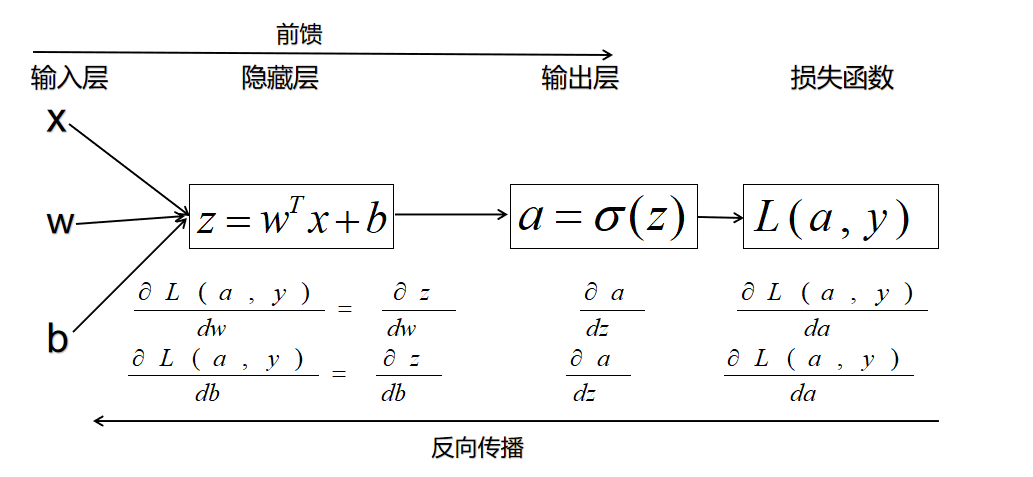
当有多个样本时，我们的前馈就变成了： Forward Propagation:
- You get X
- You compute $A = \sigma(w^T X + b) = (a^{(1)}, a^{(2)}, …, a^{(m-1)}, a^{(m)})$
- You calculate the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
反向传播所用到的更新公式为： \(\frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\) \(\frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\)
4.感知器算法（perceptron learning algorithm）
考虑修改逻辑回归方法，使其“强制”输出值为0或1或精确。为了达到这个目的，需要改变g的定义，使其成为这样的门限函数：
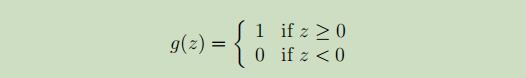使用和之前一样的假设函数h(x)，我们得到θ的更新公式：
这称之为感知器学习算法
