网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/image/Stanford/cs229-notes1.pdf
Lecture 4 -Netwon’s Method .Perceptron. Exponential Family. Generalized Linear Models.
Netwon’s Method
Netwon’s Method一种是不同于逻辑回归的算法，其目的仍是最大化$l(θ)$，但是在这里寻找的是另假设函数=0的点。下面介绍其算法思想：
如下面三幅图所示，首先确定一个点$θ_0$，之后在其对应函数点$f(θ_0)$做切线，记其切线与y=0的交点为$θ_1$，并进行迭代。
在迭代两次后的结果如图所示
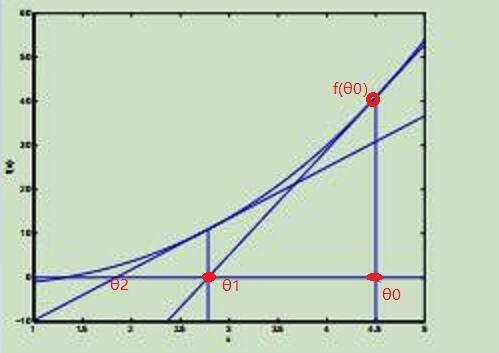
若迭代更多次，可以看出θ的值会越来越接近零点。
现只考虑$θ_0$的切线，其斜率可以表示为：
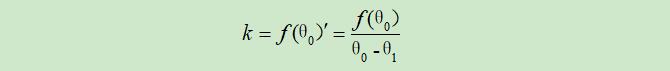从而可以得到$θ_1$的值：
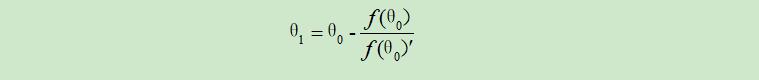故参数θ的更新公式为：
进行不断的迭代，最终可以得到假设函数$f(θ)$的一个 零点。这时如果设$f(θ)$是$l(θ)$的一阶导函数，那么$f(θ)$的零点即是似然函数$l(θ)$的极值点，从而达到最小或最大化一个函数的目的。且变化后的更新公式如下：
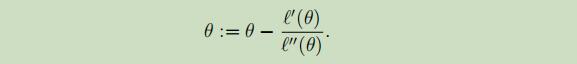
但是，在逻辑回归中，参数θ是一个向量，通过Newton-Raphson方法，可以将θ扩展到多维：
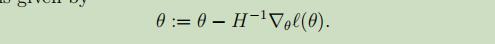
总结：一般来说，当采用的特征数目不是特别的大的时候，Newton方法会比梯度下降方法快一些，但是当特征数特别多的时候，n+1*n+1维的Hessian矩阵的逆将会需要特别大的计算量。
广义线性模型（GLM,Generalized Linear Models）
在此部分，将运用大量的概率论知识来解释GLM族中的模型如何导出并应用于回归和分类问题。
指数族（The exponential family）
当一类的分布属于指数族的时候，它可被写成如下的形式：
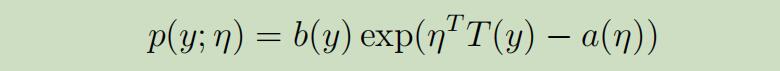$η$是自然参数；$T(y)$是充分统计量，常取$T(y)=y$；$α(η)$是对数划分函数，e$xp(-α(η))$能确保概率全部加起来等于1。
当我们固定T，a和b时，改变η时可以得到不同的指数分布。
例如，n=1时的伯努利分布（0-1分布）
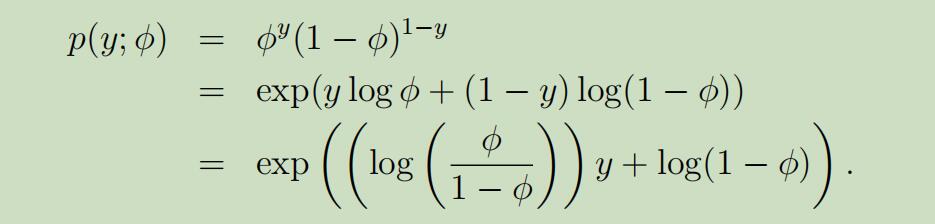
经过下图的变换，伯努利分布即可写成指数分布族的形式：
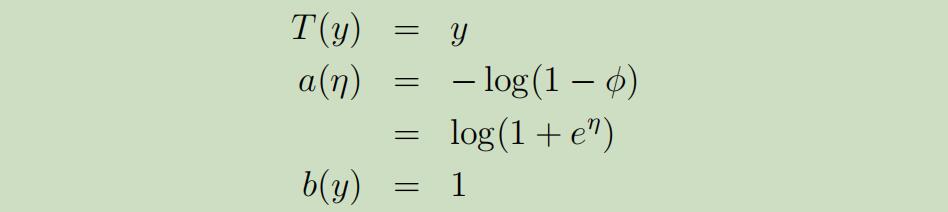
在这里呢，我们是将自然参数为，η = log(φ/(1 − φ)).但如果用η来表示φ，φ =1/(1 + e^−η),这就是我们在逻辑回归中所用的sigmoid函数！
同样，如果我们选择合适T，a和b，也可以将高斯分布（正态分布）也写成指数分布族的形式。
在线性回归中我们就介绍过，σ的选择对θ以及h(θ)没有影响，所以这里我们另σ=1.
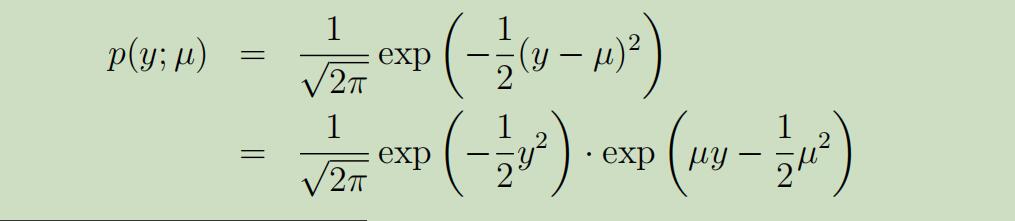经过下图的变换，正态分布即可写成指数分布族的形式：
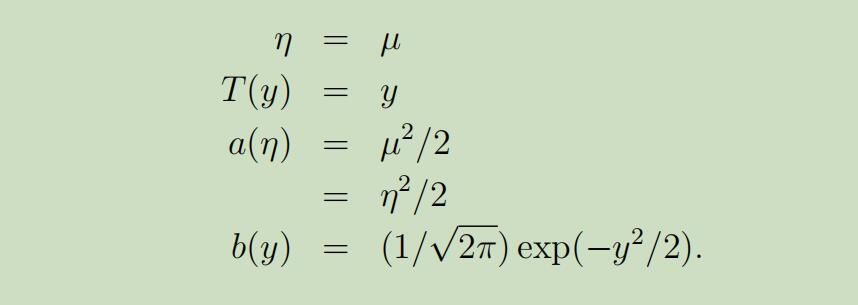
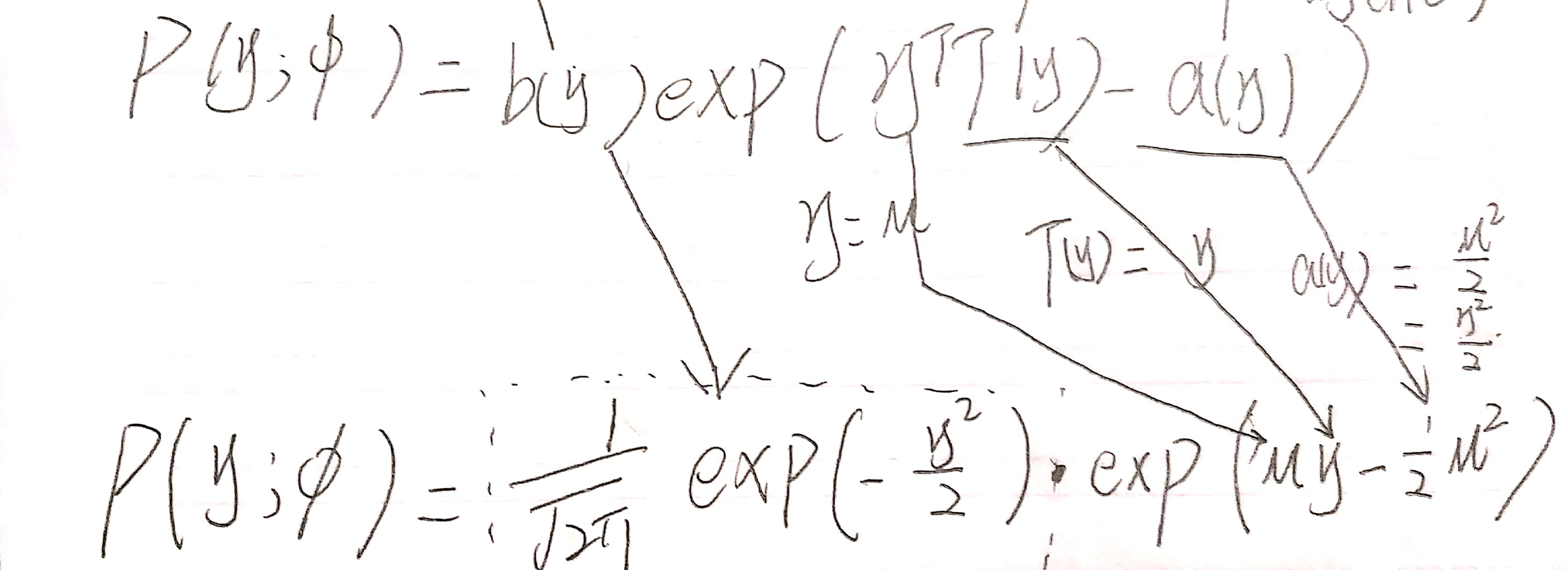
指数分布族的成员还有：多项式、泊松分布、伽马指数分布、贝塔-迪利克雷分布等。
构造GLMS(Generalized Linear Models.)
问题描述：
假设你想构建一个模型来估计在给定的任何时间内商店的访客人数y，这个模型基于特定的特征值如：促销、广告、天气、工作日等。已知泊松分布提供常用于访客的模型，但是我们该怎么建立一个能使用于我们问题的这个模型呢？
幸运的是，泊松分布属于指数分布族，所以我们可以对其应用GLM。在接下来，我们将描绘一种方法能用于为我们的问题来建立GLM模型。
为了能够对这个问题导出一个GLM模型，我们将做以下三个假设，在我们的模型中其关于给定x的条件分布y：
1. y | x; θ ∼ ExponentialFamily(η).
2. h(x) = E[y|x].
3. 自然参数η和输入x线性相关：η = θTx.（如果η是向量，那么 ηi = θiTx.）
这三种假设/设计选择将使我们能够派生出一种非常优雅的学习算法，即GLMS，它们具有许多可取的特性，例如易学性。此外，结果模型对于模拟y上的不同类型的分布通常是非常有效的；例如，我们将在下面说明的逻辑回归和普通最小二乘都可以是派生为GLMS。
普通最小二乘
普通最小二乘是GLM族模型的一个特殊的例子，考虑设置目标变量y（在GLM术语中称为响应变量）为连续的，并使在给定x条件下的分布y服从正态分布N(µ, σ2). 利用先前学习的知识，使ExponentialF amily(η)成为正态分布。
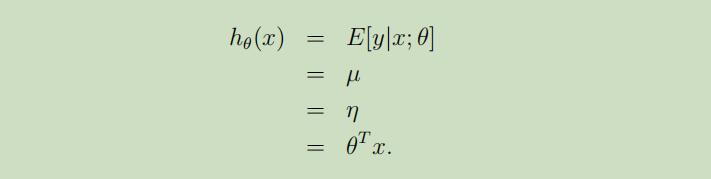
第一个等式，即假设1；第二个等式，为正态分布性质；第三个等式，为之前正态表示为指数分布族时获得的性质；第四个等式，即假设3
逻辑回归（logistics regression）
现在我们来考虑二分类问题，即$y ∈ \lbrace 0, 1 \rbrace$。自然，应当选择伯努利分布来对给定x下的条件分布y建模。这之前将伯努利分布用指数分布族来表示时，我们获得了$\phi = 1/(1 + e^{−η})$。与普通最小二乘类似，使ExponentialF amily(η)成为伯努利分布。
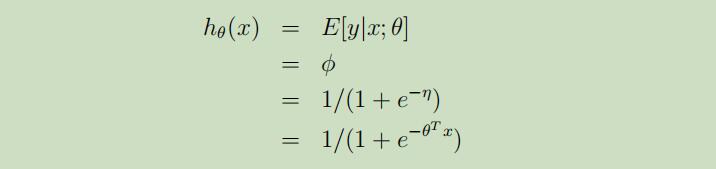所以，这就为我们在之前逻辑回归课程中的假设函数从何而来？ 这个问题给出了答案：一旦我们假设给定x下的条件分布y是伯努利分布，这个假设函数就可以从GLM的定义和指数分布族中导出。
在这里介绍些术语： 以$η$为参数的函数$g(η)$，令其等于分布的均值 $g(η) = E[T(y); η]$，$g(η)$被称为权值响应函数，它的逆被称为权值连接函数。 因此，在高斯分布中，权值相应函数就是identify function；在伯努利分布中，权值响应函数就是logistic function.
Softmax Regression
当面对多分类问题 时，即$y ∈\lbrace 1, 2, . . . , k\rbrace$且离散，我们需要使用多项式分布来进行建模。 在将多项式表达成指数分布族过程中，首先理解以下符号：
φ1,..., φk−1 定义为产生每种结果的概率，φi = p(y = i; φ)且 φk = 1 −φ（1至k）。
指示函数1{·}，定义为1{True} = 1, 1{False} = 0。
然后定义$T(y)$如下：
注意，这里T(y)!=y，且为k-1维向量。
$T(y)$和$y$的关系也可以表示为：$T(y)_i = 1\lbrace y = i\rbrace$ 还可以获得$E[T(y)_i] = P(y=i) = \phi _i$
随后，将其表示为指数分布族：
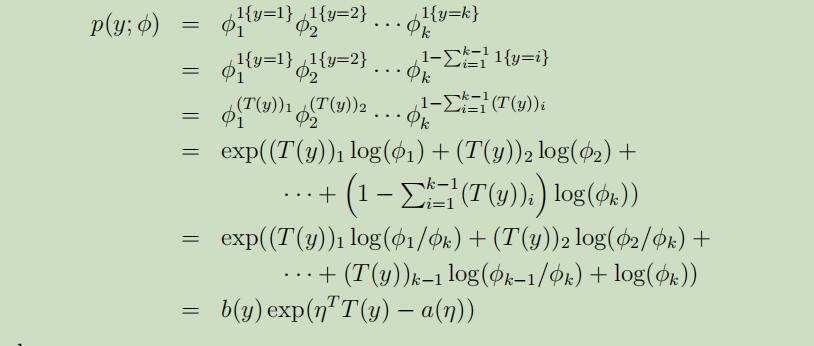
其中，
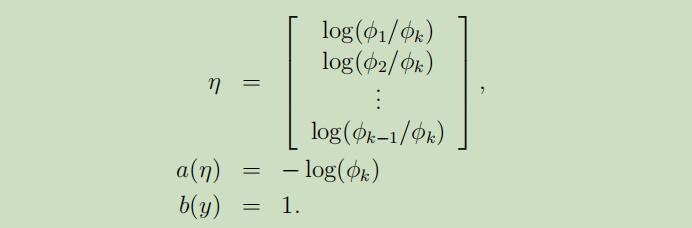
以上这些步骤完成了多项式表示成指数分布族形式。
下面来
得到的连接函数 函数如下：
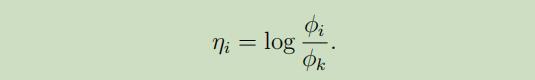连接函数的逆，即是响应函数，因此对连接函数求逆：
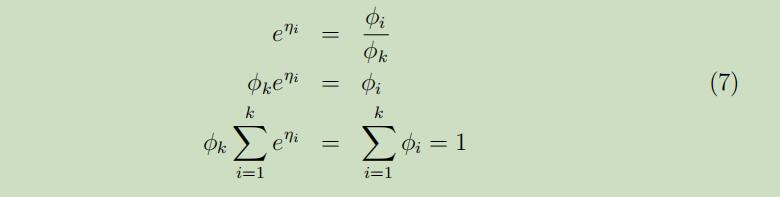从第三个等式中，可以得到
将其带回到第二个等式中，可以得到响应函数 ：
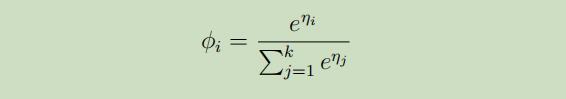这个函数也被称作为softmax 函数 。
为了完成我们的模型，利用假设3，并定义$θ_k = 0$,可以得到给定x下的条件分布y为：
运用这个模型去解决多分类问题的模型叫做softmax regression ，这是广义化的逻辑回归。
我们的假设函数将会输出 ：
输出结果，就是每一分类结果的概率。
最后 ，向原始的逻辑回归和最小二乘中，寻找出合适的参数θ，我们写出本例的对数似然函数 ：
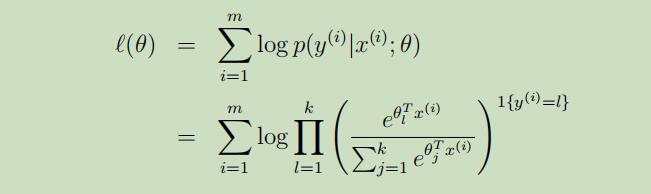我们可以使用梯度上升或者牛顿方法 来寻找到使似然函数最大的参数θ。
