转载请注明本博客地址https://yunlongs.cn/2019/04/26/NE-Node2vec/
Node2vec算法原理深度研究
1. 算法介绍
很多网络分析任务都会涉及到节点和边的预测，比如在典型的节点分类任务中，我们会着重关注于预测网络中的节点最可能拥有的标签；在链接预测任务中，我们希望能够预测网络中的一对节点是否有一条相互连接的边。任何监督类机器学习算法都需要一组信息量大、有偏重和独立的特征，在网络预测问题中这意味着必须要为节点和边建立特征向量表示，典型的解决方法是手工提取特征，但这种方法费力且不能在不同的预测任务中得到泛化。
一个相对的解决方案是通过解决一个优化问题来学习特征表示，目标函数的选择将涉及计算效率和预测准确性，因此如何定义一个优化目标函数成为特征学习的挑战。一方面人们可以去直接寻找一个能优化预测性能的特征表示，虽然这种带监督的方法虽然拥有很好的准确性，但是当需要估计的参数数量很大时这将导致很高的训练时间复杂度。另一方面，目标函数可以被定义为和预测任务独立并且表示可以完全通过无监督方式来进行学习，这可以通过精心设计一个目标函数来使优化上的计算变得更有效率，而且这些与任务相独立的特征能够与针对特定任务获得的特征达到类似的准确率。
然而当前的技术并不能定义和优化一个网络中可扩展无监督特征学习所需要的目标函数。相对的，我们可以设计一种力图去保留节点局部范围内邻居信息的目标函数，这个目标函数可以使用随机梯度下降算法在单隐藏层的前馈神经网络进行有效的优化。Node2vec作者特别指出网络中的节点可以组织在一起可以形成这些节点所属社区的形式，例如在图8中，节点u和s1-s4共同属于一个相同的节点社区，节点u和s6虽然属于两个不同的社区，但是在结构上都扮演着相同的中心节点角色。真实世界中的网络通常由这些相同的结构复合在一起组成，因此为了能够使特征学习算法在不同的领域和预测任务中得到泛化，作者提出了Node2vec算法设计中所要遵循的两条准则：
- 通过嵌入同一社区节点学习得到的表示能够足够的接近。
- 对在网络拓扑扮演者相同角色的节点进行嵌入时获得的表示应当相似。
Node2vec算法同Deepwalk具有很高的相似度，都是借助自然语言处理中的词嵌入技术，将对网络中进行游走获得的序列当作特出的语料，使用随机梯度下降算法来优化一个基于图的目标函数。其与Deepwalk算法的不同之处主要在于Node2vec采用二阶随机游走，如图8所示二阶随机游走既可以向远处游走从而描绘出网络的宏观特征，又可以在局部游走从而保留节点的社区信息，故此方法返回的特征表示最大可能的保留了节点在特征空间中的网络邻居信息。另一点不同在于Node2vec将基于节点的预测任务扩展到了基于边的预测任务。
2. Node2vec游走
Node2vec在Deepwalk的关于图的定义基础上添加了邻居的定义，定义$N_{S}(u) \subset V$为节点u在邻居取样策略S下的网络邻居列表。我们可以把源节点的邻居取样问题看做为局部搜索的一种形式，限定邻居集合$N_{S}(u)$的大小为k个节点，作者给出了两种生成k个节点的邻居集合$N_{S}(u)$的极端取样策略：
- 广度优先取样(BFS)：邻居$N_{S}(u)$仅限于源节点u的近邻节点，如图8中的s1，s2，s3，其中k=3。
- 深度优先取样(DFS)： 邻居$N_{S}(u)$由从源节点u开始距离不断增加的节点序列组成，如图8中的s4，s5，s6。
对这两种在极端情况下的取样策略在搜索空间的探索，能对之后的学习表示带来意想不到的影响。在实际生活中，网络节点的预测任务通常在如下两种相似度上进行交替：同质性和结构等价 。在假设满足同质性时，相互连接并且属于相同网络社区的节点的表示向量应当相似；在假设满足结构等价时，拥有相同网络结构的节点的表示向量也应当相似。我们可以观察到BFS和DFS策略在产生能满足以上两种性质的表示时起到了重要的作用，由BFS策略进行采样获得的邻居通常都具有结构上的相似性，而DFS正好相反，由DFS策略进行采样获得的邻居能更好的满足网络的同质性。
作者根据BFS和DFS的思想设计了一种灵活的带有偏重的随机游走策略，使BFS和DFS能够平滑地融入此策略中。给定一个源节点u，要进行步长为l的随机游走，$c_i$表示游走序列中第i个节点且$c_{0}=u$，节点v到x的转移概率，Z为归一化常量，节点$c_i$由以下分布产生：
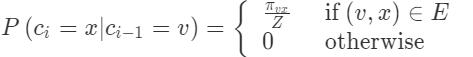定义由参数p和参数q引导的二阶随机游走如下：如图假设随机游走序列由节点t经过了边(t,v)，现在要决定节点v的下一步游走方向，所以需要评估出边(v,x)上的转移概率$\pi_{v x}$，并将转移概率最大的边作为下一步游走的方向，设边(v,x)上的权值为$w_{v x}$，则转移概率
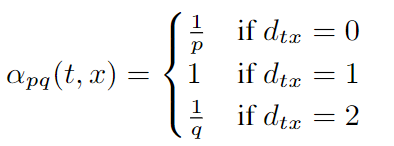
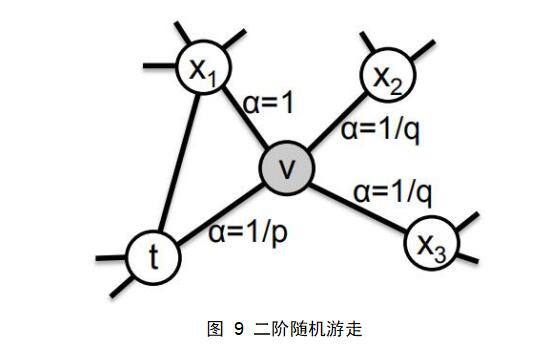从直观上可以看出，参数p和q控制的是游走序列向外探索和离开原来邻居节点的速率，特别的是当p=q=1时，Node2vec的二阶随机游走的采样策略与Deepwak的随机游走策略一致。下面详解参数p和参数q在二阶随机游走所起到的作用：
返回参数p： 参数p控制在随机游走立即重新访问一个节点的可能性。当p取值很大时$(p>\max (q, 1))$，控制往回游走的概率就会相对较小，这样重新对已经访问过的进行访问的可能性就会更小，这样的策略可以鼓励往外进行探索并且避免跳到已访问节点造成的冗余。另一方面，若当p的值很小$(p<\min (q, 1))$时，游走序列将会很大的概率一直围绕源节点u的邻居进行采样，这样十分有益于描述一个节点与其邻居节点之间的关系。
进出参数q： 参数q可以在游走路径的搜索过程中区分“向内”和“向外”的节点。当参数q>1时，随机游走就会更偏向于朝向那些之前访问过节点很近的节点，这样的策略有助于我们获得源节点u的局部视图，在局部范围内，这种策略更像是BFS。相反的，如果q<1，那么游走序列会离之前访问过的点越来越远，这种向外探索的策略更像是DFS。
3. 算法设计
Node2vec在学习表示过程中仍然是借用自然语言处理中的词嵌入技术中的Skip-gram模型，但不同的是这里没有继续使用基于Hierarchical Softmax的Skip-gram模型，而是为了提高计算效率，使用的是基于Negative sampling的Skip-gram模型，在获得Node2vec随机游走序列后，将需要进行优化的目标函数设定为：
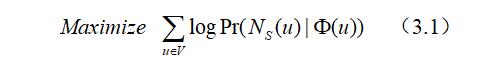为了能够使目标函数更容易地处理，这里需要引入两条假设：
- 条件独立：假设我们所取样得到的邻居中每个节点之间都是相互独立的，这样就可以将式（3.1）中的概率分解为：
- 特征空间中的对称性：假设节点t是节点u的邻居，那么u同样也是t的邻居，将这种关系映射到特征空间中那就是，节点u对节点t的影响和节点t对节点u的影响是相同的。基于这种关系，可以将公式（3.2）中的概率进一步展开为：
基于以上两点假设，我们可以将目标函数（3.1）转化为：
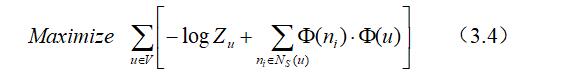其中$Z_{u}=\sum_{v \in V} \exp (\Phi(u) \cdot \Phi(v))$在大规模网络中计算量很大，作者使用负采样的方法来得到$Z_{u}$的近似值，使用随机梯度下降算法优化此目标函数，在优化过程中即可得到节点的嵌入表示。
4. 嵌入向量产生过程
Node2vec算法是将获得的游走序列当作一种特殊的语料，使用基于Negative sampling的Skip-gram模型来产生嵌入向量，接下来将介绍这种模型产生词向量的过程。
给定词w的上下文Context(w)，能够与Context(w)相对应的词（中心词w）称之为正样本，通过负采样得到的neg个不同于w的中心词$w i, i=1,2,3 \ldots .$ neg称之为Context(w)的负样本。因为从样本中进行采样，获得的只能是Context(w)的正样本或者负样本，故采样也可以看作是进行一次二元逻辑回归，因此我们的正样本应当期望满足：
我们的负样本应当期望满足：
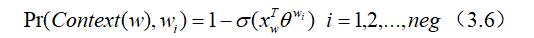我们期望最大化的表达式为：
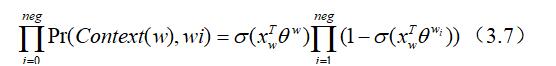使用随机梯度下降算法可得参数Xw的更新公式为：
在进行负样本采样时所使用的负采样算法是按照如下方法进行的：假设预料中不同词的个数为|V|个，将每个词的长度设置为：该词在语料中出现过的次数的四分之三次幂/语料中每个词出现次数的四分之三幂的合，如式（3.9）。
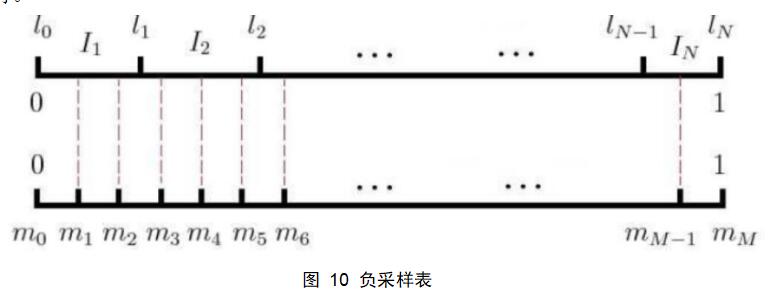故基于Negative sampling的Skip-gram模型产生词向量的流程如下：
5. Node2vec算法流程
可以注意到算法2中在选取游走序列下一个节点时使用了Alias取样方法，这里就不展开进行叙述，其作用为按照每条边的转移概率选取相对应的节点。
6.OpenNE中Node2vec算法流程
在OpenNE中Node2vec算法的实现中，算法大体也可分为两部分：Node2vec算法框架与游走序列的产生。在算法最开始进行的预处理转移概率图G中，其实并没有直接对图G进行操作，而是分别计算出仅根据边的权值计算出的每个节点的转移概率alias节点取样表，和根据p，q进行导向控制的每条边的alias边取样表。在游走的初始阶段，游走序列中仅有起始节点，还未形成游走路径，这时参数p，q失去了其作用，故仅按照此节点所连边的权值来使用alias方法对下个节点采样；在经历过一次游走后，就已经形成了游走路径，故此后按照alias方法来对参数p，q预处理后的边进行采样，添加到游走路径中。
另外值得一提的是，在OpenNE中Deepwalk算法的实现是在Node2vec算法内完成的，当参数p,q的值均为1时，Node2vec的二阶随机游走就变成了Deepwalk的随机游走，Deepwalk的随机游走也变成了在p=q=1情况下的Node2vec二阶随机游走。
算法源码解析见OpenNe源码解析之Node2vec
