转载请注明本博客地址https://yunlongs.cn/2019/04/28/NE-LINE/
LINE算法原理深度研究
1. 算法介绍
大规模信息网络通常由上百万及上亿个节点组成，如何对大规模信息网络进行分析一直是工业届和学术界聚焦的热点，LINE算法的全称为 Large-scale Information Network Embedding，其目的就在于解决如何有效的将大规模信息网络嵌入到低维向量中，这种低维的嵌入具有可视化、节点分类、链接预测、推荐系统等多方面的应用场景。
LINE算法的发布时间为2015年，在此之前也有其他的图嵌入算法如MDS、IsoMap、Laplacian eigenmap，但这些算法只有在较小规模的网络中能展现出很好的性能，还有一小部分针对大规模网络嵌入的方法，但是这些方法要不就是间接完成对网络的嵌入，不是针对网络拓扑而设计的，要不就是针对网络嵌入缺少精心设计的目标函数。
LINE算法的出现很好的解决了上述的问题，并且LINE算法还能处理各种类型的网络，如无向图、有向图、加权图等，其在优化目标函数的过程中还能保留网络结构的全局特征和局部特征。LINE算法的出现比Node2vec算法早些，故其作者在一阶相似度已经不足以充分的概括网络结构特征时首次提出了二阶相似度的概念。
如图11很好的诠释了信息网络中的一阶相似度与二阶相似度的概念，当在连接节点6和节点7的边上的权值很大时，节点6和节点7就会有很大的一阶相似度，故这两个节点在特征空间的表示会十分相似；节点5和节点6虽然没有直接相连，但是节点5和节点6拥有共同的邻居，因此这两个节点拥有很高的二阶相似度，在特征空间内的表示也会十分接近。
LINE算法正是通过精心设计一个目标函数来保留网络中的一阶相似性和二阶相似性。同时，在针对大规模网络的优化中，随机梯度下降算法的使用受到了限制，因为在这种规模的网络中，边的权值变化的范围很大，在优化的过程中这些边的权值会乘以梯度，这就造成了梯度大范围的波动，被作者称之为梯度爆炸。为了解决随机梯度下降算法在大规模网络嵌入中的的局限性，作者提出了一种新颖的边采样算法，在保留目标函数不变的同时还能使梯度不再受到边权重的影响。
2. 算法设计
算法的建模主要是针对节点的一阶相似度和二阶相似度来进行建模。
首先讲述一阶相似性的建模过程：一阶相似性主要用来描述网络中两个直接相连节点之间的相似性，两个节点直接所连接的边的权重就代表着两个节点一阶相似性的强弱，对于每条无向边$(i, j)$，我们定义节点$v_i$和节点$v_j$的联合概率如下：
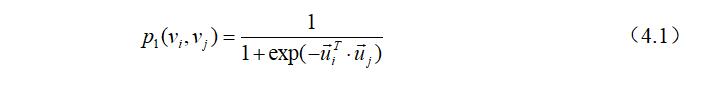其中$\vec u_i \in R^d$是节点$v_i$的低维向量表示，公式（4.1）定义了在特征空间下两个节点的分布，这种分布的经验概率可以被定义为如下：
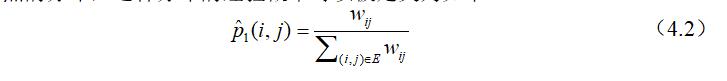易发现此分布的经验概率为节点$v_i$和节点$v_j$边权值在所有边权值之和所占的权重，为了能够保留异界相似性，目标函数被设计如下：
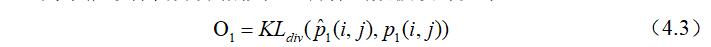公式（4.3）设计的目标是缩小两个分布之间的距离，使两个分布之间的差异性尽可能的小，尽可能的相似，通过不断的拉近一阶相似性的真实分布与经验分布之间的距离，最后达到两者的均衡，使得一阶相似性的损失尽可能的小。两个分布之间的差异性可以用KL-散度来进行表示，带入公式（4.3）中可以得到最终的一阶相似性目标函数：
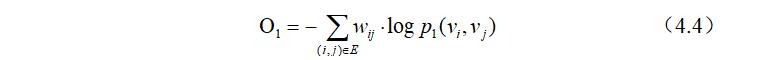通过对目标函数（4.4）进行最小化，我们可以得到每个节点保留了一阶相似性的向量表示${\vec u_i}_ {i=1 \ldots|V|}$。
下面讲述二阶相似性的建模过程：二阶相似性假设那些具有相同邻居节点的在特征上较为相似，两个节点拥有共同的邻居节点越多，其二阶相似性就越高。这此算法中，每个节点它本身具有两种角色：节点它自己和其他节点的邻居。当其作为节点自身时，节点$v_i$的向量表示为$\vec u_ i$；当其作为其他节点的邻居节点时，节点$v_i$的向量表示为$\vec{u}_ {i}^{\prime}$。对于每条有向边$(i, j)$，定义$v_i$在$v_j$下的条件概率为：
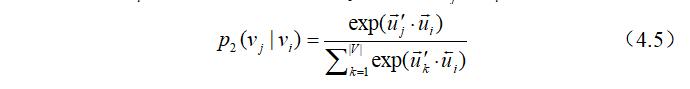公式（4.5）实际上是定义了$p_ {2}(\cdot | v_ i)$对于所有上下文的条件分布，为了能够保留二阶相似性，我们需要把上下文条件分布$p_{2}(\cdot | v_ {i})$和其经验分布$\hat p_2 (\cdot | v_i)$之间的距离尽可能的小，这里定义其经验分布$\hat p_{2}(\cdot | v_ {i})$为：
其中$d_i$为节点$v_i$所有的出度之和，可以得到二阶相似性的目标函数为：
因为每个节点在网络中的重要性程度是不同的，故引入$\lambda_ {i}=d_ {i}$用来评估一个节点在网络中的重要性，两分布之间的距离仍然使用KL-散度来表示，故可得最终的二阶相似性目标函数：
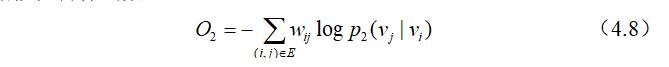通过对目标函数（4.8）进行最小化，对$\lbrace \overrightarrow{\mathcal{U}}_ i\rbrace _ {i=1 \ldots|V|}$和$\lbrace \vec u_ {i}^{\prime}\rbrace _ {i=1 \ldots|V|}$进行学习，我们可以得到每个节点$v_ i$对应的向量表示$\vec{u}_ {i}$。
3. 嵌入向量产生过程
二阶相似性目标函数（4.8）要计算出所有节点的条件概率$p_{2}(\cdot | v_ {i})$并进行求和，优化此目标函数时将会耗费巨大的计算量，为了解决这个问题，作者采用了负采样的方法，根据每个边$(i, j)$的一些噪声分布对多个负边进行采样。对于每个边所采用的目标函数如下：
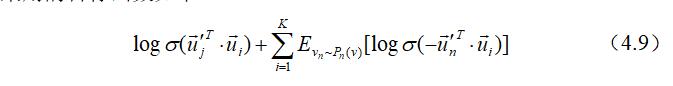式（4.9）的第一部分是对可见边进行建模，第二部分是对由噪声分布提取的负边进行建模，K为负边的数目，$P n(v) \propto d_{v}^{3 / 4}$。
LINE算法采用异步随机梯度下降(ASGD)算法来优化公式（4.9），每一步ASGD算法都会对边进行小批量采样，并更新参数，设采样的边为$(i, j)$，节点$v_i$的嵌入向量$\vec{u}_ {i}$所对应的梯度为：
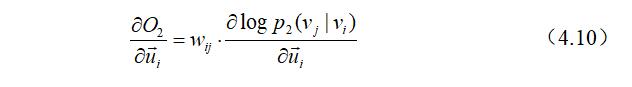从式（4.10）中观察到，梯度将会乘以边的权值，而大规模信息网络中存在数百万的边，其权值有可能非常小（比如1），也可能非常大（比如1000），这将导致嵌入向量$\vec{u}_ {i}$所对应的梯度可能特别的大，或者特别的小，这就导致很难去寻找一个很好的学习速率来进行学习。
作者提出了分解权值和边采样思想来解决梯度问题，分解权值即为将权值为w的边分解为w条边，这样每条边的权值就都为1，不存在梯度跳跃问题；变采样，即使用Alias取样方法按照每条边所对应的的概率对边进行采样，这样能够有效的避免分解权值造成的存储问题，并且还能使目标函数仍然保持不变。
在使用ASGD算法对式（4.4）和（4.9）优化可以分别得到保留有一阶相似性的嵌入向量u1和保留有二阶相似性的嵌入向量u2，将嵌入向量u1和u2相连接就可以得到同时保留一阶相似性和二阶相似性的嵌入向量。
4. LINE算法流程
5. OpenNE中LINE算法流程
源码解析见OpenNe源码解析之LINE
