网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes4.pdf
Lecture 9 - Learning Theory
1.偏差/方差 平衡（Bias/variance tradeoff）
当我们之前讨论线性回归时，我们曾经讨论过简单模型“$y=\theta_{0}+\theta_{1} x$”和更复杂模型“$y=\theta_{0}+\theta_{1} x+\cdots \theta_{5} x^{5}$”的例子，如下：
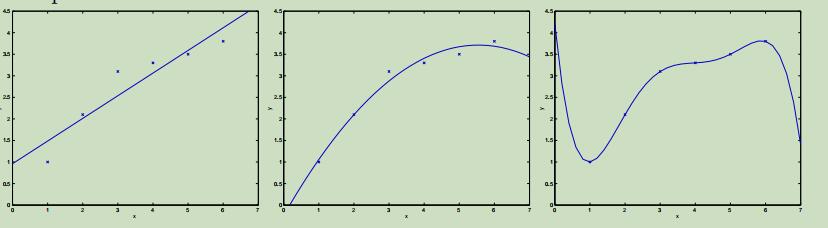在我们使用一阶的模型不足以描绘数据属性时，我们使用五阶建立的模型也不会是很好。即使五阶的模型能够很好的在此训练集中来预测y，但是五阶的模型却不能很好泛化地去预测其他的样本。假设的泛化误差（将严格地说是正确的）是它不一定在这里训练集中的例子上体现的预期误差。
图中左边和右边的模型都有着很大的泛化误差，但是他们造成泛化误差的类型是不同的。如果熟练集y与x之间的关系不是线性的，那么我们即使对一个大规模训练集拟合一个线性模型，它将不会很精确的捕获数据集中的结构。即使我们将其拟合到很大的数据集中，在这里我们可以把预期的泛化误差定义为偏差（bias）。因此对于这个问题来说，我们的模型具有很大的偏差，或者可以说模型欠拟合。
在右边的图中，我们成功的根据我们的小的、有限的数据集拟合出了数据的模式，但是用这个5阶的多项式去预测关于更多的y与x的关系将会有很大的风险，这样拟合的模型具有很大的偶然性。通过对这个训练集拟合出这个“不符合数据特征”的模式，我们可以称这个模型具有很大的泛化误差，这本例中我们可以称这个模型具有很大的方差。
通常，我们需要在偏差和方差之间寻找一种平衡，如果我们的模型过于简单并且有很少的参数，那么它可能有很大的偏差（但是方差很小）；如果我们的模型过于复杂并且有很多的参数，那么它可能有很大的方差（但是偏差很小）。这图中的例子中，对数据拟合一个二次函数相对于其他两个是最好的。
2.预备知识
为了能够最好的根据不同的设置来应用不同的算法，我们将会对以下几个问题进行探讨并寻求答案：
- 我们能否将前面提及的偏差和方差折中给正式化？ 这也将最终引领我们去讨论模型选择方法，例如自动选择几阶的多项式来拟合数据集。
- 在机器学习中我们真正关心的是泛化误差，但是大多数学习算法都是根据当前的数据集来拟合模型。为什么在训练集上表现的很好这还能告诉我们有泛化误差呢？更明确些，就是我们可以把训练集上的误差和泛化误差联系在一起吗？
- 实际上证明学习算法将会工作的很好这有什么限制条件吗？
首先介绍两个有用的公理：
- （联合概率上界）：$P(A_{1} \cup \cdots \cup A_{k}) \leq P(A_{1})+\ldots+P(A_{k})$
- （Hoeffding 不等式）：$Z_{1}, \dots, Z_{m}$都是服从二元伯努利分布的独立同分布的随机变量，例如$P(Z_{i}=1)=\phi$，$P(Z_{i}=0)=1-\phi$。现在令$\hat{\phi}=(1 / m) \sum_{i=1}^{m} Z_{i}$，并且任何$\gamma>0$都是固定的。可以得到：
这个定理（在学习原理中也被称为Chernoff bound）告诉我们如果采用$\hat{\phi}$来估计$\phi$，即使当m很大时，其和$\phi$的真实值相差很大的概率会很小。
我们使用二分类问题$y \in \lbrace 0,1\rbrace$来简化我们的探索过程，注意我们可以将其泛化到其他问题中，包过回归和多分类问题。 假设给定大小为m的训练集
$S=\lbrace (x^{(i)},y^{(i)});i=1,…,m \rbrace$，训练样本$(x^{(i)}, y^{(i)})$是服从概率分布$\mathcal{D}$的独立同分布样本，我们定义假设h的训练误差（在学习原理中也被称为经验风险或经验错误）为：
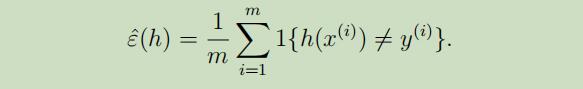
我们可以标记$\hatε_S(h)$为对于训练集S的训练误差。我们也可以定义泛化误差为：
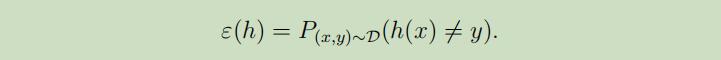对于线性分类问题，$h_θ(x)=1\lbrace θ^{T} x \geq 0\rbrace$，有什么合理的方式来拟合参数θ呢？一种方法是试图最小化训练误差，取
\(\hat{\theta}=\arg \min _{\theta} \hat{\varepsilon}(h_{\theta})\)
我们把这个过程叫做经验风险最小化（ERM），并且学习算法得到的假设输出为$\hat{h}=h_{\hat{\theta}}$。我们可以把ERM看待为最基础的学习算法，并且这也是我们将要研究的中心。（类似于逻辑回归之类的算法都可以被视作为ERM的近似算法）
在我们对学习原理的学习过程中，适当的抽象化将是十分有效的。在这里，我们将学习算法所使用的假设类H定义为它所考虑的所有分类器的集合。因此，对于线性分类问题， \(\mathcal{H}=\lbrace h_{\theta} : h_{\theta}(x)=1\lbrace \theta^{T} x \geq 0\rbrace, \theta \in \mathbb{R}^{n+1}\rbrace\)是在$\mathcal{X}$（输入域）上所有分类器的集合，其决策界限是线性的。更宽泛的说，如果我们在研究神经网络，那么我们可以让$\mathcal{H}$为一些神经网络结构可以表示的所有分类器。
ERM现在可以被认为是对函数$\mathcal{H}$类的最小化，其中学习算法采用如下假设：
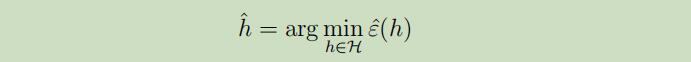
3. 有限H的例子
首先考虑如下学习问题：假设我们有一个有k个假设组成的有限假设类$\mathcal{H}=\lbrace h_{1}, \dots, h_{k}\rbrace$，这样$\mathcal{H}$就成了有k个从$\mathcal{X}$到{0,1}的函数映射集合，并且ERM选择$\hat{h}$为这些k个函数中有最小训练误差的那个。
我们想要对泛化误差$\hat{h}$做出保证，我们可以把策略分为两部分：
- 我们首先要展示出对于所有的h来说，$\hat{\varepsilon}(h)$是${\varepsilon}(h)$的可靠估计。
- $\hat{\varepsilon}(h)$的泛化误差有上界。
对任何的$h_{i} \in \mathcal{H}$取值都固定。考虑如下伯努利随机变量$Z$，从$D$中取样$(x, y) \sim \mathcal{D}$，因为我们的训练集是服从$\mathcal{D}, Z$的独立同分布样本，可以定义$Z_j=1\lbrace h_{i}(x^{(j)}) \neq y^{(j)}\rbrace$.
我们可以看出对随机的一个样本$\varepsilon(h)$错误分类的概率实际上就是$Z_j$的预期值。更多的，训练误差可以被写为：
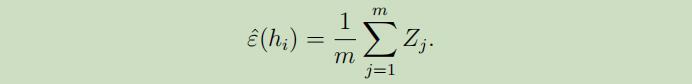
在这里我们可以应用Hoeffding 不等式，得到：
可以看出来，当m很大的时候，对于特别的的$h_i$其训练误差将会很大概率地与泛化误差接近；但是我们不仅仅想要确保只对一个特指的$h_i$满足$\varepsilon(h)$和$\hat{\varepsilon}(h)$很接近，我们想要做到的是，正别对于所有的$h \in \mathcal{H}$都同时满足这个规律。为了做到这样，我们现在令事件$A_i$表示$|\varepsilon(h_{i})-\hat{\varepsilon}(h_{i})|>\gamma$，根据Hoeffding不等式我们可以得到$P(A_{i}) \leq 2 \exp (-2 \gamma^{2} m)$.因此，可以做出如下推导：
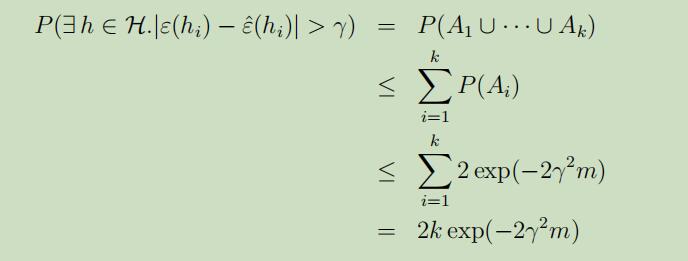如果我们将上式两边都用1减去，我们发现：
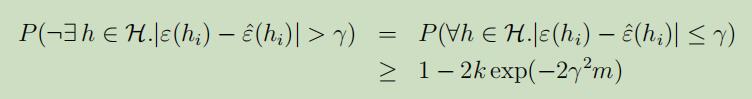对于所有样本$h \in \mathcal{H}$的误差都小于$γ$的概率至少为$1-2 k \exp (-2 \gamma^{2} m)$,这个结果可以被称之为一致收敛，这是因为这是对所有的$h \in \mathcal{H}$都同时拥有了一个下界。
在这上面的讨论中，我们所做的事为，给定特定的值m和γ的情况下，对于一些$h \in \mathcal{H},|\varepsilon(h)-\hat{\varepsilon}(h)|>\gamma$的概率给定一个上界或者下界。在这其中有我们所感兴趣的三个定量：m,γ和错误的概率；我们可以使用其中的两个来限定另一个量的取值。
举个例子来进行解释，首先回答这个问题：当给定γ和$\delta>0$，我们为了保证训练误差和泛化误差之间的差值小于γ，需要m的值为多少？答案为：通过设$\delta=2 k \exp (-2 \gamma^{2} m)$并用此来解出m：
因此就可以徐艳定出我们所需要保证的最少的训练集的数量，为了确保能具有一定等级的效能，算法所需要的训练集的大小m也被称为算法的取样复杂度。
其中最为重要的的一条属性就是，确保概率的情况下，所需要的训练集的数量仅是关于k的对数形式。
相似地，我们也可以固定m和$\delta$来解出γ在之前的等式中，当概率为$1-\delta$时，对于所有的$h \in \mathcal{H}$我们有：
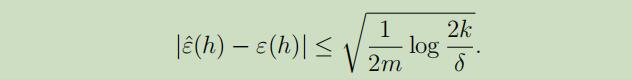
当我们选取$\hat{h}=\arg \min _{h \in \mathcal{H}} \hat{ε}(h)$的时候，我们该如何来证明我们的学习算法的泛化是否是正确的呢？
现在定义$h^{\ast}=\arg \min _{h \in \mathcal{H}} ε(h)$为H中最优的假设，所以我们使用$h^{\ast}$来对性能进行比较是很有意义的。如下：
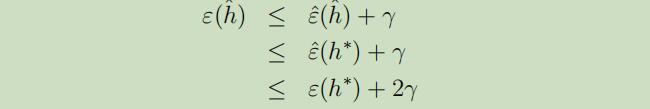
第一行是因为样本一致收敛，即$|\varepsilon(\hat{h})-\hat{\varepsilon}(\hat{h})| \leq \gamma$。
第二行是因为使用$\hat{h}$来最小化$\hat{\varepsilon}(h)$，因此对于所有的h有$\hat{\varepsilon}(\hat{h}) \leq \hat{\varepsilon}(h)$，特别是$\hat{\varepsilon}(\hat{h}) \leq \hat{\varepsilon}(h^{\ast})$。
第三行再次使用了一致收敛，$\hat{\varepsilon}(h^\ast) \leq {\varepsilon}(h^\ast)+\gamma$\
所以我们可以看出来，当均符合一致收敛时，$\hat{h}$的泛化误差最多比$H$中的最优假设糟糕$2γ$。
定理： 令$|\mathcal{H}|=k$，所有的m和δ都固定，使概率最少为$1-δ$，我们可以得到：
这样就可以把我们先前提过的模型选择中的偏差/方差 折中给定量化，特别的，当我们给定一个更大的假设类$\mathcal{H}^{\prime} \supseteq \mathcal{H}$是，上式中的第一项 $\min _{h} \varepsilon(h)$只会变小（这是因为其取最小值，只可能比现在更小），这样的话，通过对的一个更大的假设类进行学习，我们的“偏重”只能减少。另外，当k也在增加的同时，式子中第二部分将会增加，并且这也会导致“方差”增加。（注意，这里把第一项看作为偏差，第二项看作为方差，只是近似的，并不是十分的正规）
接着，我们同样也可以得到如下的取样复杂度界限：
Corollary：令$|\mathcal{H}|=k$，所有$\delta, \gamma$都固定，然后保持$\varepsilon(\hat{h}) \leq \min _{h \in \mathcal{H}} \varepsilon(h)+2 \gamma$的概率最少为$1-δ$，就可以满足：
4.无限H的例子
当假设类H包含了被实数化的无限数量的函数，比如线性分类器，我们可以得到类似于有限H的结论吗？
现在让我们来从下面这个并不是那么正确的讨论开始，帮助我们提高对这一领域的直觉认识。
假设我们有被d个实数参数化的假设类$\mathcal{H}$，在计算机中是使用双精度浮点数来表示实数，因此对于每一个$h \in \mathcal{H}$就需要64位来表示，这样不同假设类最多有$k=2^{64 d}$个不同的假设。从Corollary可知，在保证$\varepsilon(\hat{h}) \leq \varepsilon(h^{\ast})+2 \gamma$的概率最小为$1-δ$时，可以满足
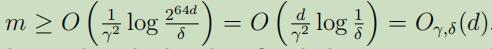（其中，下标$\gamma, \delta$和表示依赖于隐藏的常量$\gamma$和$\delta$）
这个例子可以让我们看出来，所需要的训练样本的数量和模型的参数是线性关系
可以得出结论，虽然在现实中假设类依赖于64位的浮点数并不能完全的满足，但是我们得出的结论差不多是正确的：如果我们想要去最小化训练误差，然后为了学习能有好的质量而使用具有d个参数的假设类，通常我们所需要的训练样本数就是d的线性关系。 （值得注意的是，取样复杂度m的这种线性关系在大多数ERM方法中都符合，但是给与那些非ERM学习算法很好的理论保证仍然是很好的）
上述的假设还有点不太满足的地方在于对于$\mathcal{H}$的参数化，但这看起来并不是一个很大的问题：我们曾经把我们的线性分类器定义为$h_θ(x)=1\lbrace θ_{0}+θ_{1} x_{1}+…+ \theta_{n} x_{n} \geq 0\rbrace$，其中有n+1个参数$\theta_{0}, \ldots, \theta_{n}$。但是我们同样也可以把线性分类器写成如下的形式$h_{u, v}(x)=1\lbrace (u_{0}^{2}-v_{0}^{2})+(u_{1}^{2}-v_{1}^{2}) x_{1}+…+(u_{n}^{2}-v_{n}^{2}) x_{n} \geq 0\rbrace$，这是就有2n+2个参数$u_{i}, v_{i}$。然而这些仅是定义了相同的$\mathcal{H}$：n维线性分类器的集合。
为了能够导出更有说服力的论点，我们定义如下符号： 给定点$x^{(i)} \in \mathcal{X}$的数据集$S=\lbrace x^{(i)}, …, x^{(d)}\rbrace$，如果$\mathcal{H}$能够实现对集合$S$的任意标记，那么我们可以称之为$\mathcal{H}$Shatters$S$。例如：对于任意的标签集$\lbrace y^{(1)}, …, y^{(d)}\rbrace$存在一些$h \in \mathcal{H}$对于所有的$i=1, \ldots d$能够有$h(x^{(i)})=y^{(i)}$。
对于一个给定的假设类$\mathcal{H}$，我们定义它的Vapnik-Chervonenkis 维度为$\mathcal{H}$最大可以shatter的结合的大小，记为$\mathrm{VC}(\mathcal{H})$。
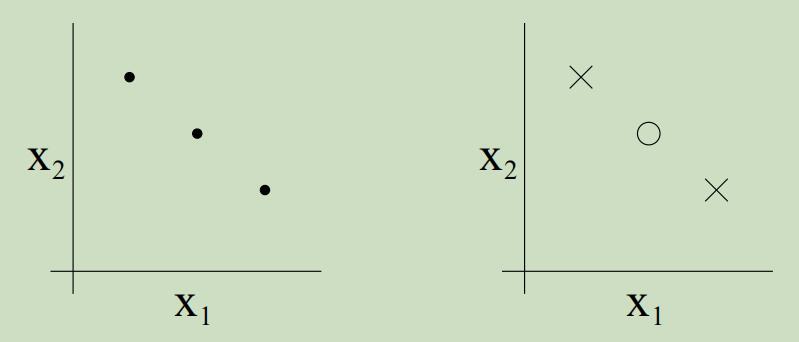
例如，考虑如下三个点的集合：
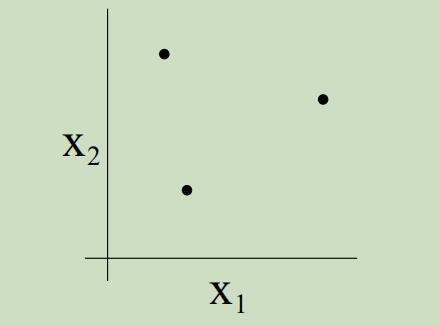二维的线性分类器集合可以shatter上面的集合吗？yes。我们可以看到，对于这三个点所有可能的标签，我们都可以找到一条“0误差”的线来划分它们
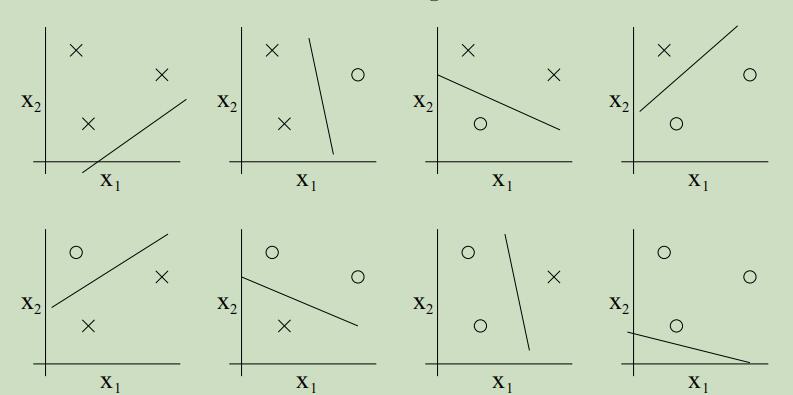但是对于4个点的集合，假设类H就一定不能对其进行shatter。因此，H可以chatter的最大大小为3，故$\mathrm{VC}(\mathcal{H})=3$。
需要注意的是，只有对于d大小的集合来说，至少要能有一种集合$\mathcal{H}$可以shatter的。例如下图，虽然不能shatter，但是$\mathrm{VC}(\mathcal{H})=3$。
根据VC,下面可以来介绍下一个定理了，这个定理可以说是学习原理汇总最为重要的定理了。
定理：给定$\mathcal{H}$，$d=\mathrm{VC}(\mathcal{H})$。在确保$|\varepsilon(h)-\hat{\varepsilon}(h)| \leq 2γ$的概率最小为$1-δ$时，对于所有的$h \in \mathcal{H}$有
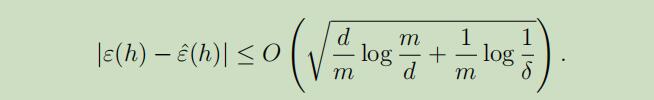同样也可以得出
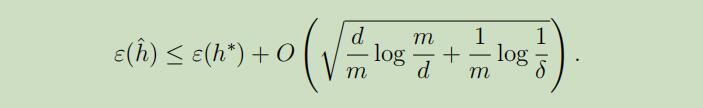
换句话说，如果假设类有有限的VC维度，那么当m很大的时候就会一致收敛，如同之前一样，这将允许我们根据$\varepsilon(h^{\ast})$给$\varepsilon(h)$一个界限。我们可以获得如下的Corollary： Corollary： 对于所有的$h \in \mathcal{H}$使$|\varepsilon(h)-\hat{\varepsilon}(h)| \leq 2γ$的概率最小为$1-δ$，这将满足$m=O_{\gamma, \delta}(d)$。
从这上面讲述的内容中，我们可以总结出，对于绝大多数假设类，VC维度同样粗略的和参数的个数线性相关，因此所需的训练样本的数量也粗略的和$\mathcal{H}$的参数个数线性相关。
