网易公开课视频地址：http://open.163.com/movie/2008/1/O/T/M6SGF6VB4_M6SGKGMOT.html 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes7a.pdf， https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes7b.pdf， https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes8.pdf
Lecture 12 - k-means，Mixtures of Gaussians，EM algorithm
K-means
给定一组没有标签的数据集$\lbrace x^{(1)}, \ldots, x^{(m)}\rbrace$，想要把数据划分为几个相互紧密连接的聚类。 K-means算法流程如下：
- 随机初始化聚类中心$\mu_{1}, \mu_{2}, \dots, \mu_{k} \in \mathbb{R}^{n}$
- 重复直到收敛：
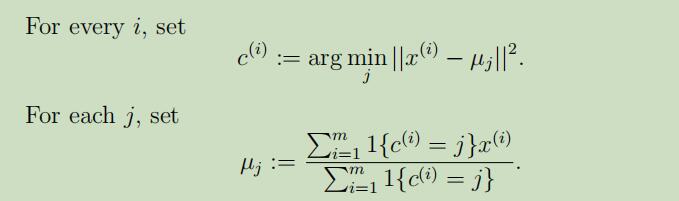
在上面的算法中，参数k是我们所需要划分的聚类的数量，聚类中心$\mu_{j}$表示我们对聚类中心位置的猜测坐标。在最开始初始化聚类中心的时候，我们可以选择k个随机的训练样本来当做训练中心，并且这些聚类中心的值就位其相对应样本的值。（或者其他的选择方法也皆可以）。
算法的内存循环主要包括两步：（1）为每个训练样本$x^{(i)}$分配一个离其最近的聚类中心$\mu_{j}$。（2）对所属聚类中心$\mu_{j}$的样本取平均值，并用这个平均值来更新$\mu_{j}$。
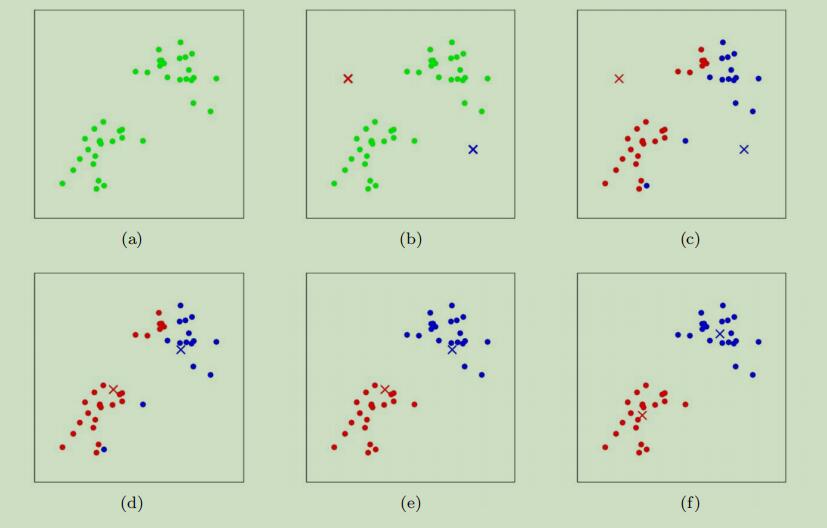
如下图1，生动的展示了K-means算法得运行过程。
K-means算法一定能保证收敛吗？ 是的。现在让我们定义失真函数（distortion function）如下：
函数J测量的是每个样本点距离其分配的聚类中心的距离总和，k-means可以被视为J上的坐标下降。更明确些，k-means的内层循环重复地在保持$\mu$不变的情况下使用$c$对函数J最小化，在保持$c$不变的情况下使用$\mu$对函数J最小化，因此J一定是单调递减，所以J的值一定会收敛（这也通常意味着，$\mu$和$c$的值最后也会收敛）。从原理上来说，k-means有可能在不同的聚类之间来回摇摆，例如对于不同的$c$,$\mu$有相同的J，但这种情况在实际中很少发生。
还有一点要注意，失真函数J是非凸函数，所以J上的坐标下降并不能保证收敛到全局最小值。尽管如此，k-means通常都能划分出很好的聚类，但是如果你非常担心陷入到了一个很糟糕的局部最小值中，可以使用不同的聚类中心来初始化，并挑选具有最小失真函数$J(c, \mu)$的那个结果。
混合高斯模型（mixture of Gaussians）
再讲混合高斯模型和EM算法之前，需要先介绍一下密度估计问题。
给定一组飞机零件，我们获得了这些零件的震动频率和发热量两个属性，并将其绘制如图，假设现新增了一个零件如图中点所示，那么是不是有错误的零件呢？
现在如果我们为图中特征的典型概率分布建立成$P(x)$的模型，当新的零件的$P(x)$特别小时，我们就认为这是一个异常的产品， 因为同种的样本点并不是我们所知道的典型概率分布，所以我们怎么能为这些样本点建立相应的概率分布呢？
再举一个例子，如图上方是一维数据展开为二维高斯分布的例子，下方则更明确了些，给出了每个点所具有的类别，并对每个类别的点绘制出其相对应的高斯分布，最终的概率分布就是两个高斯分布之和。
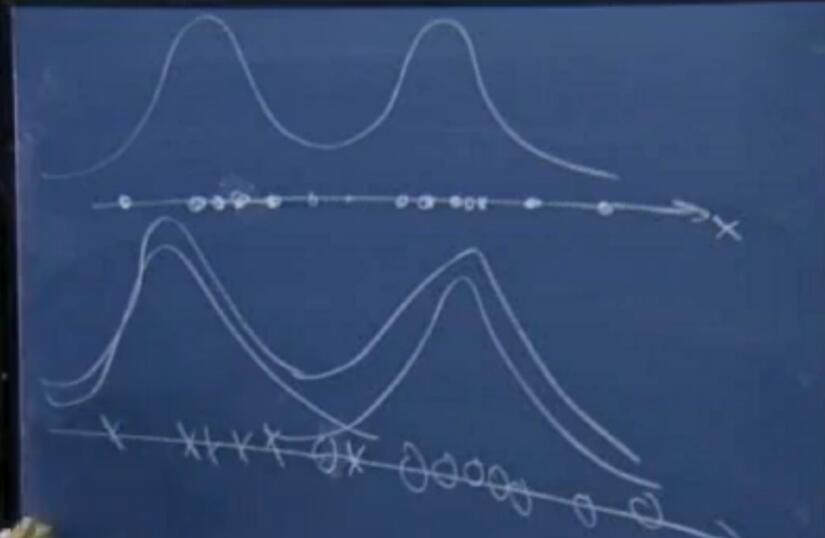但现在问题就是，不知道数据的标签，所以我们要做的就是用一个算法来拟合出这两个混合在一起的高斯分布。
设$z^{(i)}$为潜在（latent）随机变量，即隐藏起来的看不见的变量。
假设给定一组无标签数据集$\lbrace x^{(1)}, \ldots, x^{(m)}\rbrace$，我们希望来通过明确一个联合分布$p(x^{(i)}, z^{(i)})=p(x^{(i)} | z^{(i)}) p(z^{(i)})$来对数据建模。这里$z^{(i)} \sim$ Multinomial $(\phi)$（其中$\phi_{j} \geq 0$，$\sum_{j=1}^{k} \phi_{j}=1$，参数$\phi_{j}$表示$p(z^{(i)}=j)$），还有$x^{(i)} | z^{(i)}=j \sim \mathcal{N}(\mu_{j}, \Sigma_{j})$。
令k表示$z^{(i)}$所能包含的数值的个数，因此我们的模型假设： 每一个$x^{(i)}$是通过随机从$\lbrace 1, \ldots, k\rbrace$中选择$z^{(i)}$来产生的，并且$x^{(i)}$从依赖于$z^{(i)}$的k个高斯分布其中的一个导出的。这样的模型称之为混合高斯模型。但潜在随机变量的存在使得我们的估计问题变得困难。
为了估计我们模型中的参数$\phi, \mu$ 和 $\Sigma$，我们可以写出数据的似然函数如下：
然而，如果我们把这个公式的导数设为0并尝试去求解，我们会发现不可能去找到这些参数的极大似然估计值。
随即变量$z^{(i)}$表示出了每个$x^{(i)}$是来自于k个高斯分布中的哪一个，假如现在我们知道了$z^{(i)}$具体的值，那么极大似然问题将会变得很简单。我们可以写出如下形式的似然函数：
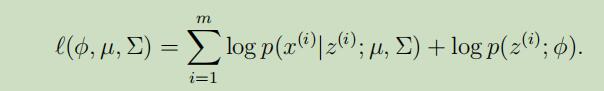并获得$\phi, \mu$ and $\Sigma$的极大似然估计值如下：
事实上，当我们知道了$z^{(i)}$后，参数的估计就和以前学过的高斯判别分析模型中的参数估计大致一样
EM(Expectation-Maximization) algorithm
然而，在我们的密度估计问题中，$z^{(i)}$的值是不知道的，那我们该怎么办呢？
来看看下面的EM算法。EM算法是一个具有两步的迭代算法，现在我们将其应用到我们的问题中来。
在E-step中，它尝试去“猜测”$z^{(i)}$的值，在M-step中，它基于我们的猜测来更新模型中的参数 （这里假设了第一步中的猜测是正确的）。
算法如下：
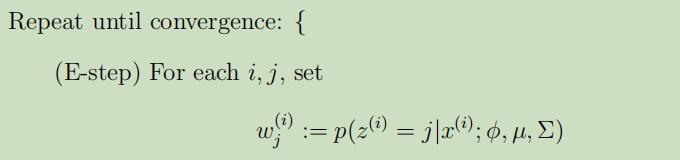
$w_{j}^{(i)}$是对$z^{(i)}$值的一种“软猜测”
在E-step中，我们计算了$z^{(i)}$的后验概率，对其使用贝叶斯公式我们可以得到：
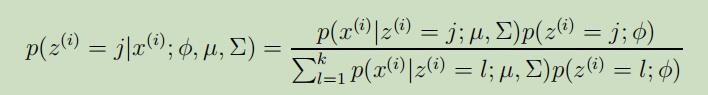这里$p(x^{(i)} | z^{(i)}=j ; \mu, \Sigma)$由均值为$\mu_{j}$和协方差为$\Sigma_{j}$的高斯分布给出；$p(z^{(i)}=j ; \phi)$由$\phi_{j}$给出。
在M-step的参数更新中，除了指示函数1$\lbrace z^{(i)}=j \rbrace$被替换为$w_{j}^{(i)}$外，其他的都与$w_{j}^{(i)}$已知时的参数更新一致。
这个EM算法同样可以让我们回忆起k-means聚类算法，不过这里我们没有像k-means一样使用“硬”聚类分配$c(i)$策略，而是使用了“软”分配$w_{j}^{(i)}$。它和k-means算法一样，容易得到局部最优解，所以我们最好也多次重复初始化参数来得到更好的解。
EM算法原理详细解释
我们可以很清楚的从EM算法中看出来他重复地尝试去猜测$z^{(i)}$的值，但是$z^{(i)}$是怎么得到的？我们怎样才能确保算法一定收敛呢？在这一章节，我们将会介绍EM算法更广阔的的视角，并展示它是怎么样应用到具有潜在变量的估计问题中去。
Jensen’s 不等式
令$f$为实凹函数（$f^{\prime \prime}(x) \geq 0$），在$f$采取向量为输入时，可以推广到他的hessian矩阵$H$时半正定矩阵。当$f^{\prime \prime}(x)>0$时，f是严格凹函数，再采取向量为输入的情况下它的hessian矩阵H一定是正定矩阵。
定理： 令$f$为凹函数，并且令$X$为随机变量，将会有
当$f$是严格凹函数时，当且仅当$X=\mathrm{E}[X]$时有
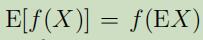
为了能更好的解释这个定理，看下图：
X是一个随机变量，它取值为a的概率为0.5，取值为b的概率为0.5。X的期望EX就是a和b在x轴上的中点。E(f(x))就是f(a)和f(b)在y轴上的中点
Remark： 当且仅当$-f$为[严格]凹函数时，$f$是[严格]凸函数（$f^{\prime \prime}(x) \leq 0$ or $H \leq 0$）。当$f$为凸函数时，Jensen’s 不等式仍然成立，不过结果变成了$\mathrm{E}[f(X)] \leq f(\mathrm{E} X)$
EM算法原理
假设我们的估计问题由m个独立的训练样本$\lbrace x^{(1)}, \ldots, x^{(m)}\rbrace$组成，我们需要对这些数据拟合模型$p(x, z)$的参数，模型的似然函数如下：
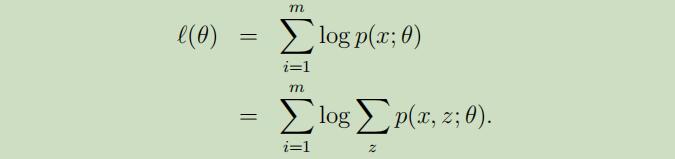
但是，因为潜在随机变量$z^{(i)}$的存在，使对上式子来寻找参数θ的极大似然估计可能非常的困难。然而，如果当明确了$z^{(i)}$时，对上式子进行极大似然估计将会是很容易的。
在这种设定下，EM算法为我们提供了一种有效的方法来进行极大似然估计。明确的最大化$\ell(\theta)$可能比较困难，所以我们的方法是重复地去对$\ell(\theta)$构建一个更低的约束（E-Step）,并对这个更低的约束进行优化（M-step）
现在对于每个i，令$Q_{i}$为$z^{s}$上的一些分布（$\sum_{z} Q_{i}(z)=1$，且$Q_{i}(z) \geq 0$）。现在再来考虑上面的似然函数：
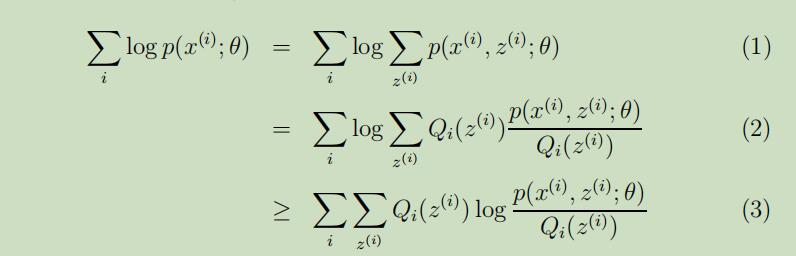
第三步的推导过程使用了Jensen不等式，具体推导过程如下：
$f(x)=\log x$，且$f^{\prime \prime}(x)=-1 / x^{2}<0$，所以$f(x)$是一个凸函数。
上面这个累加公式可以看作为$[p(x^{(i)}, z^{(i)} ; \theta) / Q_{i}(z^{(i)})]$的期望，并且这个期望在公式（2）中是凸函数$\log$的参数，因此根据Jensen不等式可以得到：
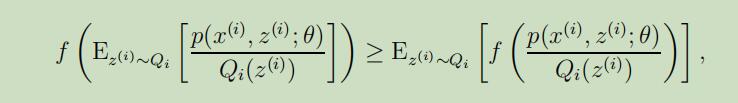
所以现在，我们对公式（3）有了更低的约束。但请思考另一个问题：我们应该怎么来选择$Q_{i}^{\prime} s$呢？ 答案如下：当我们有一些参数的当前猜测θ，很自然的可以尝试去使这个约束在参数θ的值上变得严格符合；例如，我们可以使用特定的θ值来使不等式变为等式。
所以我们现在所需要做的就是讲涉及Jensen不等式那步的不等式变为等式。正如我们所知，期望可以采用“常量”作为随机变量，这样就符合了Jensen等式的条件。故可令：
而这个“常量化”过程可以通过选择如下$Q_{i}$来实现：
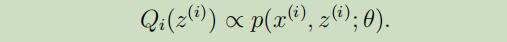
实际上，我们还有个关于$Q_{i}$的条件可以使用，$\sum_{z} Q_{i}(z^{(i)})=1$，这可以帮我们进一步明确$Q_{i}$的选择：
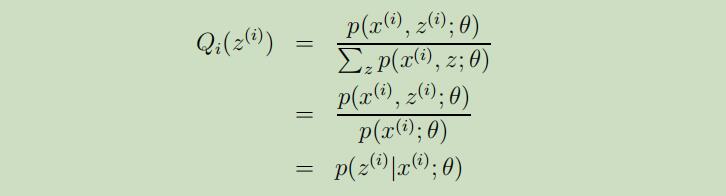
现在，在我们有了明确的$Q_{i}$后，我们可以得到现在的EM算法如下：
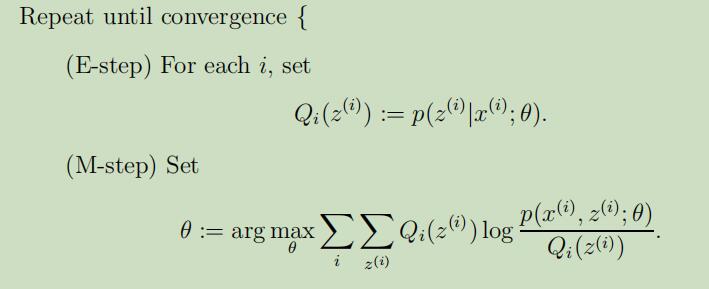
但是我们该怎么判断算法收敛了呢？现在来让我们假设在EM算法中连续的两轮迭代中获得了$\theta^{(t)}$和$\theta^{(t+1)}$两个参数，若我们能证明出$\ell(\theta^{(t)}) \leq \ell(\theta^{(t+1)})$，则同样可以证明出EM算法中的对数似然函数是单调递增的。
在选择$Q_{i}^{(t)}(z^{(i)}) :=p(z^{(i)} | x^{(i)} ; \theta^{(t)})$保证了Jensen等式的条件下，我们可以得到：
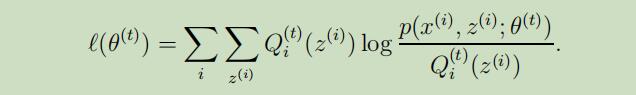
因为参数$\theta^{(t+1)}$是通过最大化$\ell(\theta^{(t)})$得到的参数，故：
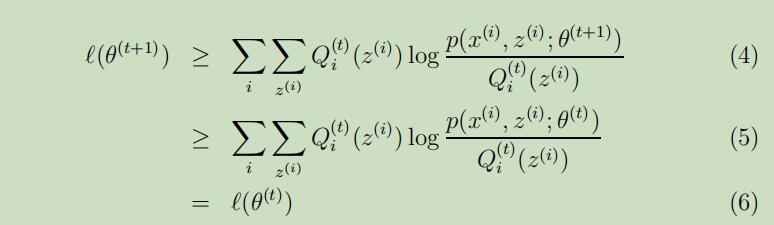
第（4）步由公式（3）得到
因此，EM就使得似然函数单调递增直到收敛。一种合理的收敛测试方法为检测两次连续的迭代间$\ell(\theta)$的增长是否小于特定的容忍参数。
Remark：如果我们定义
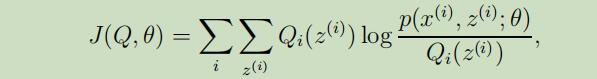
在我们先前的推导过程中，已知$\ell(\theta) \geq J(Q, \theta)$。EM算法同样可以看作为J上的坐标上升，在E-step中根据Q最大化，在M-step中根据θ最大化。
EM算法参数更新过程推导
在E-step中，我们可以很轻松的得到如下：
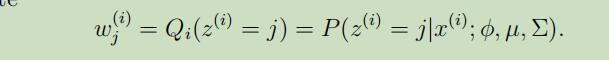
在M-step中，我们需要对如下公式最大化，来得到我们的参数$\phi, \mu, \Sigma$
对上式对$\mu_{l}$求偏导，得到：
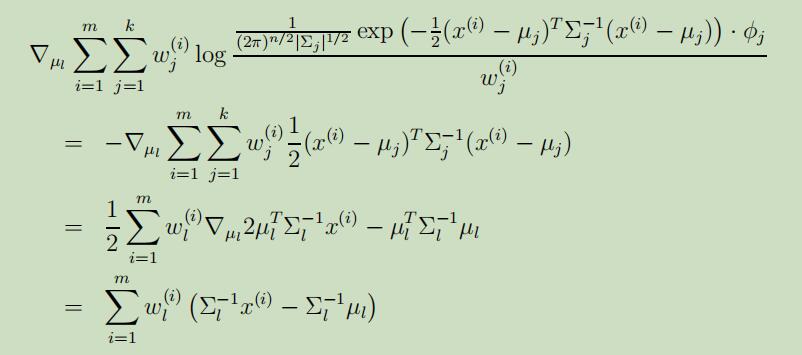将其设为0后，并求解出$\mu_{l}$，来得到$\mu_{l}$的更新公式：
对于参数$\phi_{j}$，我们所需要最大化的公式可以简化为：
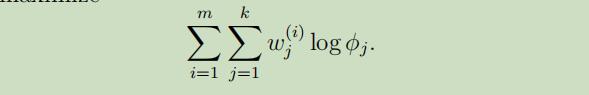但是，关于$\phi_{j}$我们有个条件约束，$\sum_{j=1}^{k} \phi_{j}=1$，故我们可以构建了格朗日公式：
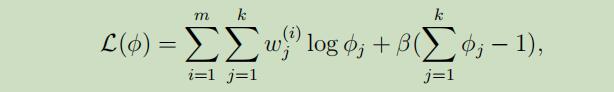其中 $\beta$为拉格朗日乘数。对上式求偏导，我们可以得到
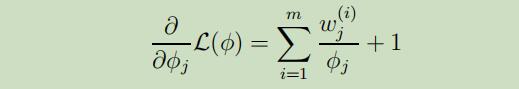
将其设为0并求解，可以得到：
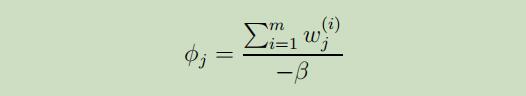
根据条件$\sum_{j} \phi_{j}=1$我们可以得到$-\beta=\sum_{i=1}^{m} \sum_{j=1}^{k} w_{j}^{(i)}=\sum_{i=1}^{m} 1=m$。因此我们可以得到参数$\phi_{j}$的更新规则：
$\Sigma_{j}$的推导过程见作业。
