视频地址：https://www.bilibili.com/video/av49432977/?p=14 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes10.pdf
Lecture 14 - 主成成分分析(Principal components analysis)
在本部分内容我们将介绍一种PCA方法，同样可以识别出数据所约在的子空间，但是其更为直接，只需要一个特征向量的计算，且不需要求助于EM。
给定以下数据集： ${x^{(i)} ; i=1, \ldots, m}$为m个不同类型汽车的属性，比如说最大速度、转向角等。 $x^{(i)} \in \mathbb{R}^{n}$$(n \ll m)$。但是，假如说有两个属性–$x_{i}$和$x_j$–分别为米每时和千米每时，这样这两个属性就具有了一定的线性依赖，所知这些数据其实是分布在n-1维的子空间中。所以我们该如何去除这些冗余呢？
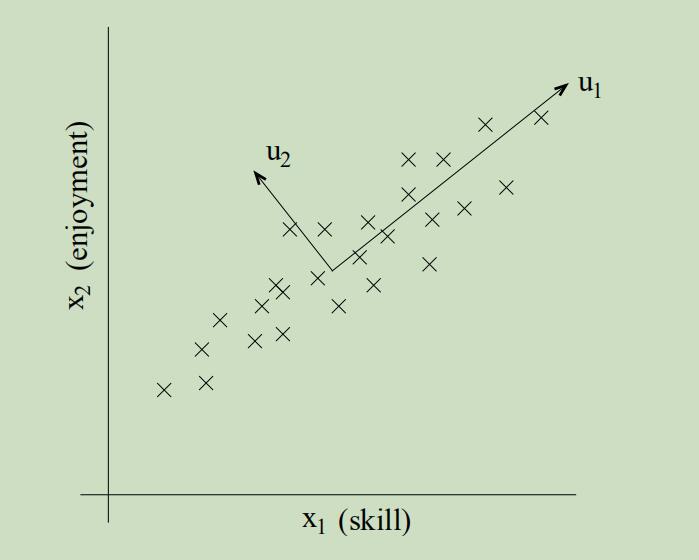
给定另一组更具体的例子，设$x_{1}^{(i)}$为飞行员i的驾驶能力，$x_{2}^{(i)}$是他对飞行的喜爱程度，已知这两个属性具有很强的相关性（只有真正喜欢飞行的才能拥有更高超的飞行能力）。现在将一些样本分别以x1和x2位坐标轴绘制在图上，沿着u1方向能更好的捕捉一个人的驾驶能力，u2方向则为一些噪声，那么我们如何来自动捕捉出u1方向呢？
在PCA算法中，需要先对数据进行预处理步骤，即规范化其均值和方差：
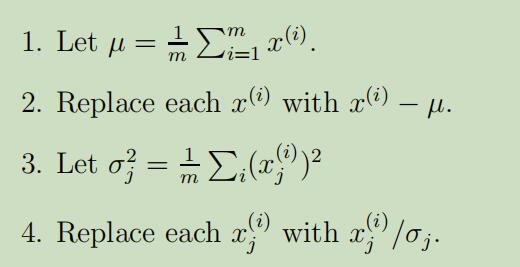其中，(1-2)步的作用为 使数据的均值变为0，(3-4)步的作用为 单位化方差，使不同类型的属性能够在同一个规模上度量。当我们已知所有数据的属性都在相同的规模上时，步骤(3-4)可以省略，例如灰度图中的每一个点$x_{j}^{(i)}$均在${0,1, \ldots, 255}$范围内取值，来表示对于图像i中第j个像素点的密度值。
规范化之后，如何计算出数据所在的主轴u呢？ 一种方法是寻找一个单位向量u，使得样本点在其上投影所得的方差最大化，这样的投影是十分具有信息量的。
已经规范化的数据集样本点如下：
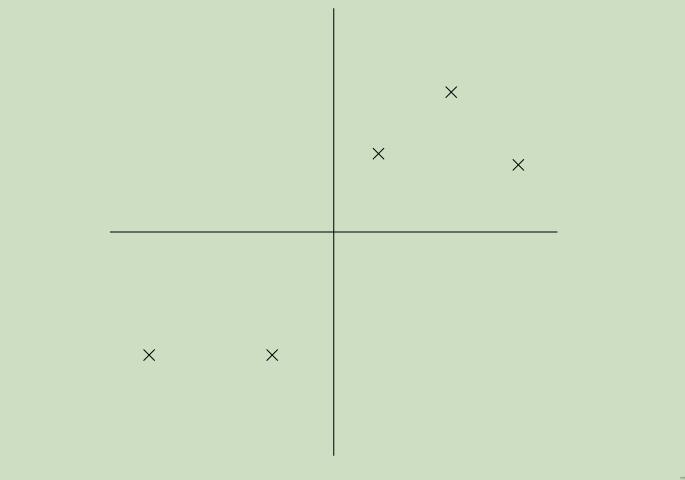
现在令图中的实线为我们所选取的方向u，实心点为样本点在u上的投影。如下图所示，
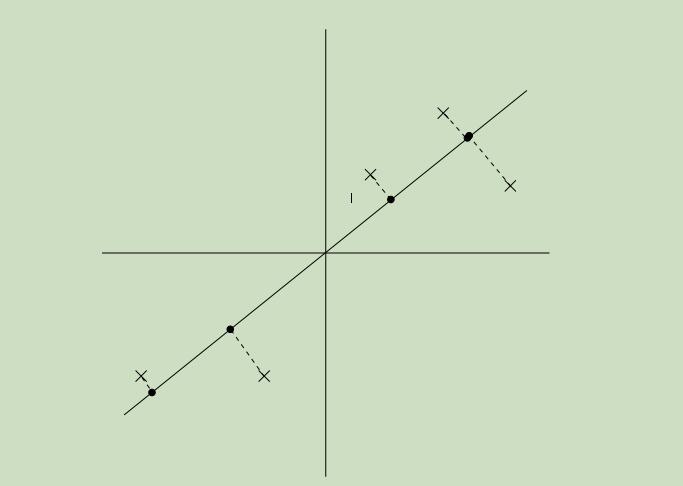
我们可以从图中看出来，投影点距离原点的距离很远，且在方向u上的分布具有很大的方差
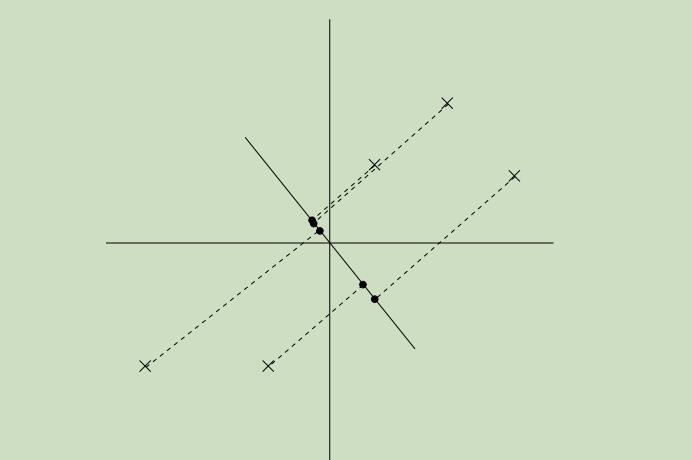
这幅图里，投影在方向u上的方差更小了，并且更接近于原点
因此，我们愿意去自动化选取第一幅图中哪个具有较大方差的方向u。当给定单位向量u和点x时，x在u上的投影长度为$x^{T} u$(也就是投影点到原点的长度)，因此，为了最大化投影的方差，我们需要选择一个单位长度的向量u来最大化：
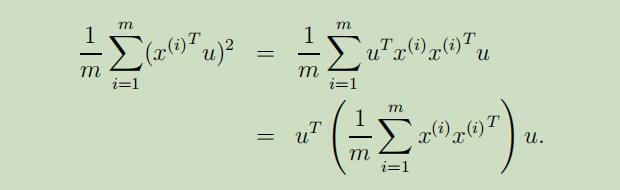
我们可以轻松的辨别出最大化上面的等式可以得到，u就是协方差矩阵$\Sigma=\frac{1}{m} \sum_{i=1}^{m} x^{(i)} x^{(i)^{T}}$的主特征向量。
知识点补充：主特征向量为最大的那个特征值所对应的特征向量。 推导如下：原式子即为条件最值问题
建立的拉格朗日乘数公式为： $L(u,λ)=u^T\Sigma u-λ(u^Tu-1)$ 得到，$\nabla_{u}L = \Sigma u-λu = 0$
总结一下，如果我们想要去寻找数据所在的1维子空间，我们选择u为$\Sigma $的主特征向量；扩展开来，如果我们想要投影我们的数据到k维子空间中$(k<n)$，我们需要选择$u_{1}, \dots, u_{k}$来成为$\Sigma$的k个特征向量。所以这些$u_{i}$就成了新的数据的正交基。
然后，为了展示在这些基础上的$x^{(i)}$，我们仅需要计算如下向量：
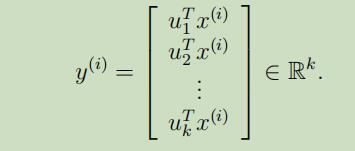
从上可以看出来，虽然$x^{(i)} \in \mathbb{R}^{n}$，但是$y^{(i)}$给了更小维度的$x^{(i)}$的估计，因此，PCA也被称为维度降低算法。向量$u_{1}, \dots, u_{k}$同时也被称作为数据的第k个主成成分。
Remark： 在上面的建模过程中，我们使用的是k=1情况下的例子，使用特征向量的属性我们可以很简单的推广到所有可能的正交基$u_{1}, \dots, u_{k}$，这是只需要最大化$\sum_{i}|y^{(i)}|_{2}^{2}$。因此在我们对基的选择过程中尽可能的保留了原始数据的可变性。
在problem set4，中会有PCA的其他导出方法
PCA的应用
- 压缩
- 可视化
- 降维
- 面部识别
压缩： 使用更低维度的$y^{(i)}$来表示$x^{(i)}$。 可视化： 当把高维度的数据降低到k=2或者k=2维时，我们可以将$y^{(i)}$绘制出来，来观察每一聚类的相似程度。 降维： 预处理学习算法索要使用的数据集，这样可以降低计算难度，还可以降低假设类的复杂程度和避免过拟合。 面部识别： 在一副图片中，$x^{(i)} \in \mathbb{R}^{100 \times 100}$，为10000维的向量，使用PCA我们可以替换为更低纬度的$y^{(i)}$。在这样做的过程中，我们希望我们发现的主要组件保留了一个人真正看起来像的脸之间的有趣的、有系统的变化，而不是图像中的“噪声”引入轻微的照明变化，略有不同的成像条件，等等。然后我们在低纬度空间中，通过计算$|y^{(i)}-y^{(j)}|_{2}$来计算不同面部i和j之间的变化。这可以得到一个效果好的面部识别算法。
SVD（奇异值分解）
以下内容部分借鉴自https://blog.csdn.net/xiaocong1990/article/details/54909126, https://www.cnblogs.com/pinard/p/6251584.html
相比于特征分解，奇异值分解可以使用于任意的矩阵，例如可以将矩阵A分解如下：
$A=U \Sigma V^{T}$
其中A是$m \times n$维的矩阵,U是$m\times m$的方阵（每一向量均正交，且称之为左奇异向量），$\Sigma $是一个$m\times n$维的对角矩阵（对角线上的元素称为奇异值），V是一个$n \times n$维的矩阵（同样向量两两正交，且称之为右奇异向量）
形象化展示如下图：
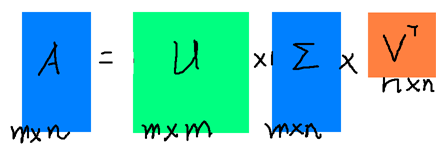
那么奇异值和奇异向量从何而来呢？
如果我们将A的转置和A做矩阵乘法，那么会得到$n \times n$的一个方阵$A^TA$。既然$A^TA$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：
$\left(A^{T} A\right) v_{i}=\lambda_{i} v_{i}$
将$A^TA$的所有特征向量张成一个$n \times n$的矩阵V，就是我们SVD公式里面的V矩阵了,也就是A的右奇异向量。
同样，对$m \times m$的方阵$AA^T$，进行特征分解可以得到：
$\left(A A^{T}\right) u_{i}=\lambda_{i} u_{i}$
将$AA^T$的所有特征向量张成一个$m \times m$的矩阵U，就是我们SVD公式里面的U矩阵了。也就是A的左奇异向量。
关于奇异值$\sigma$， 可以有以下推导得出：
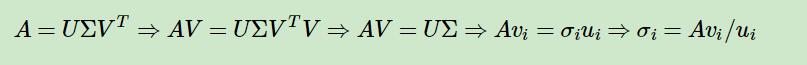另外，还有一种方式，$A^TA$的特征值与奇异值满足如下关系：
$\sigma_{i}=\sqrt{\lambda_{i}}$
SVD的性质
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。 也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$A_{m \times n} \approx U_{m \times r} \Sigma_{r \times r} V_{r \times n}^{T}$
r是一个远小于m、n的数,这样矩阵A可以用三个更小的矩阵来表示了。
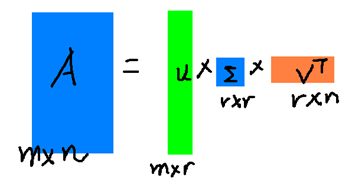
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，在这儿，r越接近于n，则相乘的结果越接近于A。
SVD与PCA之间的关系
这里再补充一个小知识：PCA中的协方差矩阵可以表示为$X^TX$
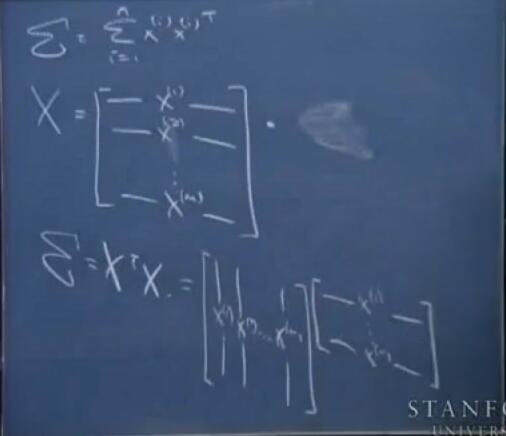
在主成分分析（PCA）中，我们讲到要用PCA降维，需要找到样本协方差矩阵$X^TX$的最大的d个特征值对应的特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$X^TX$，当样本数多样本特征数也多的时候，这个计算量是很大的。 因此，我们对$X$使用SVD算法，所得到的右奇异向量即为我们所需要的特征向量, 并且这并不要求我们先求出协方差矩阵$X^TX$。
另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？
假设我们的样本是$m \times n$的矩阵X，如果我们通过SVD找到了矩阵$XX^T$最大的d个特征向量张成的$m \times d$维矩阵U，则我们如果进行如下处理：
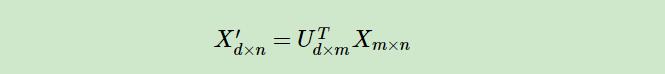
可以得到一个$d \times n$的矩阵X‘,这个矩阵和我们原来的$m \times n$维样本矩阵X相比，行数从m减到了d，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。
LSI(潜在语义索引)
部分摘抄自https://blog.csdn.net/appleyuchi/article/details/85225509，https://blog.csdn.net/xiaocong1990/article/details/54909126/
在对文本进行处理时，给出如下的矩阵：
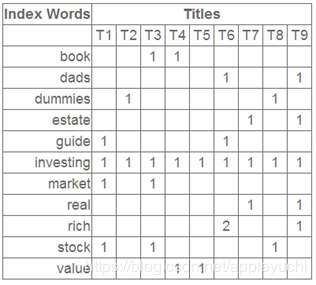在应用SVD之后得到：
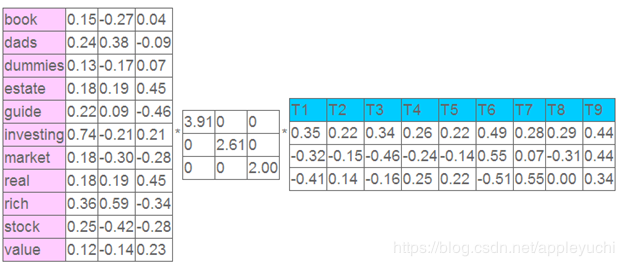
左奇异向量表示词的一些特性，右奇异向量表示文档的一些特性，中间的奇异值矩阵表示左奇异向量的一行与右奇异向量的一列的重要程度，数字越大越重要。
继续看这个矩阵还可以发现一些有意思的东西，首先，左奇异向量的第一列表示每一个词的出现频繁程度，虽然不是线性的，但是可以认为是一个大概的描述，比如book是0.15对应文档中出现的2次，investing是0.74对应了文档中出现了9次，rich是0.36对应文档中出现了3次；
其次，右奇异向量中一的第一行表示每一篇文档中的出现词的个数的近似，比如说，T6是0.49，出现了5个词，T2是0.22，出现了2个
在上面的图片中，T1和T3（我们从上往下看），各自都是一列，看作为各自的向量，利用这个两个向量之间的余弦相似度即可衡量两个文档T1和T3的不同。
