视频地址：https://www.bilibili.com/video/av49432977/?p=15 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes11.pdf
Lecture 15 - Independent Components Analysis（独立成分分析）
鸡尾酒宴会问题
考虑如下鸡尾酒宴会问题：n个发言者同时在宴会上讲话，并且n个不同的麦克风被放置在房间里来录制多个发言人重叠的讲话，因为这些麦克风距离每个人的距离都不一样，所以它们记录的不同发言人的声音大小也不一样，离的近的声音大，离得远的声音小。使用这些录制的音频，能否将这些发言人的声音信号分离开呢？
为了形式化展示上述问题，我们设n个发言人独立的讲话为$s \in \mathbb{R}^{n}$，而我们所观察到的则为
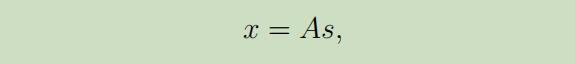其中A是未知的方阵，称作为混合矩阵（mixing matrix） 。在进行了多次观测之后，我们得到数据集$\lbrace x^{(i)} ; i=1, \dots, m\rbrace$，并且我们的目标为从生成的数据（$x^{(i)}=A s^{(i)}$）中，恢复我们的原数据$s^{(i)}$
现在令$W=A^{-1}$为逆混合矩阵 ，我们的目标则为寻找到一个$W$，可以通过计算$s^{(i)}=W x^{(i)}$来恢复我们的数据源。为了便携起见，我们令$w_{i}^{T}$表示$W$的第i行，所以
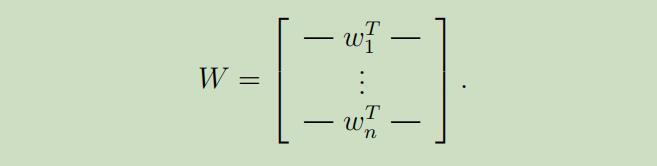
因此，$w_{i} \in \mathbb{R}^{n}$,并且数据源的计算方式 变为$s_{j}^{(i)}=w_{j}^{T} x^{(i)}$，其中$s_j^{(i)}$为在第i个时间第j个人说的内容。
ICA不确定性（ICA ambiguities）
在对A和s没有任何先验知识的情况下，很难仅根据X，去恢复出确定的s。
第一种情况： 假设A为任意的n阶置换矩阵
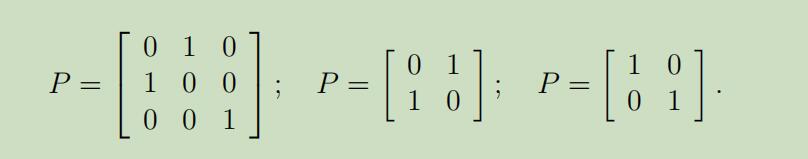给定一个s向量，那么$As$只是s向量中坐标的置换，如果我们通过改变s中坐标和A中列向量的顺序，那么将得到同一个X，从而无法唯一确定s。
辛运的是，这对大多数应用来说影响不大。
第二种情况： 将A替换为2A，每个$s^{(i)}$都替换为$(0.5) s^{(i)}$，那么我们可以观察到$x^{(i)}=2 A \cdot(0.5) s^{(i)}$得到的仍然是相同的$x^{(i)}$。若将0.5替换为其他的数，那么数据源s的规模大小也就无法确定了。
但是，这对我们的鸡尾酒宴会问题来说，这并不是一个问题，因为s的系数只会改变发言人声音的大小。我们可以控制这个系数来恢复正常的音量大小。
第三种情况： 当数据源服从标准高斯分布时，$s \sim \mathcal{N}(0, I)$，其密度函数的图像是圆心为零点的圆，并且图像是沿着任何一个轴螺旋对称的，因此在即使拥有无穷大的数据集时，仍然找不到数据所倾向的那个方向。
这种情况的另一种解释为：当给定$x=A s$时，$x \sim \mathcal{N}(0,AA^T)$($\mathrm{E}[x x^{T}]=\mathrm{E}[A s s^{T} A^{T}]=A A^{T}$)。现在给定正交矩阵R，令$A^{\prime}=A R$且$x^{\prime}=A^{\prime} s$，这时得到$x^{\prime}$是和$x$一样的高斯分布，$\mathrm{E}[x^{\prime}(x^{\prime})^{T}]=\mathrm{E}[A^{\prime} s s^{T}(A^{\prime})^{T}]=\mathrm{E}[A R s s^{T}(A R)^{T}]=A R R^{T} A^{T}=A A^{T}$。 因此，将无法分辨出数据源是被A还是$A^{\prime}$混合，无法恢复出源数据。
密度函数和线性变换（Densities and linear transformations）
当已知密度函数$p_{s}(s)$时，如何根据$x=As$推断出x的密度函数$p_x$?
这里需要对我们的概率论知识进行一个回顾。
设$s \sim U[0,1]$，密度为$p_{s}(s)=1\lbrace 0 \leq s \leq 1\rbrace$，推断如图所示：
所以总结的转换规则如下：
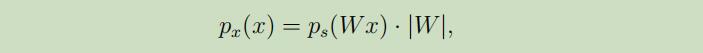
其概率论的推导过程如下：
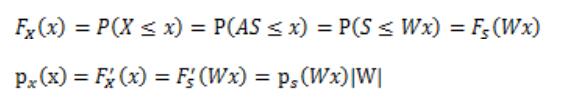
ICA 算法
在每个源$s_{i}$的密度函数为$p_s$，且每个$s_i$相互独立的情况下，源s的联合分布为：
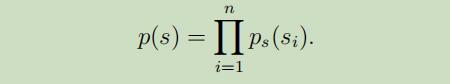
在使用我们导出的公式，来讲s的密度函数替换为x的密度函数，得到：
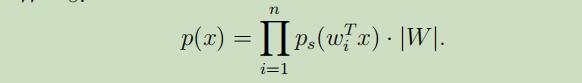
为了明确每个源s的密度函数，我们需要用到分布函数（CDF），已知$p_{z}(z)=F^{\prime}(z)$。
所以，目前我们所需要的仅为找到一个合适的分布函数，对其求导即可得到s的密度函数。在除了高斯分布之外，我们需要找到一个函数是从0到1的单增函数，且其导函数的均值为0 ，一般而言我们可以将其选择为sigmod函数 ，即$p_{s}(s)=g^{\prime}(s)$
方阵W使我们模型中的参数，在给定训练集$\lbrace x^{(i)} ; i=1, \ldots, m\rbrace$时，其对数似然函数为
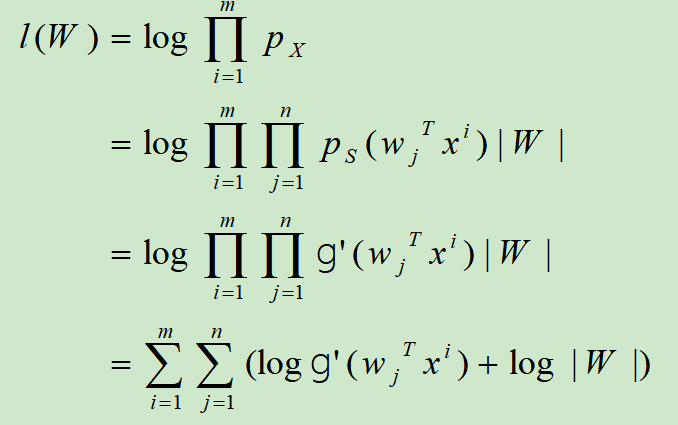
根据$\nabla_{W}|W|=|W|(W^{-1})^{T}$，我们将其最大化，并可以导出如下的随机梯度上升学习规则：
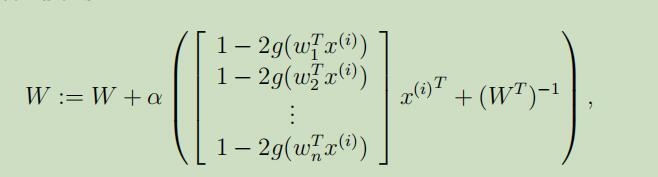
α为学习速率
在算法收敛时，我们计算$s^{(i)}=W x^{(i)}$就可以恢复出我们的源s。
Remark： 当我们给出以上的似然函数时，我们假设$x^{(i)} \mathrm{s}$是相互独立的（不同于$x^{(i)}$中的每个坐标独立），所以训练集的似然函数为$\prod_{i} p(x^{(i)} ; W)$。当$x^{(i)} \mathrm{s}$是依赖时（比如说讲话的数据，时间序列）这种假设就不再是正确的，但它并不会在我们拥有充分多数据的情况下损伤算法的性能。而且，在拥有连续的相关数据集是，这将会加快SGA算法的收敛。
