视频地址：https://www.bilibili.com/video/av49432977/?p=16 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes12.pdf
Lecture 16 - Reinforcement Learning and Control
对于一些需要作出序列性决定和控制的问题，很难提出一种监督学习的方法来解决问题，在强化学习框架中我们将为我们的算法仅提供一个反馈函数，来暗示当前啊的决策是“好”，还是“坏”。这样可以使得学习算法的任务转换到解决怎样随着时间选择一系列动作来达到最大的反馈这个问题。
我们对强化学习的研究将先从Markov decision processes (MDP) 开始，其可以将常见的RL问题给形式化。
Markov decision processes (MDP)
一个马尔科夫决策过程具有五个属性的元组，其中：
- S是状态的集合
- A是动作的集合
- $P_{sa}$是状态转移概率
- $\gamma \in[0,1)$是折扣因子
- $R : S \times A \mapsto \mathbb{R}$是反馈函数
MDP处理中的属性变化如下： 从状态$s_0$开始，选择一些动作$a_{0} \in A$来进行MDP。作为结果，MDP的状态会随机的变化到下一个状态$s_1$，其中$s_{1} \sim P_{s_{0} a_{0}}$。然后，我们选择另一个动作$α_1$，状态再一次的改变，现在变成了状态$s_{2} \sim P_{s_{1} a_{1}}$。。。。
我们也可以将这个处理过程描绘如下：
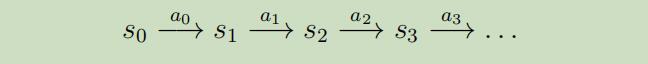
继而，我们的总共得到的报酬 为：
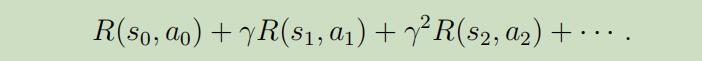
或者，我们把反馈函数的参数简写为仅根据状态，总共报酬 可以变为：
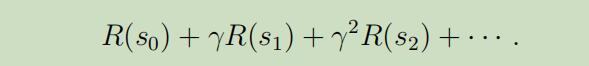
我们在强化学习中的目标 为随着时间相应的选择一些动作，来最大化总共报酬的期望值
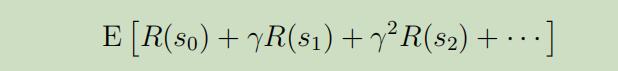
注意到在每个时间点t我们所获得的反馈会被因子$\gamma^{t}$（一般取值0.99附近）给打折扣，拖得时间越久，当前获得的反馈折扣的力度就越大。因此我们需要尽可能快的增加正向反馈，以此来最大化期望
一项政策（policy可以是任意的映射函数$π$：从状态$S$映射到一定的动作$A$。 我们也可以说成，当我们在某一状态$s$时，如果我们执行某一政策$π$，我们将采用动作$a=\pi(s)$。 同样的，我们可以将某一特定政策$π$的价值函数 定义为：
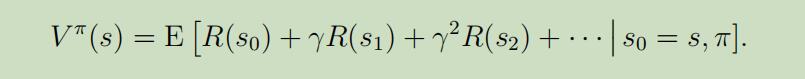
这里插入一下Bellman等式 ：当给定一个固定的政策$π$时，它的价值函数$V^{\pi}$满足如下等式：
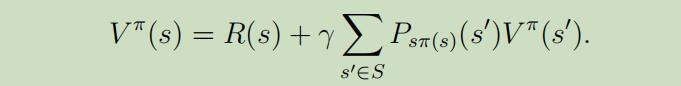
以上等式由两项组成：第一项，即时反馈$R(s)$表示从状态s开始获得的即时反馈，第二项为未来折扣反馈的期望和。
更详细些，第二项可以被写为，在第一步之后的第二步所有可能状态的反馈期望$\mathrm{E}_ {s^{\prime} \sim P_{s \pi(s)}}[V^{\pi}(s^{\prime})]$的和。
Bellman等式可以有效的去解出$V^π$ ， 特别是在有限状态集MDP中，我们可以为其中的每一个特状态s都写出其等式$V^{\pi}(s)$，这个等式会产生$|S|$个新的等式，把这些等式当做为方程组（$|S|$个变量和$|S|$个方程组），就可以被高效的解出。
我们定义最优价值函数 为：
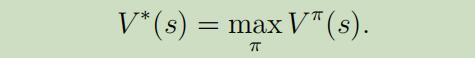
BEllman等式 版本的最优价值函数为 ：
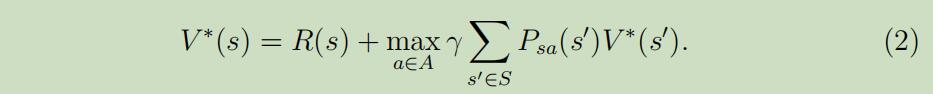其中第一项仍然是之前的即时反馈，第二项是 在第一步后的所有动作的未来折扣反馈的最大值（相当于多了一层对动作a的循环，并取其最大值）。
我们定义政策$\pi^{*} : S \mapsto A$如下：
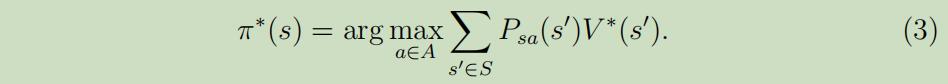即能使上式子最大化的参数a。
对于每个状态s和政策π，有如下事实：
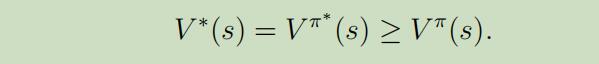
而且$\pi^{\ast}$具有一个有趣的属性，就是它是对所有的状态s最优的策略 ，意味着我们可以使用相同的政策$\pi^{\ast}$无论MDP的初始状态是啥。
价值(value)迭代和政策(policy)迭代
在这部分，我们将介绍两种高效地解出有限状态MDP的算法。从现在起，我们将只考虑有限状态和有限动作空间($|S| < \infty$ ,$|A|<\infty$)的MDP。
第一个算法，价值迭代 ：
- 对于每个状态s，初始化为$V(s) :=0$
-
重复直到收敛｛
对于每个状态，做如下更新$V(s) :=R(s)+\max _ {a \in A} \gamma \sum_{s^{\prime}} P_{s a}(s^{\prime}) V(s^{\prime})$
｝
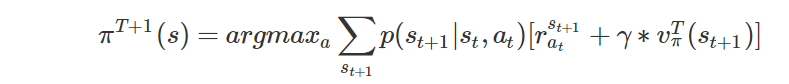这个算法可以被看作为 重复的尝试去使用Bellman等式来更新估计的价值函数。
这里由两种可能的方法来执行内层的更新程序：同步和异步。
同步更新： 首先为每个状态s计算$V(s)$的新值，然后用这些新值来全部重写旧值。在这种方式中，这个算法可以被看做实施了一次“Bellamn 备份操作（见课后作业）”，其采用当前价值函数的估计值并映射到新的估计值。
异步更新 ：以某种顺序一次更新一个
无论是使用同步或者异步更新，都显示出价值迭代会使$V$收敛到$V^*$，当找到$V^\ast$时，我们可以利用等式（3）来找出最优的政策。
第二种算法，政策迭代，可以找到MDP中一个最优的政策：
https://www.cnblogs.com/huangyc/p/10381184.html
因此，内层的循环将会重复地为当前的政策计算价值函数,直至价值收敛，然后使用当前的价值函数来更新政策,直至政策收敛，然后再使用所得的政策重新进行步骤（2） （在步骤（3）中要寻找的$π$也被称作关于$V$的贪婪政策）。注意这里步骤(2)可以使用Bellman等式来解出，对于一个固定的政策需要计算$|S|$个变量组成的$|S|$的线性方程组。
在这个算法执行完有限轮的迭代 后，$V$将收敛到$V^\ast$，并且$π$将收敛到$π^\ast$
价值迭代和政策迭代都是解决MDP的标准算法 ，但是当前并没有对到底哪个算法更好一点达成统一的认知。对于小规模状态空间的MDP，政策迭代通常会用非常少的迭代来达到快速收敛，然而对视大鬼魅状态空间的MDP，求解$V^{\pi}$将会涉及大规模的线性方程组，这求解起来会比较的困难，对于这类问题价值迭代会更好些。
DMP的模型学习
我们之前讨论的都是假设已知状态转移概率和反馈函数的情况下的MDP算法，但是在很多实际问题中，我们可能并没有事先知道具体的状态转移概率和反馈 ，所以我们反而需要去从数据中来估计出这些未知值。（通常，S,A,γ已知）
举个例子，假设对着这个**反转钟摆问题（inverted pendulum problem，见作业4），在MDP中我们有如下的流程：
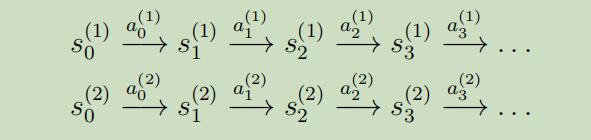其中，$s_{i}^{(j)}$为在时间i所做实验的状态，并且$a_{i}^{(j)}$是在这个状态下相对应的动作。
当给定这些由许多实验组成的MDP中的“经验”时，我们可以容易的导出状态转移概率的极大似然估计：
注意，如果上面的概率为“0/0”–等同于在状态s下从来不采取动作a–我们可以简单的估计$P_{s a}(s^{\prime})$为1$/|S|$（例如这里估计$P_{s a}$对于所有状态都服从均匀分布）
使用相同的程序，如果R未知的话，我们也可以采用我们估计的期望即时反馈$R(s)$来为s下的平均反馈。
这时我们可以使用价值迭代或者政策迭代，和估计的转移概率和反馈，来求解出MDP 。例如，将模型学习和价值迭代放在一起后的算法如下:
- 随机初始化$π$
- 重复｛
(a) 在MDP中执行$π$来进行多个试验
(b) 使用在MDP中积累的经验，来更新我们对$P_{sa}$的估计(如果可以的话，还有R)
(c) 根据估计的模型参数，应用价值迭代来得到新的价值函数V的估计
(d) 更新$π$使其成为越来越贪婪的政策
｝
注意到在这个算法中做了一些小改进，在内层的价值迭代中并没有初始化V=0，而是将其初始化为前一轮迭代的解，这将会为价值迭代提供一个更好的起始点，并能够更快速的收敛
