coursera公开课视频地址：https://www.coursera.org/learn/neural-networks-deep-learning? 课程主页地址：http://cs230.stanford.edu/
Introduction
因为我网上已经找到了很好的课程笔记，我觉得自己也没有必要再自己写一遍了，所以之后就不再更新了。笔记地址：https://baozoulin.gitbook.io/neural-networks-and-deep-learning/
吴恩达老师的cs230公开课的讲述形式和之前的cs230公开课有些不同，采用的是ppt教学，不像之前cs229直接提供文字版讲义。这样就导致在编写课程笔记的时候，不会像cs229那时可以直接根据讲义来写，所以在这部分cs230的笔记中，我将会根据自己的基础和理解来挑选出自己觉得重要的知识点记录推导下来，知识点可能会具有一定的跳跃性，但仍能确保自己以后可以根据这份笔记理清深度学习的脉络。ppt等资源在课程主页上提供的都有，所以这里也就不再次提供了，需要的可以自己去下载。
Lecture 1 -Shallow neural networks
这之前我们介绍了逻辑回归的神经网络模式，可以大概的理解到了神经网络的运行模式。点击前往
下面就让我们来推导出一遍浅层神经网络是从何而来的。
浅层神经网络模型
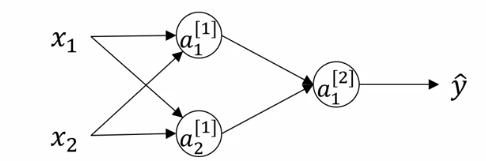
下图为单个样本情况下的一般化的浅层神经网络的模型，通常我们称这个模型具有两层（隐藏层和输出层），隐藏层为第1层，输出层为第2层。
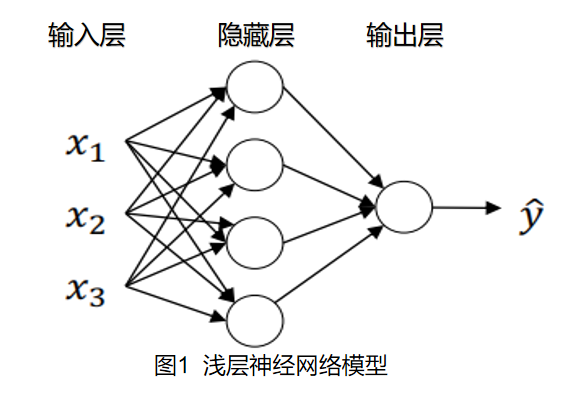
图中每个圆圈称作为神经元，每个神经元都具有自己相应的隐藏变量，神经元左半部分接受输入参数进行计算，右半部分用于对处理计算结果并输出为下一层神经元的参数。
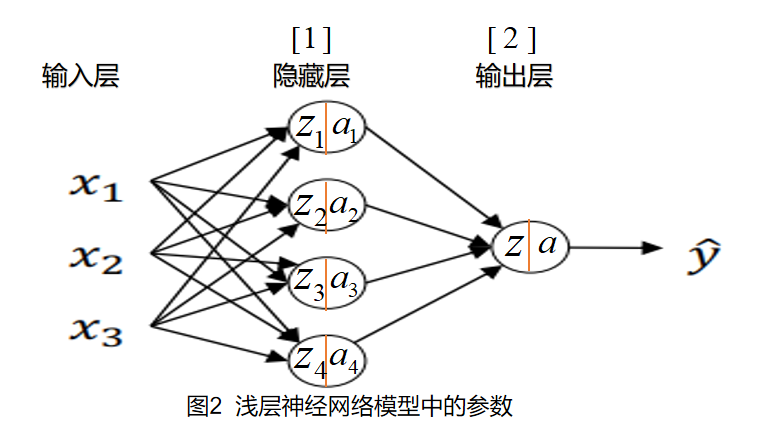
每层神经元的参数我们可以用$W$和$b$来表示，上标$[1]$表示是第几层的参数。 例如：$z_1^{[1]}=w_1^{[1]T} x+b^{[1]},a_1 = \sigma (z)$为第1层第1个神经元的计算结果，它的参数为$w_1^{[1]}$和$b^{[1]}$。
推广开来可以得到第一层和第二层的计算： \(\begin{array}{l}{z^{[1]}=W^{[1]} x+b^{[1]}} \\ {a^{[1]}=\sigma(z^{[1]})} \\ {z^{[2]}=W^{[2]} a^{[1]}+b^{[2]}} \\ {a^{[2]}=\sigma(z^{[2]})}\end{array}\)
注意此时计算的不再是单个神经元，而是以一个层来计算，此时的参数变为了 \(W^{[1]}=[\begin{array}{ccc}{-} & {w_{1}^{T}} & {-} \\ {-} & {w_{2}^{T}} & {-} \\ {-} & {w_{3}^{T}} & {-} \\ {-} & {w_{4}^{T}} & {-}\end{array}]\)
$z^{[1]}$和$a^{[1]}$现在均变成了$4 \times 1$的列向量。第二层的参数$W^{[2]}$是$1\times4$的行向量。参数$b^{[1]}$和$b^{[2]}$均为实数，但可以通过广播参与每个神经元的计算。
多样本浅层神经网络模型
上面描述的是只有一个样本的情况下，浅层神经网络的运作模式，在有多个样本时，我们该怎么做呢？ ： 答案就是，将每个样本都进行通过一次神经网络计算，然后将每个样本的计算结果堆叠起来。
现在我们将每个样本按列排放： \(X=[\begin{array}{ccc}{ |} & { |} & {} & { |} \\ {x^{(1)}} & {x^{(2)}} & {\cdots} & {x^{(m)}} \\ { |} & { |} & {} & { |}\end{array}]\) 此时第一层的计算就同样的$Z^{[1]}$的每一列都为相应样本的$z^{[i]}$。： \(Z^{[1]}=W^{[1]}X+b^{[1]}=[\begin{array}{ccc}{ |} & { |} & {} & { |} \\ {z^{[1](1)}} & {z^{[1](2)}} & {\cdots} & {z^{[1](m)}} \\ { |} & { |} & {} & { |}\end{array}]\tag 1\)
同样的， \(A^{[1]} = [\begin{array}{ccc}{ |} & { |} & {} & { |} \\ {a^{[1](1)}} & {a^{[1](2)}} & {\cdots} & {a^{[1](m)}} \\ { |} & { |} & {} & { |}\end{array}] \tag 2\) 第二层同理，$Z^{[2]}$和$A^{[2]}$变为： \(\begin{array}{l}{Z^{[2]}=W^{[2]} A^{[1]}+b^{[2]}} \tag 3\\ {A^{[2]}=\sigma(Z^{[2]})}\end{array}\)
公式(1)(2)(3)就是多样本时神经网络的计算公式。
神经网络的反向传播
我们的单样本时的神经网络模型，可以简单的描绘出如下的形式：
其中损失函数为：
\(L(a,y)=-\lbrace yloga+(1-y)log(1-a) \rbrace\)
我们可以依次根据反向传播，计算出每个参数的梯度：
\(\begin{array}{l}{d z^{[2]}=a^{[2]}-y} \\ {d W^{[2]}=d z^{[2]} a^{[1]^{T}}} \\ {d b^{[2]}=d z^{[2]} } \\ {d z^{[1]}=W^{[2] T} d z^{[2]} * g^{[1]^{\prime}}(\mathbf{z}^{[1]})} \\ {d W^{[1]}=d z^{[1]} x^{T}} \\ {d b^{[1]}=d z^{[1]}}\end{array}\)
然后我们可以利用随机梯度下降等算法来对参数进行更新。
但是在具有多个样本时，我们就需要对上述梯度进行向量化处理，这是就使得神经网络能够一次训练多个样本，而不仅仅是一个样本。
其相应的向量化处理为：
激活函数的选择
（1）sigmoid
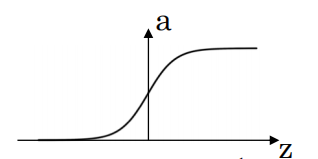\(\text { sigmoid: } a=\frac{1}{1+e^{-z}}\)
（2）tanh
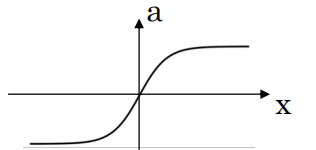\(\tanh : a=\frac{a^{z}-e^{-z}}{e^{z}+e^{z}}\)
$g(z)^\prime = 1 - tanh(z)^2$
sogmoid 函数和 tanh 函数的 一个共同缺点是 如果 z 很大或者很小 那么这个函数的梯度或者导数 或者斜率将会很小 所以如果 z 非常大或者非常小 那么该函数的斜率将最终接近 0 然后会减慢梯度下降的速度。但是sigmoid的均值为0.5，tanh的为0。所以相对来说，tanh比sigmoid常用一些。sigmoid除了在二分类时很少使用
（3）RELU
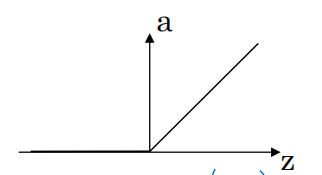\(\text { Relu } \quad a=\max (0,z)\)
(4)Leaky RELU
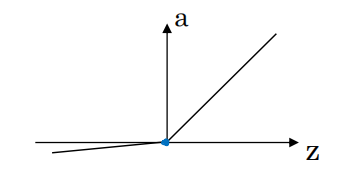\(\text {Leaky Relu } \quad a=\max (0.01z,z)\)
使用 ReLU 和 leaky ReLU 的优点是 对于大部分的 z 空间, 激活函数的导数, 或者激活函数的斜率不会为 0 所以, 在练习中使用 ReLU 激活函数 你的神经网络的学习速度 将通常比使用 tanh 函数 或者 sigmoid 函数要快得多 。
随机初始化
为什么要随机初始化？首先看一下参数初始化为0时，会发生什么状况。
\(W^{[1]}=\left[\begin{array}{ll}{0} & {0} \\ {0} & {0}\end{array}\right],
b^{[1]}=\left[\begin{array}{l}{0} \\ {0}\end{array}\right]\)
这时隐藏层第一个神经元计算结果为$z_1^{[1]} = w_1^Tx+b=0$，第二个单元$z_2^{[1]} = w_2^Tx+b=0$，这样最后的得到的梯度$dz_1^{[1]} = dz_2^{[2]}$，所以最后更新所得到的的$z_1^{[1]}和z_2^{[2]}$将会一样的。所以这样往复下去，两个神经元的计算功能将会是一样的。这称之为神经元的对称性，且会一直保留下去。
那怎么样随机初始化呢？ 可以令参数矩阵 $W^{[1]} = np.random.randn((2,2))*0.01$
参数b初始化为0即可。$W^{[2]}$同理
为什么要乘以0.01呢？因为在使用sigmoid和tanh为激活函数的情况下，参数W过大，将会导致$z= w^Tx+b$的变大，使得z在经过激活函数时的斜率会变得很小，极大地降低了学习的速度。
