Deeplearning之CNN类型总结
一.经典网络
1. LeNet-5
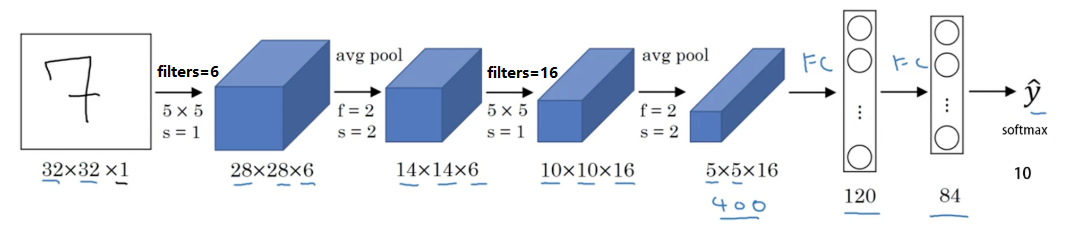
性质:
- 针对灰度图片训练的,所以图片的大小只有32×32×1
- 包含大约6w个参数
- 现在一般使用 ReLU 作为激活函数,输出层一般选择 softmax。
2. AlexNet
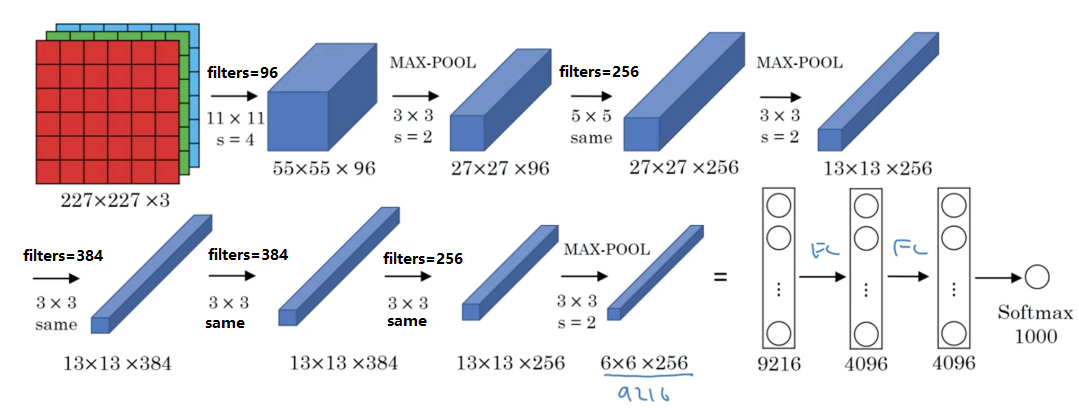
性质:
- 约6000w个参数
- 激活函数为 RELU
3. VGG-16
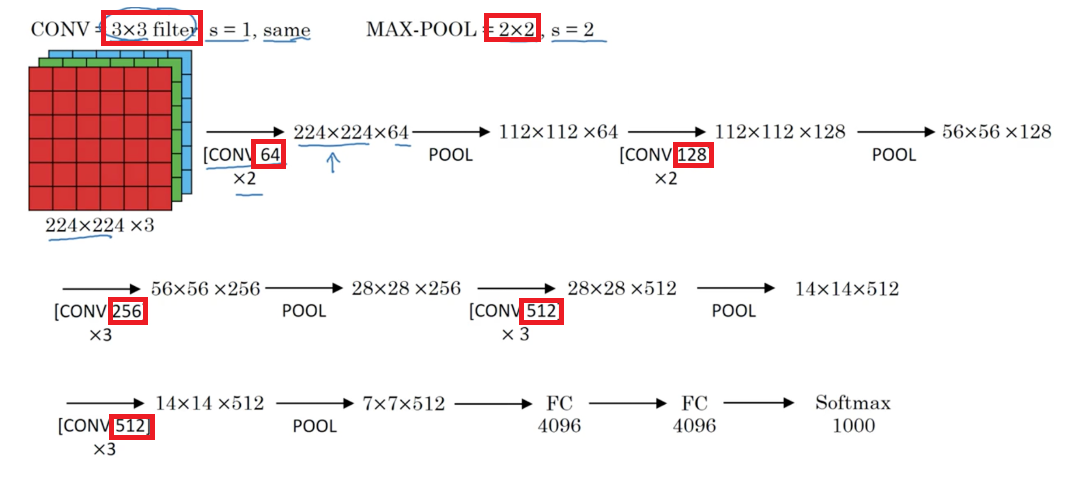
性质:
- 简化了神经网络结构,1.38亿个参数
- 网络结构非常规整,卷积层大小都为$3 \times 3$,且逐步将通道数扩大一倍;池化层大小都为$2 \times 2$,用来逐步缩小图像尺寸一倍。
- VGG-16中的16代表,可以训练的层数为16层(卷积层+FC层+softmax层)
- 缺点是,需要训练的特征数量非常巨大
二.深度卷积网络
1. 残差网络(ResNet-50)
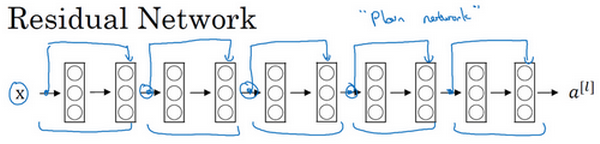
残差单元示意图:
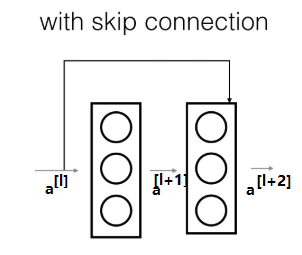
上图中上方的线,可以称作为神经网络层的跳跃连接,此模块可以被称为残差块,作用为弱化每层之间的强联系,建立隔层之间的联系,这样能够很有效的将之前层的信息继续传递下去。
$a^{[l]}$与$a^{[l+2]}$之间隔层联系的表达式为: \(a^{[l+2]}=g\left(z^{[l+2]}+a^{[l)}\right)\)
一般RetNet的网络结构如图:
ResNet-50的网络结构如图: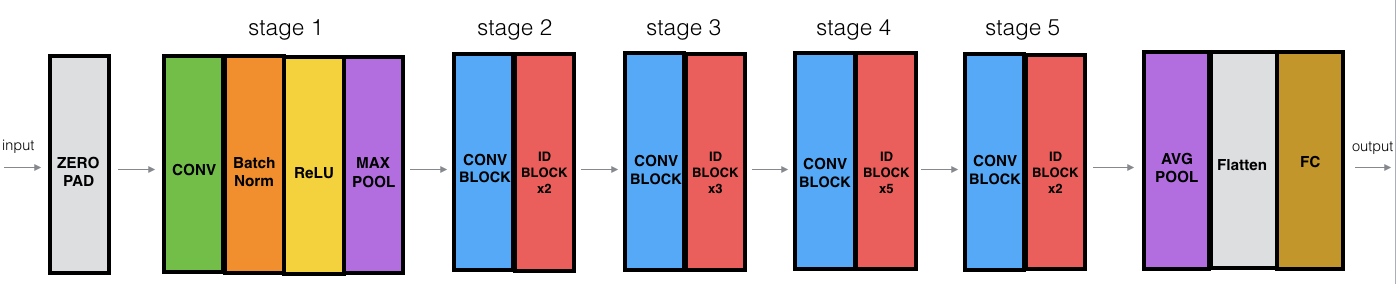
其中“ID BLOCK”为“Identity block”,意味着和前一个卷积层结构一样。
其详细的结构如下:
- 阶段一
-
- 卷积层,大小为$7 \times 7$的64个filters,$strides = (2,2)$
-
- 最大池层,大小为$3 \times 3$,$strides = (2,2)$
- 阶段二
-
- 3层卷积层,大小为$3 \times 3$,每一层filters的数量分别为$[64,64,256]$
-
- 2个ID BLOCK,规模和前一卷积块一样
- 阶段三
-
- 三层卷积层,大小为$3 \times3$,$strides=(2,2)$,每一层的filters的数量分别为$[128,128,512]$
-
- 3个ID BLOCK,规模和前一卷积块一样
- 阶段四
-
- 三层卷积层,大小为$3 \times 3$,$strides=(2,2)$,每一层的filteres的数量分别为$[256,256,1024]$
-
- 5个ID BLOCK,规模和前一卷积块一样
- 阶段五
-
- 三层卷积层,大小为$3 \times 3$,$strides = (2,2)$,每一层的filters的数量分别为$[512,512,2048]$
-
-
2个ID BLOCK,规模和前一卷积块一样
-
为什么残差网络可以很深? \(a^{[l+2]}=g\left(z^{[l+2]}+a^{[l)}\right)=g\left(W^{[l+2]} a^{[l+1]}+b^{[l+2]}+a^{[l]}\right)\) 观察上式,当我们进行L2正则化时,权值$W^{[l+2]}$会变得非常得小,在深层网络很容易发生梯度消失问题,这就使得层次越深,训练效果越不好。我们现在可以直接假设发生了梯度消失,即$ W^{[l+2]} \approx 0, \quad b^{[l+2]} \approx 0 $,此时$[l+2]$层的激活值为$g(a^{[l]})$非负。相当于直接忽略了之后的这两层神经层。这样看似很深的神经网络,由于许多Residual blocks的存在,弱化削减了某些神经层之间的联系,实现隔层线性传递,而不是一味追求非线性关系,模型本身也就能“容忍”更深层的神经网络了。
若残差块中的$a^{[l]}$和$a^{[l+2]}$的维度不同,怎么办?
-
- padding补0
-
- 引入矩阵$W_s$与$a^{[l]}$相乘,使其维度与$a^{[l+2]}$一致
-
- 将$W_s$作为学习参数,通过模型训练得到
-
- 固定$W_s$的值,不够补0
2.谷歌 Inception
Inception单元如图:
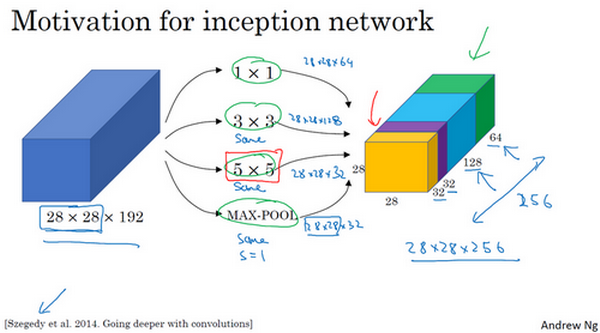
基本思想: 适用多个不同尺寸或者不同类型的filters,进行same填充,将每一类过滤器的卷积结果叠加起来,由神经网络来决定使用那些filters,并学习得到最好的参数。
性质:
- 不需要人工来确定卷积层中的 过滤器类型,和是否需要创建卷积层或者池化层。
- 所有的filters都需要进行same填充
- 计算量巨大,可以使用$1 \times 1$的卷积进行减少计算量
目标检测
1. YoLo算法
首先将图像划分为$3 \times 3$或$19 \times 19$的网格,每一个网格的标签集为$y = [p_c,b_x,b_y,b_h,b_w,c_1,c_2,c_3]$
 再加上2个锚盒时,每个网格会有两个标签集或者说,这两个标签集的连接。
再加上2个锚盒时,每个网格会有两个标签集或者说,这两个标签集的连接。
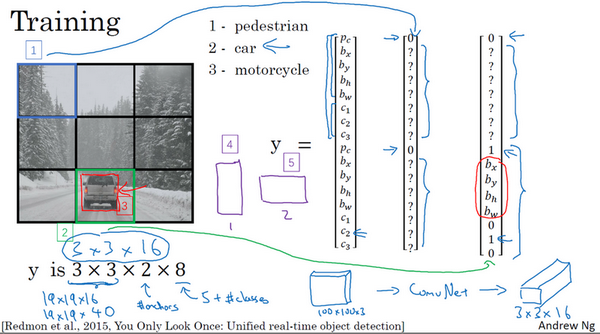
如果要训练一个输入为$100 \times 100$的网络,先将输入图像经过普通的卷积神经网络,例如卷积层、池化层等,最后映射到$3 \times 3 \times 2 \times 8$或者$3 \times 3 \times 16$的输出尺寸。其中每个$3 \times 3$的小方格都对应输入图像相对应位置的网格的标签。
最后再运用非极大值抑制算法来获得最好的定位框。
优点:
- 并没有在3×3网格上跑9次算法,而是单次卷积实现,但在处理这3×3计算中很多计算步骤是共享的,所以这个算法效率很高
- 显式地输出边界框坐标,可以具有任意宽高比,并且能输出更精确的坐标,不会受到滑动窗口分类器的步长大小限制
- 因为是卷积实现,运行速度非常快,可以达到实时识别
2.R-CNN算法
R-CNN算法首先使用K-Means聚类算法,对图像进行聚类处理,在每个色块上进行处理,然后再分类。
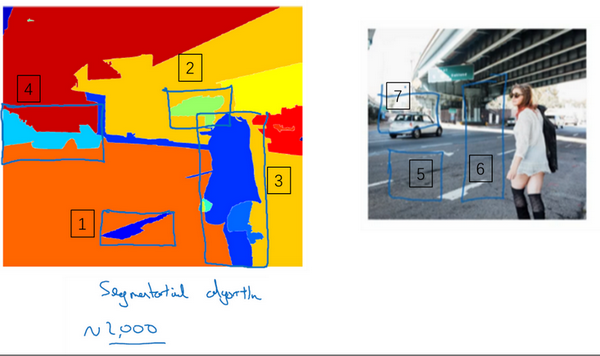
缺点:
- 算法运行速度很慢,每次分类前都需要对图像进行处理。
Fast R-CNN Fast R-CNN算法基本上是R-CNN算法,最初的算法是逐一对区域分类,快速R-CNN用的是滑动窗法的一个卷积实现,显著提升了R-CNN的速度,问题是得到候选区域的聚类步骤仍然非常缓慢
Faster R-CNN 更快的R-CNN算法(Faster R-CNN),使用的是卷积神经网络,而不是更传统的分割算法来获得候选区域色块,比Fast R-CNN算法快得多。 不过大多数更快R-CNN的算法实现还是比YOLO算法慢很多