视频地址：https://www.bilibili.com/video/av41393758/?p=4 课程主页地址：http://web.stanford.edu/class/cs224n/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/CS224n/cs224n-2019-notes03-neuralnets.pdf
Lecture 4 - Natural Language Processing with Deep Learning
1 神经网络基础
我们为什么需要神经网络?
这一部分，吴恩达的DeepLearning课程已经讲得很详细了，这里就略写一下。
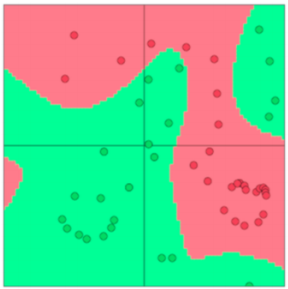
因为如果数据集是线性不可分的，那么我们就需要非线性的分类器，使用机器学习中的线性分类器将会限制我们所能达到的性能。现在让我们看如果来使用神经网络创建非线性的决策曲线。
1.1 神经元
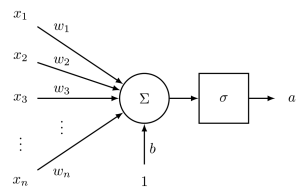
对于一个单个神经元来说，它的输入是n维特征，其具有一个n为权重向量参数w，和一个偏差值。 当这个神经元的激活函数是’sigmoid’时，我们可以得到这个神经元的输出为：
\[a=\frac{1}{1+\exp (-(w^{T} x+b))}\]单个神经元的神经网络示意图如下：
1.2 单层神经网络
假设我们的神经网络只有一个隐藏层，这个隐藏层中具有m个神经元
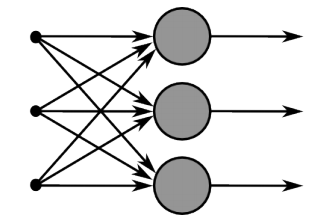和之前一样，我们将每个神经元的参数定义为：
权重$\lbrace w^{(1)}, \cdots, w^{(m)}\rbrace$和偏差$\lbrace b_{1}, \cdots, b_{m}\rbrace$，他们各自的激活函数为$\lbrace a_{1}, \cdots, a_{m}\rbrace$： \(\begin{aligned} a_{1} &=\frac{1}{1+\exp (w^{(1) T} x+b_{1})} \\ \vdots & \\ a_{m} &=\frac{1}{1+\exp (w^{(m)T} x+b_{m})} \end{aligned}\)
我们可以用向量化表示为：
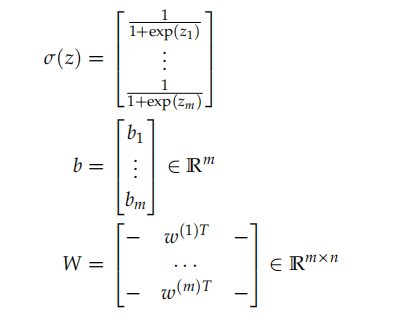
此时的sigmoid函数可以被写为： \([\begin{array}{c}{a^{(1)}} \\ {\vdots} \\ {a^{(m)}}\end{array}]=\sigma(z)=\sigma(W x+b)\)
1.3 前馈计算
让我们考虑NLP领域中的如下命名实体识别问题： \(\text {"Museums in Paris are amazing" }\) 在这里，我们想要去分类中心词“Paris”是否是被命名的实体，在这种情况下，我们就不仅仅想捕捉窗口中的词是否出现而产生的词向量，更像来捕捉每个词之间的相互关系来进行分类，而捕捉这种复杂的非线性关系就需要用到神经网络。
因此，我们使用另一个矩阵$U \in R^{m \times 1}$来对一个分类任务生成非正式化的评分：
\(s=U^{T} a=U^{T} f(W x+b)\)
其中，f是激活函数。
1.4 最大边距目标函数
假设我们将正确样本的分数标记为$s$，将错误样本的分数标记为$s_c$，因此我们希望预测正确的概率大于预测错误的概率，即$s>s_c$，但我们希望预测能够更加的自信，所以希望$s-s_c > 1$。 这样就可以导出我们的目标函数：\(\text { minimize } J=\max (1+s_{c}-s, 0)\)
Lecture 5 - Back Propagation
这一部分的内容我觉得没有啥必要再把深度学习里的东西搬过来，所以这里就不再叙述
Lecture 6 - dependency-parsing
这一部分的内容，没接触过没太懂，下面这篇博客写的已经很详细了。http://www.hankcs.com/nlp/cs224n-dependency-parsing.html
Lecture 7 - TensorFlow入门
同样，一直在用的东西，所以视频就没看了，想直接看一些干货。
