视频地址:https://www.bilibili.com/video/av41393758/?p=9 课程主页地址:http://web.stanford.edu/class/cs224n/ 课程讲义下载地址:https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/CS224n/cs224n-2019-notes05-LM_RNN.pdf
Lecture 9 - GRU and LSTM
1. Gated Recurrent Units
因为循环神经网络具有无法捕捉深层的连接关系,且就有梯度消失的可能性,这里的GRU单元改变了传统的RNN隐藏层结构,使其可以更好地捕捉深层连接,并改善了梯度消失问题。
1.1 GRU单元的前向传播
一个GRU单元的表达式为:
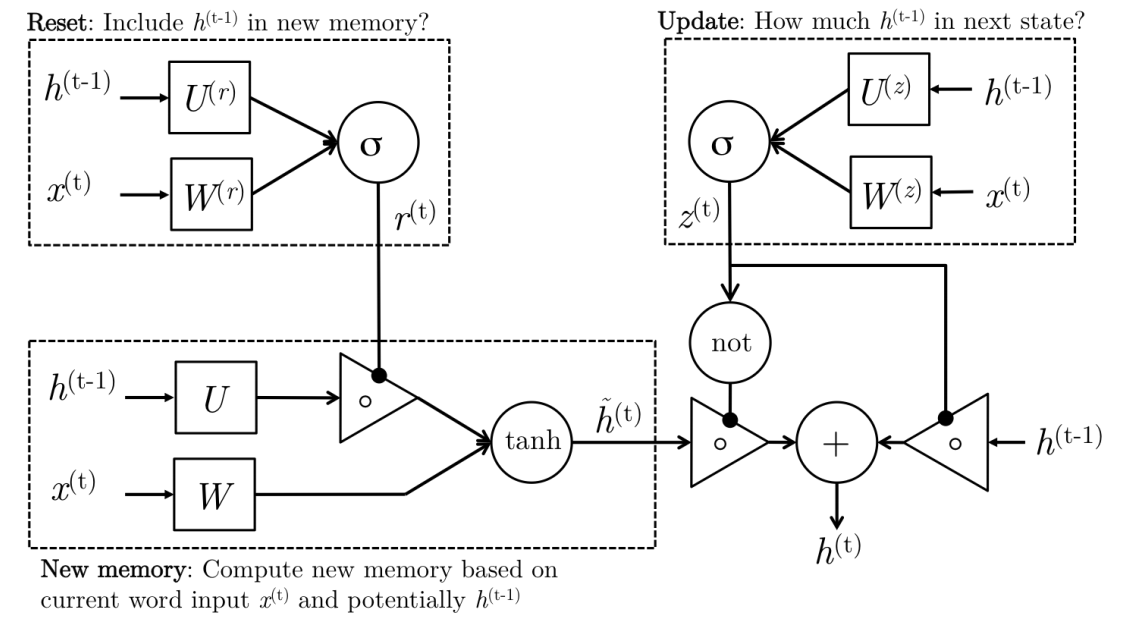
\(\Gamma_{u}=\sigma\left(W_{u}\left[c^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{u}\right) \tag{update门}\) \(\Gamma_{r}=\sigma\left(W_{r}\left[c^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{r}\right) \tag{reset 门}\) \(\tilde{c}^{\lt t \gt}=\tanh \left(W_{c}\left[\Gamma_{r} * c^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{c}\right) \tag{new memory门}\) \(c^{\lt t \gt}=\Gamma_{u} * \tilde{c}^{\lt t \gt}+\left(1-\Gamma_{u}\right) * c^{\lt t-1 \gt} \tag{activate 门}\) 其中$a^{\lt t \gt}=c^{\lt t \gt}$。 其中每个门的具体作用为:
- Update 门: 更新信号$\Gamma_u$决定了上一隐藏层的状态$c^{\lt t-1 \gt}$有多少应当传递到下一状态$c^{\lt t \gt}$中,即是否进行更新。例如,如果$z_{t} \approx 1$,那么$c^{\lt t-1 \gt}$将近完全带入到下一状态中;如果$z_{t} \approx 0$,那么新的记忆单元$\hat c^{\lt t \gt}$将会传递到下一状态里。
- Reset 门: 重置信号$\Gamma_r$决定了上一状态$c^{\lt t-1 \gt}$有对于新的记忆单元$\hat c^{\lt t \gt}$的重要性。如果reset门发现过去的隐藏层状态和当前新的记忆单元没有关系,其完全可以消除过去的隐藏层状态$c^{t-1}$。
- New memory 门: 是上一隐藏层传递的状态和新的输入词$x^{\lt t \gt}$之间的结合。更形象的说,通过联合上一隐藏层状态$c^{\lt t-1 \gt}$和当前输入词$x^{\lt t \gt}$的影响,用来来生成新的隐藏层的状态。
GRU单元更形象的结构图为:
1.2 GRU单元的反向传播
2. LSTM(Long-Short-Term-Memories)
长短期记忆单元是另一类复杂的激活单元,其在结构上和GRU单元有些小小的不同,其具有更加强大的记忆能力和抗梯度消失能力。
2.1 LSTM单元的前向传播
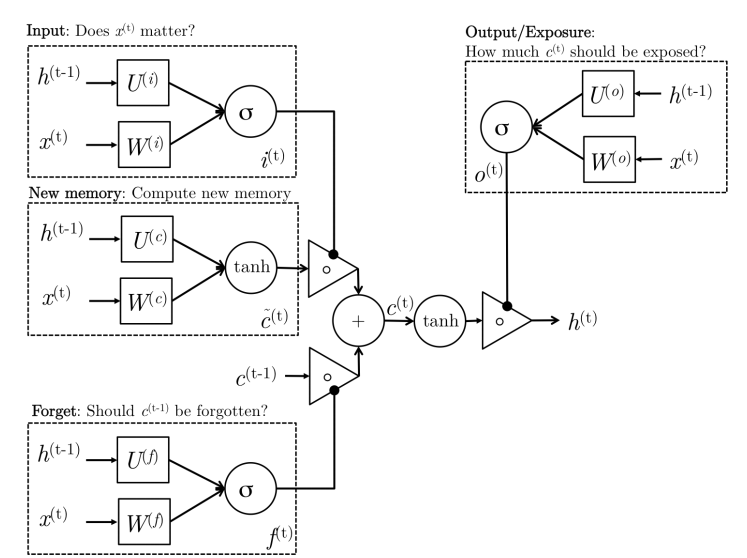
一个LSTM单元的前向传播表达式为: \(\begin{array}{ll}\tilde{c}^{\lt t \gt}=\tanh \left(W_{c}\left[a^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{c}\right) &\text {(new memory门)} \\ \Gamma_{i}=\sigma\left(W_{u}\left[a^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{u}\right) &\text {(input 门)} \\ \Gamma_{f}=\sigma\left(W_{f}\left[a^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{f}\right) &\text{(forget 门)} \\ c^{\lt t \gt}=\Gamma_{i} * \tilde{c}^{\lt t \gt}+\Gamma_{f} * c^{\lt t-1 \gt} &\text{(final memory 门)} \\ \Gamma_{o}=\sigma\left(W_{o}\left[a^{\lt t-1 \gt}, x^{\lt t \gt}\right]+b_{o}\right) &\text{(output 门)} \\a^{\lt t \gt}=\Gamma_{o} * c^{\lt t \gt} \end{array}\)
其中每个门的具体作用为:
- New memory generation: 与GRU类似,使用当前词语$x^{\lt t \gt}$ 和之前的隐状态$a^{\lt t-1 \gt}$来生成新的记忆$\hat c^{\lt t \gt}$。于是新记忆里面就包含了当前词语$x^{\lt t \gt}$的属性。
- Input Gate:: 使用当前词语和之前的隐状态决定当前词语是否值得保留用来产生new memroy 门的新记忆,这个“是否”是通过$\Gamma_i$来体现的
- Forget Gate:和Input Gate类似,只不过它不是用来衡量输入单词的有用与否,而是衡量过去的记忆对计算当前记忆有用与否。 它接受输入单词和上一刻的隐状态产生输出 $\Gamma _f$。
- Final memory generation:根据Input Gate的建议决定保留多少新产生的记忆$\hat c^{\lt t \gt}$,根据forget Gate的建议决定忘掉多少过去得记忆$c^{\lt t-1 \gt}$
- Output Gate: 在GRU中不显示存在,其作用是将final memory$c^{\lt t \gt}$和隐藏层的状态$a^{\lt t-1 \gt}$分离开来。因为final memory可能包含了很多不是那么重要的信息,没有必要全传递到下一隐藏层状态$a^{\lt t \gt}$中去,因此它根据$a^{\lt t \gt}$需要那一部分的$c^{\lt t \gt}$,从而来进行分配。
LSTM单元的网络结构
3. 如何处理大词汇表问题
尽管如今的翻译系统已经取得了不错的成绩,但是存在一个问题,就是通常需要大量的时间来计算由很大的词汇表造成的softmax计算问题。
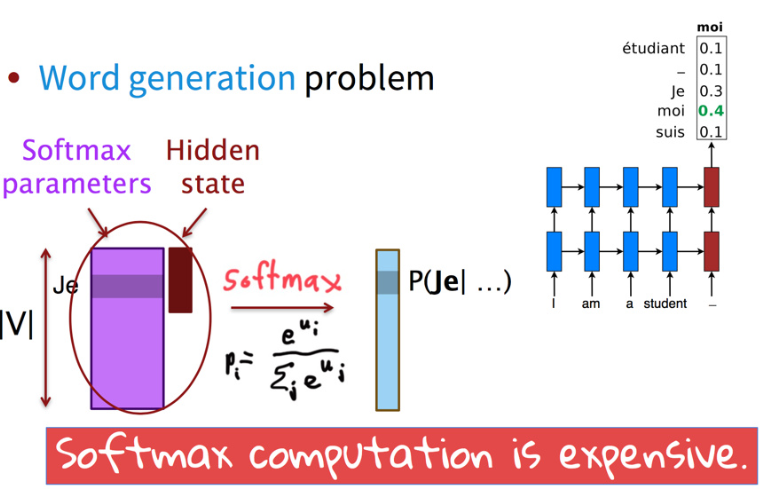
3.1 scaling softmax
直觉告诉我们说,有没有什么更加有效的方法来让我们计算布标的概率分布?当然有,下面两种方法可以有效的降低softmax 的复杂度:
- Noise Contrastive Estimation 随机从负样本中选取K个词来估计softmax,说白了就是负采样。
- Hierarchical Softmax 建立一颗Huffman树,可以使算法的复杂度降低到$ O(\log |V|) $。但是不能有效的在GPU上并行化。
这两种方法都是词嵌入中采用的方法,但是在这里应用有个共同的缺点,就是仅能在训练的时候减少softmax的计算量,在测试时,这两种方法无法使用。
3.2 Reducing vocabulary
将训练样本分割成每个包含了目标词的大小为$\tau=\left|V^{\prime}\right|$的子集,子集可以通过对原始训练集进行顺序扫描,直到子集包括了$\tau=\left|V^{\prime}\right|$个词。这样的思想有点类似于负采样,因为它包含了一个目标词,和$\left|V^{\prime}\right|-1$个负样本,其主要的差异在于,这些负样本都是从一个有偏重的分布Q中采集获得:
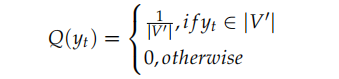

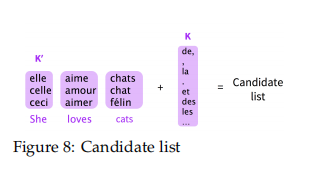
在测试的时候,我们可以从整个词汇表中挑选出一个候选列表,候选列表可以有K个最常出现的词和$K’$个原句子中最相近的词组成。如: