请咨询作者同意后转载。
Scalable Graph-based Bug Search for Firmware Images(Genius)
项目地址：https://github.com/qian-feng/Gencoding
| 期刊/会议： | CCS（A类） |
|---|---|
| 发表时间： | 2016年10月24日 |
| 发表机构： | Syracuse University |
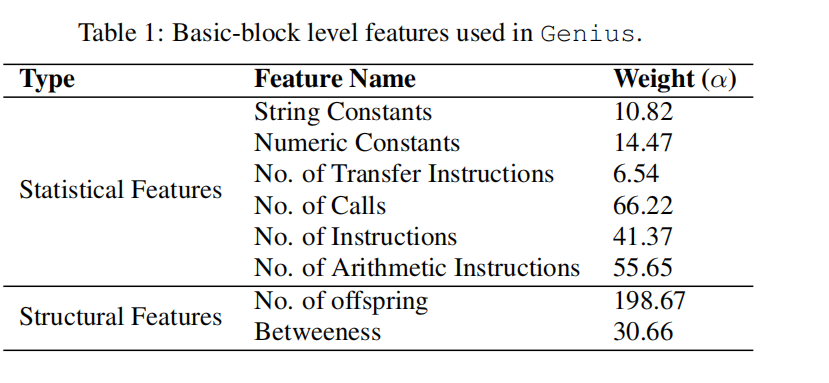
属性控制流图
在这篇文章中，属性控制流图考虑如下的两种特征：统计上的和结构上的
受到复杂网络的启发，本文采用两种类型的结构特征：no.of offspring 和betweenness。
- no.of offspring为控制流图中孩子节点的数量，它可以帮助我们定位一个节点在图中的第几layer。
- betweenness centrality可以给出一个节点在图中的中心程度。
具体实现
1.编码本生成
1.1 原生特征相似性生成
定义：编码本$C$是一个有限且离散的子集$\mathcal{C}=\left \lbrace c_{1}, c_{2}, \ldots, c_{k}\right \rbrace$，其中$c_i$是第i个编码词。
在这里，我们将原生特征相似性计算转化为二分图匹配问题，而二分图匹配利用两个图的匹配代价作为其相似性的计算，通过将匹配代价建模为一个优化过程来对匹配代价进行量化。
给定两个ACFGS，G1和G2，将其合并成一个二分图$G_{b p}=(\hat{V}, \hat{E})$，其中$\hat{V}=V\left(G_{1}\right) \cup V\left(G_{2}\right)$， $\hat{E}=\left\lbrace\hat{e}_ {k}=\left(v_{i}, v_{j}\right) | v_{i} \in V\left(G_{1}\right) \wedge v_{j} \in V\left(G_{2}\right)\right\rbrace$。我们称$\hat{e}_ {k}=\left(v_{i}, v_{j}\right)$为v1到v2的一个匹配，每个匹配都与一个代价相关联,而两个图之间的最小匹配代价 就是在此映射上所有匹配边边的代价之和。二分图匹配算法可以有效的帮助我们遍历所有可能的匹配映射，并未$G_1和G_2$选择出具有最小代价的一对一的匹配映射。
二分图的最佳完美匹配——KM算法 https://blog.csdn.net/sixdaycoder/article/details/47720471
在此问题中，ACFG中的基本块就是二分图的节点，每条边的代价就是每个节点之间的距离，而ACFG的每个节点可以表征成数字向量的形式，因此两个基本块之间的代价可以通过如下公式进行计算：
\[\operatorname{cost}(v, \hat{v})=\frac{\sum_{i} \alpha_{i}\left|a_{i}-\hat{a}_ {i}\right|}{\sum_{i} \alpha_{i} \max \left(a_{i}, \hat{a}_{i}\right)}\]当特征是集合时，我们可以使用jacard来计算集合的差。$\alpha_i$为ACFG中每个特征的权重（除了选取的特征集和不同外，这与DiscovRe中的block distance定义几乎一样）。
如前面所述，二分图匹配算法的输出为两个图的最小匹配代价，通常来说两个图的匹配代价大于一个图，并且与被比较的ACFG的size呈正相关。因此对于每个被比较的ACFG作者使用空的ACFG $\phi$来对代价计算进行标准化，在empty graph中的每个节点都有一个空的特征向量，并且大小与被比较图的大小一样。通过与empty graph作比较，我们可以得到被比较图最大的代价(其实就是basic block的个数)，来进行标准化。此时两个图$g_1和g_2$的相似性计算公式如下：
\[\kappa\left(g_{1}, g_{2}\right)=1-\frac{\operatorname{cost}\left(g_{1}, g_{2}\right)}{\max \left(\operatorname{cost}\left(g_{1}, \Phi\right), \operatorname{cost}\left(\Phi, g_{2}\right)\right)}\]这里需要注意的是，ACFG中属性的权重是通过学习获得的，我们希望我们学习的权重能够捕获ACFGs之间的潜在相似性特征，更基本的说，我们的目标函数找到的参数既可以最大化不同ACFGs之间的距离，也能最小化相似ACFGs之间的距离。
权重学习所使用的方法：Eschweile[23]，遗传算法：GALib[56] 参考文献：[23] S. Eschweiler, K. Yakdan, and E. Gerhards-Padilla. discovre: Efficient cross-architecture identification of bugs in binary code. In NDSS, 2016 [56] M. Wall. Galib: A c++ library of genetic algorithm components. Mechanical Engineering Department, Massachusetts Institute of Technology, 87:54, 1996
1.2 聚类
这里使用谱聚类方法来根据相似性对原生特征进行聚类。谱聚类算法将ACFGs的训练集划分为n个集合$\mathcal{S}=\left\lbrace S_{1}, S_{2}, \ldots, S_{n}\right\rbrace$来最小化每个ACFG到其聚类中心之间的距离，而每个子集$S_i$的聚类中心$c_i$的集合就是我们所需要的编码本。
这里需要注意的是，在谱聚类中经过相似嵌入后获得的是相似矩阵的拉普拉斯矩阵最小特征值的$k_1$个特征向量形成的矩阵$H:n\times k_1$，通过对$H$按行进行kmeans聚类得到$k_2$个聚类中心，而且$k_2$个聚类中心是特征向量聚类得到的，不代表图中的任一个节点，也不适用与节点之间的相似性度量。
所以，作者将聚类中心节点$c_i$定义为ACFG中，它与$S_i$中所有其他ACFG具有最小的距离，这意味着$c_i$需要我们自己算出。
谱聚类 https://www.cnblogs.com/pinard/p/6221564.html sklearn 谱聚类 https://www.cnblogs.com/pinard/p/6235920.html
但与传统聚类算法不同的是，这里的输入不是数字向量，而是kernel 矩阵，假设我们的kernel矩阵为M，那么M中的每个元素为其对应ACFGs的相似度。
同时，为了降低计算复杂度，从整个数据集中随机取样一个训练集进行训练。并且该过程可以线下进行。
2. 特征编码
所谓特征编码，就是给定编码本时，将函数的原生特征映射到高维度数字向量，并且每一维度都保留了每一类别之间的相似距离。
特征编码的优点如下： 1.更高层次的特征可以更好的容忍不同平台见函数的变化。 2.编码后的ACFG原生特征变成了高维空间中的一个点，这可以让我们更方便的是使用hash方法来索引和搜寻。
形式化的说，特征编码就是要在编码本$\mathcal{C}=\left\lbrace c_{1}, \ldots, c_{n}\right\rbrace$上学习一个量化器(quantizer)$q: \mathbb{G} \rightarrow\mathbb{R}^{n}$。这里我们给出两种方法来导出q：对于一个给定的图$g_{i}$，令$N N\left(g_{i}\right)$表示编码本中与其最近的中心邻居（可以是k个与其最近的邻居）：
\[N N\left(g_{i}\right)=\arg \max _ {c_{i} \in \mathcal{C}} \kappa\left(g_{i}, c_{j}\right)\]Bag-of-feature encoding.
\[q\left(g_{i}\right)=\sum_{g_{i}: N N\left(g_{i}\right)=c_{j}}[\mathbb{1}(1=j), \ldots, \mathbb{1}(n=j)]^{T}\]VLAD encoding. bog-of-word模型的缺点是给定图和中心的距离完全忽略了,而VLAD则弥补了这个缺点：
\[q\left(g_{i}\right)=\sum_{g_{i}: N N\left(g_{i}\right)=c_{j}}\left[\mathbb{1}(1=j) \kappa\left(g_{i}, c_{1}\right), \ldots, \mathbb{1}(n=j) \kappa\left(g_{i}, c_{n}\right)\right]^{T}\]下面举个例子来说明VLAD encoding。
(a)为F1在x86和mips下编译得到的控制流图，以及另一个函数F2在mips下编译得到的控制流图。
(b)为经过训练所得到的的编码本。
(c)为使用图匹配算法对(a)中的三个控制流图进行匹配得出的相似性结果，可以看出其预测结果存在较大的偏差。
(d)为VLAD encoding在不同距离度量标准下的相似性分数，可以看出在欧几里德距离下能够区分出相同与不相同的函数。
在线搜索
经过特征编码后的特征可能直接被用来进行搜索，但是这样的方法可能并不能扩展到具有上百万函数的真是世界中，因此我们采用LSH方法。
LSH方法可以学习得到一个投影：如果两个点在特征编码空间中距离很近，那么其在hash空间中的投影也很近。给定编码后的特征$q(g)$，我们将投影函数$h_i$定义如下：
\[h_{i}(q(g))=\lfloor(\mathbf{v} \cdot q(g)+b) / w\rfloor\]其中w是quantized bin的大小，v是从高斯分布中随机选取的向量，b为0-w之间的随机变量。
编码后的特征$q(g)$的LSH值为$lsh(g)=\left[h_{1}(q(g)), \ldots, h_{w}(q(g))\right]$，经过LSH后，一个函数就是被投影到hash空间中的一个点。
LSH https://blog.csdn.net/guoziqing506/article/details/53019049/ MinHash原理 https://www.jianshu.com/p/535c537a5766
实验评估
1.实验设置
写了个IDA的插件用来生成ACFG。使用Nearpy来LSH，MongoDB来存储固件镜像和编码后的特征。24核心，2.8GHZ，65GB内存，2TB硬盘的服务器。
2.数据集准备
数据集1-Baseline evaluation：用于baseline比较。标准设置：
| dataset | architectures | compiler versions | optimization levels |
|---|---|---|---|
| BusyBox(v1.21 and v1.20) | x86 | gcc v4.6.2/v4.8.1 | O0-O3 |
| OpenSSL (v1.0.1f and v1.0.1a) | ARM | clang v3.0 | |
| coreutils(v6.5 and v6.7) | MIPS |
数据集2-Public dataset：有其他人采用两个公开数据集，所以本文也加上这些数据集来公平的比较。
数据集3-Firmware image dataset：从其他地方寻找到的33045个固件镜像，使用这些来测试Genius的可扩展性。
数据集4-The vulnerability dataset:具有CVE编号的漏洞数据集，用来构建一个查询。因为其他的数据集在这里并不可用，所以此文创建了一个数据集。
3.跨平台Baseline比较
Evaluation metrics： 使用召回率和假正率来测试我们的baseline方法。例如，对于每个查询q，在总共L个函数中匹配到了m个函数，我们认为top-K个检索到的函数为正例，正确匹配的函数个数为$\mu$为真正例，剩下的$K-\mu$为假正例。所以我们可以计算得到召回率为recall$(q)=\frac{\mu}{m}$，假正率为$F P R(q)=\frac{(K-\mu)}{L-m}$。
Baseline 系统的建立 ：使用三个具有代表性且先进的跨平台bug搜索技术来建立我们的评估baseline：discovRe，Multi-MH and Multi-k-MH ，a centroid based search
Accuracy 比较： 从baseline数据集中随机选取了1000个函数进行查询。
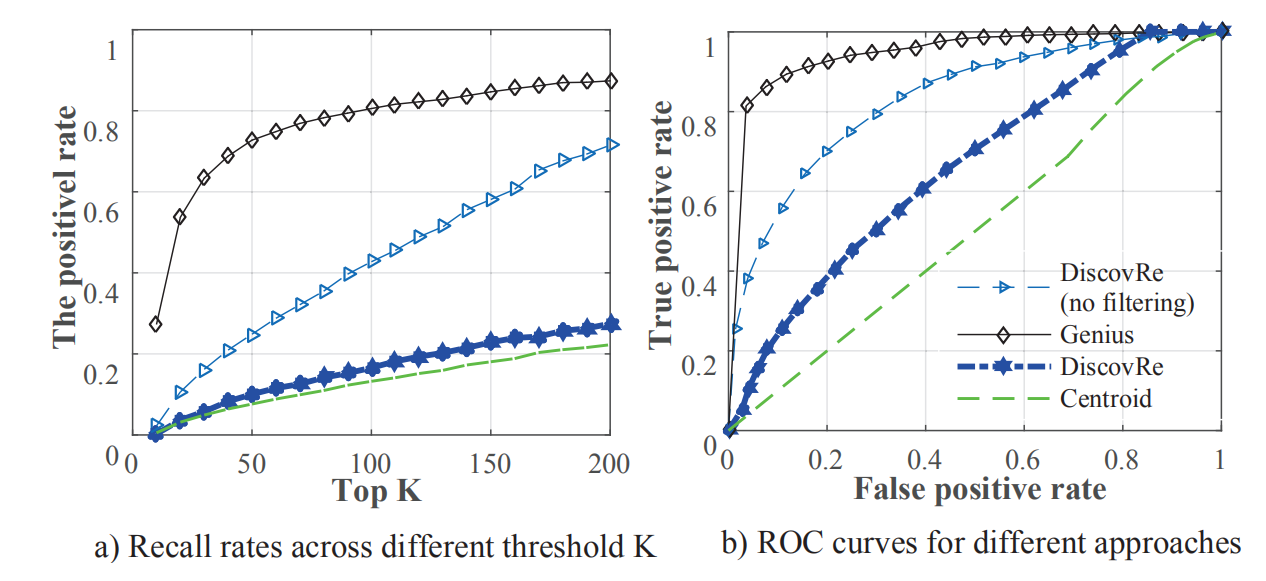从图中可以看出Genius方法相较于baseline方法实现了更高的Accuracy。
分析：Genius取得如此好的性能的主要原因在于其高层次和健壮的特征，不会轻易因为平台的改变而发生改变。但分析其性能不如baseline的例子发现，其原因可能是学习得到的编码本的质量不行。
Efficiency 比较：
线下预处理比较：
在线搜索时间比较：
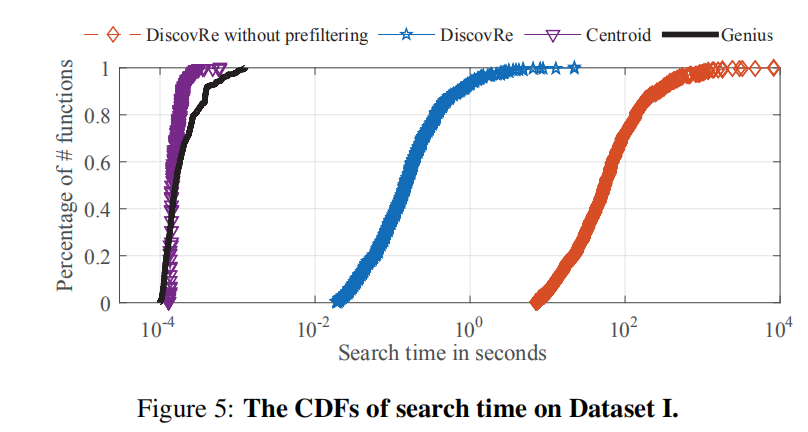
分析：相对来说Genius和Centroid取得了较好的效率，但是为了能够提高准确率，可以牺牲一部分时间来进行线下预处理，即使Centroid线上搜索效率比Genius好，但相比而言我们看重的应当是准确率。
4.参数学习
通过实验，来进行参数评估，结果如下：
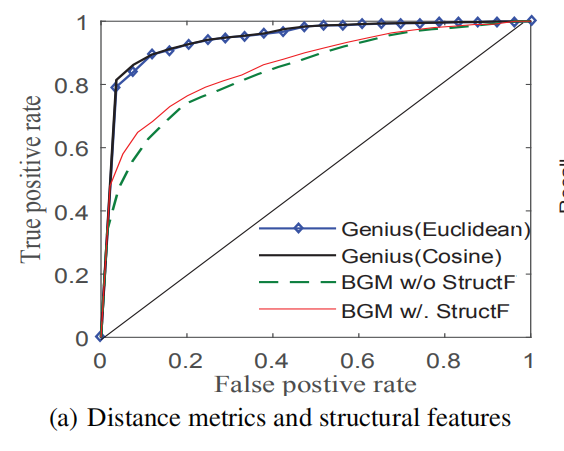
A.Distance metrics and structural features：
有Structural features会更好，余弦相似度会比欧几里德距离好。
B.编码本大小：
编码本的大小对准确率额影响并不是很大，因此我们倾向与选取小的size来降低预处理的时间。
C.训练集大小： 生成编码本所采样的训练集大小，是个很重要的参数，越大准确度越高，但当10w个函数时就已足够。
D.Feature encoding method 毫无置疑，VLAD方法更好。
6.案例学习
场景1：在数据集3上使用从数据集4中提取出的2个CVE漏洞函数进行查询，在top50中确认了23个存在漏洞的函数。 场景2：寻找两个最新的镜像，并使用数据集4中所有154个漏洞函数进行查询，在top100中确认了16个存在漏洞的函数。 证明了Genius在真实环境中寻找漏洞的能力。
Discussion
存在的问题：
- 高度依赖CFG提取的质量，可以考虑比IDA更好的CFG提取工具
- 内联函数会影响CFG流程。
- Genius受CFG的大小影响较大，因为越小的CFG月可能发生碰撞
