请咨询作者同意后转载。
αDiff: Cross-Version Binary Code Similarity Detection with DNN
github :https://twelveand0.github.io/AlphaDiff-ASE2018-Appendix
| 期刊/会议： | ASE（A类） |
|---|---|
| 发表时间： | 2018年11月 |
| 发表机构： | 中科院 |
1.前言
该方法主要针对跨version二进制检测问题：在源代码自身随着时间进行更新后，产生了跨版本的二进制，这些二进制仅在语法结构和语义上有轻微的差别。
主要思想：
- 使用DNN在函数的Byte层面提取函数内特征
- 分析函数调用图，提取函数间特征
- 统计导入函数，提取模块间特征
- 基于以上三个语义特征计算距离
研究问题： 针对人工定义特征引入的偏差，本文研究的第一个问题是：
- RQ1：如何从二进制代码中提取尽可能少的人类偏差的特征。
针对BinGo和Esh对CFG片段语义相似性严格的检查和计算代价的昂贵，本文研究的第二个问题是：
- RQ2：如何有效地利用语义特征来提高BCSD的准确性？
针对BinDiff在跨长版本时准确率的急剧下降，本文研究的第三个问题是：
- 本文提出的第三个研究问题是：RQ3：如何建立一个适合跨版本的BCSD的解决方案？
2.问题定义
BCSD的一个核心任务就是为每一个函数寻找匹配。如果两个函数编译后的函数名相同且具有相似的上下文，那么可以考虑这两个函数为一个匹配。
2.1 跨版本BCSD问题定义
(1)函数匹配：对于每个在binary $B_1$中的函数$f_{1i}$，如果存在，在binary $B_2$中寻找它的匹配$f_{2j}$
(2)相似性分数：为函数对$f_{1i},f_{2j}$计算0-1之间的相似性分数来表征其相似度
(3)差异识别：如果函数对$f_{1i},f_{2j}$之间的相似性分数小于1，找出其在代码比特层面的不同。
本篇本章主要针对的是前面两个问题，但是在实验中发现，此方法在跨平台二进制相似性检测上也能取得很好的效果。
2.2 评估指标
计算TopK的召回率：Recall@K。
3.方法介绍
3.1 概述
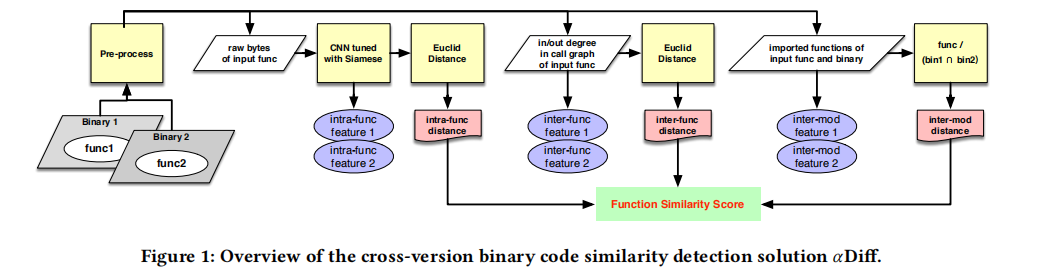如图1所示：
- 输入两个二进制的函数，提取函数的Byte流输入到CNN Siamese网络中，输出两个函数的特征向量和距离
- 根据两个函数的调用图得出函数间特征向量，并计算其距离
- 根据两个函数的导入函数得到模块间特征向量，计算距离
- 根据上面计算的三个距离，综合得出两个函数的相似性分数
3.2 函数内语义特征
将函数转化成比特流后，作者尝试了很多网络(Conv1d,LSTM,ConvLSTM..)，最后醉着发现CNN最适合来提取函数的语义特征。
为了能够满足相似性准则，我们采用Siamese网络结构，使得相似的函数特征之间的距离小，相似性低的函数特征之间距离大。
CNN网络结构： 8卷积层，8 batch normaliztion层，4 maxpooling 层，2 全连接层，所有的激活函数都是用RELU，参数有160w。
CNN的输入： 提取二进制函数的比特流，若超过1w字节则截断，不足则拿0填充。将这1w的字节流转换成$100\times 100 \times 1$的张量作为CNN的输入。
1w比特已经足够判断两个函数是否相似了。
函数特征距离度量：
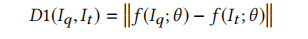
Siamese网络的损失函数：
其中$m$为提前定义好的超参数，用来决定我们期望不相似的函数之间至少应当有多大的距离。
负采样： Siamese需要大量的正样本和负样本。正样本可以通过对同一项目不同版本的源代码编译得到，对于负样本，需要在训练中每个mini-batch基于正样本来生成。
例如对于一个mini-batch中的每个正样本$(I_q,I_p)$，我们生成两个semi-hard负样本，$(I_q,I_{n1})和(I_p,I_{n2})$。以函数$I_q$为例，我们将随机挑选一个函数$I_{n1}$满足如下约束：
\(0< D1(I_q,I_n) < m\) 但是我们也要跳过那些最难训练的负样本，例如$argmin D1(I_q,I_n)$，因为这些样本会使模型陷入坏的局部极小值。
3.3 函数间语义特征
作者根据 相似的函数具有相似的函数调用图，从而在函数调用图中提取相似性特征。
因为函数相互调用、递归等存在，使得对整个函数调用图处理代价太过于昂贵。所以作者只采集函数的入度节点和出度节点来作为函数间特征。例如，对于函数$I_q$，我们将其函数间特征定义为如下的二维向量：
\[g(I_q) = (in(I_q),out(I_q))\]其中$in(I_q)$和$out(I_q)$分别为函数$I_q$在调用图中的入度和出度。
3.4 模块间语义特征
作者发现相似的函数会调用相似的导入函数，并在版本的变化当中相对稳定。
为了一致性，我们将模块间特征也转化为向量来用于距离计算，其计算公式如下：
\(h(set,superset) = < x_1,x_2,...,x_N >\) 其中$N$为超集的大小，如果super中的第i个元素在set中，那么$x_i = 1$
对于两个函数$I_q$和$I_t$，假设它们的二进制程序为$B_q$和$B_t$，我们可以得到它们的导入函数集合$imp(B_q)$和$imp(B_t)$。我们使用$imp(B_q) \hat imp(B_t)$作为superset，然后可以得到这两个函数的距离为：
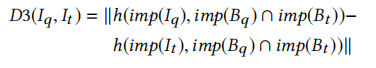
3.5 整个相似度计算
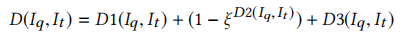
因为跨版本的二进制中，函数调用图可能会发生较大的变化，我们希望函数间特征在最后的相似性计算中起的作用小一些，所以就增加了一个0-1的超参数。
