Asm2Vec:Boosting Static Representation Robustness for Binary Clone Search against Code Obfuscation and Compiler Optimization
https://github.com/McGill-DMaS/Kam1n0-Plugin-IDA-Pro
| 期刊/会议： | CCS |
|---|---|
| 发表时间： | 2019年5月 |
| 发表机构： | McGill University |
一.前言
本文中提出了一种较为新颖的指令嵌入模型，能够较好的对抗代码混淆和编译器的优化选项。
首先，作者较为全面的指出二进制代码相似性搜寻的应用场景：
- 定位二进制中发生变化的部分
- 识别已知库函数
- 寻找已知程序漏洞
- 检测侵犯GNU条例的软件剽窃
其次，作者指出了代码混淆和优化选项会破坏控制流和基本块的完整性，这就意味着结构特征和语法特征完全混淆了，使得语法相似性的检查会更加的困难。
同时，作者还指出了之前方法面临的两个问题：
- 之前的方法都假设每个特征都是一个独立的维度。但是比如说，SSE寄存器(xmm0)通常和SSE操作(movaps)相关，fclose调用通常和fopen相关，这些关系提供了很多的语义。为此，作者提出了利用词条之间的共现关系来发现丰富的词法语义关系。
- 对于需要先验知识的问题，作者提出训练神经网络模型来读取许多汇编代码数据，并让自动模型识别最佳的表征和区分函数的不同。
二.总体工作流程
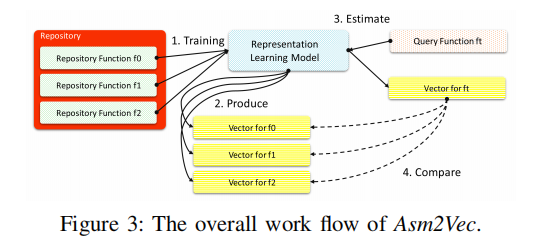
Step1: 给定一仓库的汇编函数，将其当做训练集搭建神经网络模型进行无监督训练。
Step2：训练阶段完成后，会为每个仓库中的函数产生一个向量表示。
Step3：给定一个未训练过的目标函数$f_t$，使用模型估计其向量表示。
Step4：计算$ft$向量和仓库中其他函数的向量的预先相似度，并返回topk个作为候选结果。
三.汇编代码表征学习
因为作者的方法是基于PV-DM模型，并在PV-DM模型上进行了改进，使得其可以处理像图这类的结构化数据。
3.1 预备知识
PV-DM模型是为文本数据设计的，是word2vec模型的一种扩展，其可以对每个短词和段落学习lianhe向量表示。其模型结构如图所示：
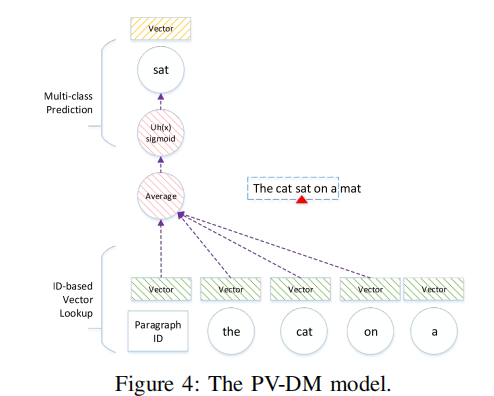
可以看出来和word2vec中的CBOW模型很像，给定包含一系列段落的语料$p$的语料$T$，每个段落$p$包含一系列的句子$s \in p$，并且每个句子由一系列的单词组成$w_t \in s$。其对应的需要最大化的目标函数就为
\[\sum_{p}^T \sum_{s}^{p} \sum_{t=k}^{|s|-k} \log \mathbf{P}\left(w_{t} \mid p, w_{t-k}, \ldots, w_{t+k}\right) \tag 1\]3.2 Asm2Vec 模型
模型图如下：
首先，我们映射每个仓库中的函数$f_s$到一个向量$\vec \theta_{f_s} \in R^{2\times d}$，且这个向量表示$\vec \theta_{f_s}$会在之后的训练过程中来学习。我们将汇编代码中的操作码和操作数看成为词条，并映射每个词条$t$到一个数字向量$\vec v_t \in R^d$和另一个数字向量$\vec {v’_t} \in R^{2 \times d}$。其中$\vec v_t$为词条$t$具有的词法和语义的向量表示，向量$\vec {v’_t}$用来做词条的预测。
刚开始时$\vec \theta_{f_s}$和$\vec v_t$都被初始化为很小的随机数，$\vec {v’_t}$被初始化为0。
下面给出之后会用到的一些符号表示：
这里我们就采用PV-DM模型的思想：给定一条在函数$f_s$中的指令序列$seq_i$，从序列$seq_i$的开始遍历每条指令（忽略边界的两条指令），对于当前指令$in_j$来说，其上下文指令分别为$in_{j-1}$和$in_{j+1}$，所以根据PV-DM模型，我们需要最大化的目标函数为：
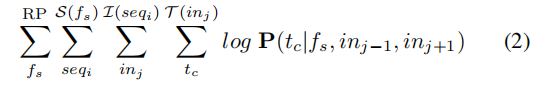
这样做的直觉是使用当前函数的向量和邻居指令提供的上下文来预测当前指令。邻居指令提供的向量可以捕捉词法语法关系，而函数向量则可以记忆在给定段落和上下文情况下同一指令的不同概率，并可以在建模的过程中区分当前函数和其他函数。
对于上图，形式化的来说，给定一个函数$f_s$，我们首先在提前建立好的字典中寻找其向量表示$\vec \theta_{f_s}$。为了对邻居指令 $in$ 建模为$2\times d$的向量，我们需要将每个操作数$A(in)$的向量$\vec v_{t_b}$进行累加平均，并和操作码$P(in)$的向量$\vec {P(in)}$进行串联，从而得到上下文指令的向量： \(\mathcal{C T}(i n)=\vec{v}_ {\mathcal{P}(i n)} \| \frac{1}{|\mathcal{A}(i n)|} \sum_{t}^{\mathcal{A}(i n)} \vec{v}_ {t_{b}} \tag 3\)
随后，我们可以得到对于当前指令$in_j$来说，在函数$f_s$中其上下文的记忆的建模表示： \(\delta\left(i n_{j}, f_{s}\right)=\frac{1}{3}\left(\vec{\theta}_{f_{s}}+\mathcal{C} \mathcal{T}\left(i n_{j-1}\right)+\mathcal{C} \mathcal{T}\left(i n_{j+1}\right)\right) \tag 4\)
现在目标函数(2)就可以重写为，如下的形式： \(\mathbf{P}\left(t_{c} \mid f_{s}, i n_{j-1}, i n_{j+1}\right)=\mathbf{P}\left(t_{c} \mid \delta\left(i n_{j}, f_{s}\right)\right) \tag 5\)
因为，对于每个词条来说，具有两个向量$\vec v$和$\vec {v’}$，之前$\vec v$被我们用来生成上下文，这里我们使用$\vec {v’}$来进行预测，可以将公式(5)中的概率建模为多分类问题：
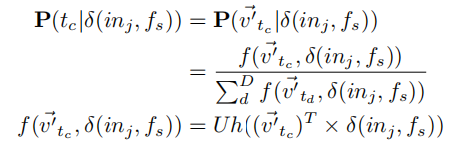其中$Uh(*)$表示sigmoid函数。
但是如果$|D|$很大的话，会严重降低计算的效率，所以我们继而采用负采样的方法来估计上面的log概率：
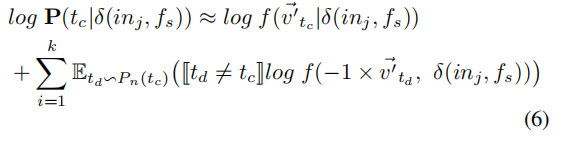其中$E_{t_d \sim P_n(t_c)}$为一个采样函数，根据噪声分布$P_n(t_c)$从词汇表D中取样一个词条$t_d$。
更新公式如下：
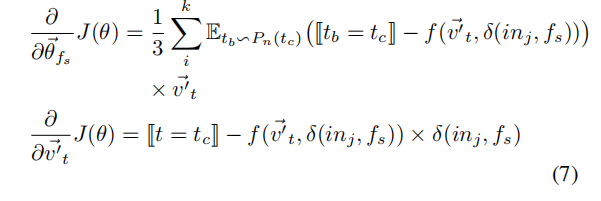
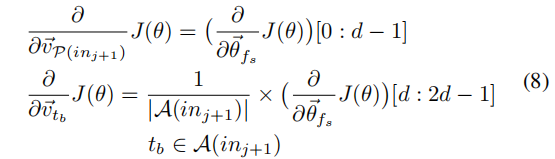
3.3 为汇编函数建模
因为控制流图原先的线性布局覆盖了很多的无效执行路径，所以我们不能直接使用作为训练序列，相反的，我们将控制流图建模为边集覆盖序列和随机游走。
3.3.1 选择性内联
-
BinGo内联所有的标准库函数调用，希望能够获得正确的语义。但是我们并不需要内联任何的库函数调用，因为我们的模型已经能够很好地捕捉库调用词条中的词法语义信息。
-
BinGo会递归的内联被调用的函数，但是这样做可能会导致调用者函数中包含了太多的被调用函数的代码，导致调用者函数的语义功能和被调用的函数的功能更为相似。所以我们这里只在函数调用图中扩展一阶的被调用函数。
在判断一个用户函数是否需要内联，采用了和BinGo一样的耦合度度量指标和阈值，但是如果callee函数长于或和caller一样长，那么callee就会占用caller的大部分代码比列，因此，作者添加了额外的指标来过滤那些过于长的callee。 \(\delta\left(f_{s}, f_{c}\right)=\operatorname{length}\left(f_{c}\right) / \text { length }\left(f_{s}\right)\)
3.3.2 边覆盖
从经过上面内联扩展后的控制流图中随机采样边，直到原来的控制流图中所有的边都被覆盖。每条边相连的两个基本块中的指令作为训练使用的指令序列。
这样做的目的是，即使控制流图被分裂或合并，我们也可以得到相似的指令序列。
3.3.3 随机游走
我们从扩展后的控制流图中添加很多的随机游走，来扩展我们获得的指令序列。
这样做的目的是，一些起主要作用的基本块通常在控制流图的必经路径上，多次随机游走就有很大的概率来采样到这些起主要作用的基本块，可以被认为给予那些更重要的基本块更大的权重。
3.3.4 训练、估计、检索
Context-Sensitive Flow Graph and Projective Single Assignment Form for Resolving Context-Dependency of Binary Code
