Lecture 1 -Machine Learning with Graphs.
一.图基础知识
1.节点的度(degree)
设节点的度用$k_i$表示。 无向图 :一条边贡献2个度,故平均度为$ \bar{k}=\langle k\rangle=\frac{1}{N} \sum_{i=1}^{N} k_{i}=\frac{2 E}{N}$
有向图: 度分为入度和出度,因此$\bar{k^{in}} = \bar{k^{out}} = \frac{E}{N}$
2.完全图(complete graph)
每个节点与其他所有节点都有一条边的图。
其边的个数为无向图中最多的边数: \(E_{\max }=\left(\begin{array}{c} N \\ 2 \end{array}\right)=\frac{N(N-1)}{2}\)
属性:
- $E=E_{max}$
- 节点平均度为$N-1$
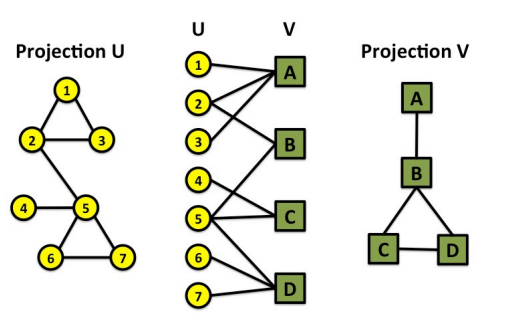
3.二分图(Bipartite Graph)
图中的节点可以被划分到两个独立的子集$U$和$V$,且每条边仅存在于$U$和$V$的节点之间。
折叠网络(Folded Network): 其实可以看成为协作(collaboration)网络。例如,对于集合$U$中的两个节点6,7都存在一条到集合$V$中D节点的边,那么6,7这两个节点被任务有协作关系,因此存在一条边。
4.图的表示
邻接矩阵(Adjacency Matrix)
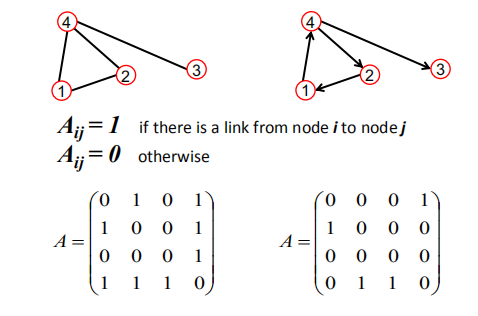
无向图:
- 节点的度为对应行列中非零元素的个数
有向图::
- 节点的入度为列中非零个数,出度为行中非零个数。
存在问题:
- 节点个数多时,矩阵会变得很稀疏
邻接表
用一系列边来表示图。
5.更多类型的图
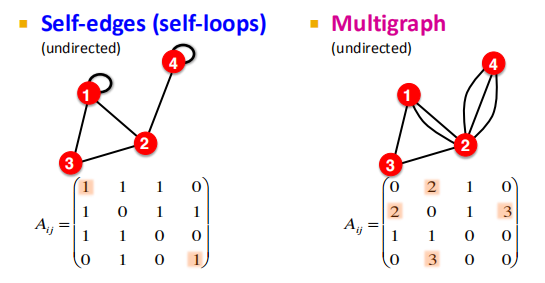
自环图(self-loops): 存在一条自己指向自己的边
多边图(multigraph): 两个节点之间可能存在多条边
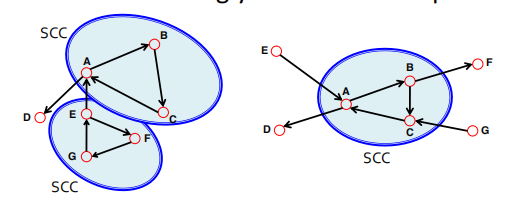
6.有向图的连通性
强连通性: 对每个节点,存在一条到其余节点的路径。
弱连通性: 对于无向图连通,但是对于有向图不连通。
强连通区域(SCCs): 对于图中某一部分的节点是强连通的