Motifs and Structural Roles in Networks
一. Subgraphs, Motifs
1.1 Network Motifs
这里将Network Motifs 定义为:网络连接中重复且重要的模式。这些属性可以帮助我们理解这个网络如何工作和预测网络的功能。
1.导出子图: 导出子图G’,V’∈V,但对于V’中任一顶点,只要在原图G中有对应边,那么就要出现在E’中。
2.重复出现的模式: 如左边这个子图的模式在后面的图中出现了4次。
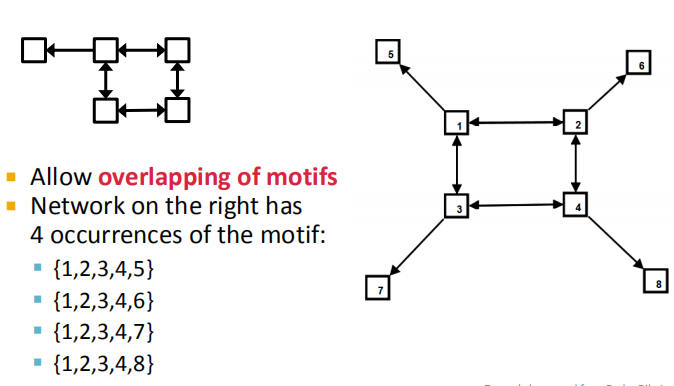
3.重要程度: 在真实网络中子图模式出现的次数,相比于随机网络多,则为OverRepresented;反之,则为UnderRepresented。
形式化定义:
\[Z_i = \frac{N^{real}_i - \bar{N_i}^{rand}}{std(N_i^{rand})}\]其中,$N_i^{real}$为子图i在真实网络中出现的次数,$\bar{N_i}^{rand}$为子图i在随机网络中出现的次数。
归一化之后的网络重要性衡量指标(Significance profile)为:
\[SP_i = \frac{Z_i}{\sqrt{\sum_jZ_j^2}}\]这个分数意味着不同类型的子图的相对重要性分数。
1.2 Configuration Model
上面衡量网络Motifs的一个重要依据是和随机网络做对比,但是我们如何生成满足真实网络度分布的随机网络呢?
第一个模型:
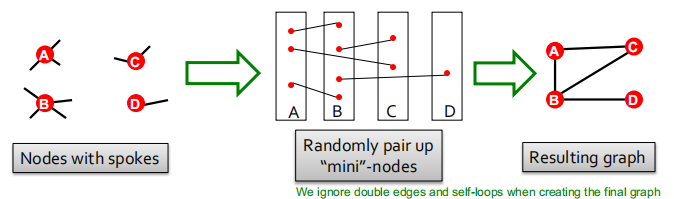
将每个节点打散成小节点,随机配对小节点。但是有个缺点:会有节点间会有双边的情况存在。
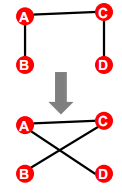
第二个模型: 重复:
- 随机选择一对边$A\rightarrow B,C\rightarrow B$
- 交换这两个边的端点
1.3 Variations on Motifs
针对以上Motifs可以有如下变种:
- 有向和无向
- 有色和无色
- …
二. Graphlets: Node feature vectors
2.1 New Concept: Graphlets
Graphlets: 连通的非同构图
Graphlet Degree Vector(GDV): 这个节点在每个位置上同构子图出现次数的向量。
比如下面这个例子是节点v的GDV:
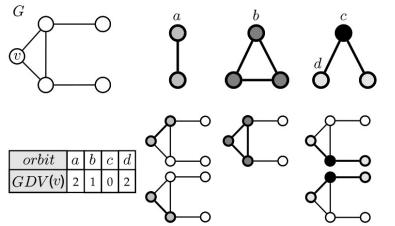
GDV统计了一个节点在特定位置上接触到的graphlets个数,这为我们提供了一种度量节点局部网络拓扑结构的方法。
2.2 Finding Motifs and Graphlets
寻找上面两个部分所描述的motifs和graphlets需要解决如下两个挑战:
- 枚举出所有的连通子图
- 统计每一类子图出现的个数
但是判断一个子图是否出现在另一个图中是个NPC问题。
所以可行的motif size通常很小(3-8)。
2.3 Exact Subgraph Enumeration (ESU)
如今统计子图的算法。
定义了两个集合:
- $V_{subgraph}$:当前构造的子图(motif)
- $V_{extension}$:来扩展motif的候选节点集合
Idea: 从一个节点$v$开始,添加满足如下条件的节点$u$到$V_{extension}$集合中:
- $u$的节点id要大于节点$v$
- $u$为新加入节点的邻居,但不能为早已加入$V_{subgraph}$的节点的邻居

例子如下:当k=3时,可以导出所有节点数为3的子图
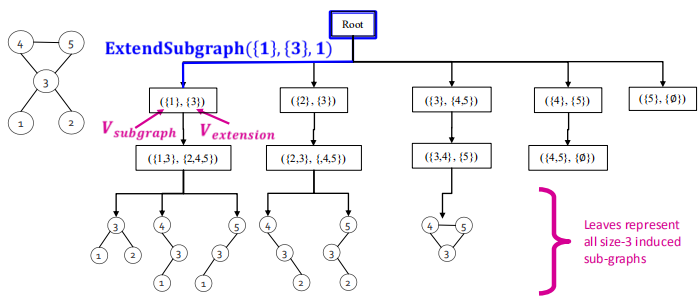
下一步: 统计每类同构子图出现的个数
三.Structural Roles in Networks
Roles: 具有相似结构属性的一群节点
Communities/Groups: 相互连接在一起的一群节点
Structural equivalence: 如果两个节点$u$和$v$对于其他的节点来说具有相同的关系,那么这两个节点为结构等价。
3.1 Discovering Structural Roles in Networks
这里介绍一种名为RoIX的Structural Role发现方法
其工作流程图如下所示:
输入邻接矩阵–>递归的提取特征–>角色提取
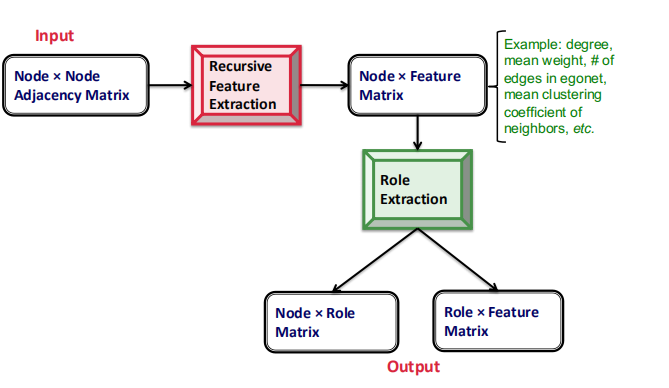
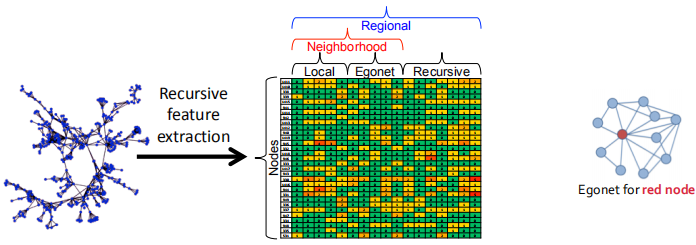
Recursive特征提取: 将网络的连接性转化为结构特征
如下图所示,从网络里为每个节点提取局部特征,然后通过递归的形式生成区域特征。
局部特征: 度、权值
Egonet特征: 节点、邻居和其中的边。比如说在egonet中边的个数、进入或者离开egonet边的个数。
具体流程如下:
- 先从节点特征的基础集合开始
- 使用当前节点特征的集合来生成额外的特征
-
- 两类aggregate函数:mean and sum
-
- 例如求所有邻居节点的度平均值
- 对所有当前的特征进行求和或平均。然后重复
Role提取: 基于提取的特征进行聚类
这种方法可以用来评估节点的结构相似性。