Community Steructure in Networks
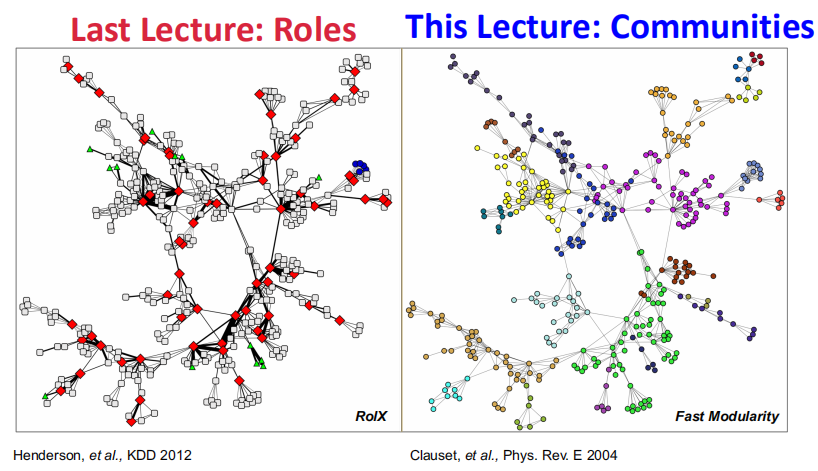
一图胜过万言,上节课研究Structural roles,这节课研究Communities。
一. Granovetter 定理
这个定理其实就是他定义的结论。
Granovetter对于一条边分别在社会和结构上之间的功能做了分析:
首先从结构特征上来看: 在结构上扮演“朋友”的边通常是强社交的;跨不同网络部分的长范围边通常是弱社交的。
其次从信息流动上来看: 长范围的边允许你从不同的部分来收集信息;但在那些扮演“朋友”的边获取信息上通常存在多条冗余路径。
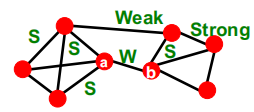
这为之后的社区划分奠定了基础,即同一社区内边更密集且存在冗余,社区之间的边是若相连的。
二.Network Communities
Network Communities定义: 一个集合中的节点具有很多内部相连的边,但是只有很少到外部的边。
首先,需要给出度量一个网络模块化的形式化定义:
Define: Modularity Q: 给定把网络划分到不同不相交的集合$s\in S$的划分

这个公式的作用就是计算每个划分的子集中边的密集程度,如果那么边的密集程度大于期望的(或随机的),那么这个子集就更倾向为一个社区。
Null Model: Configuration Model: 正如刚才提到,需要构建一个随机图来定义一个期望值。
考虑到社区内信息的冗余,构建的图$G’$为multigraph,在保留原有图度分布的情况下,图$G’$中两个节点$i$和$j$之间期望的边数等于:
\[\frac{k_ik_j}{2m}\]因此,对于图$G$的模块化度量由下式所定义:
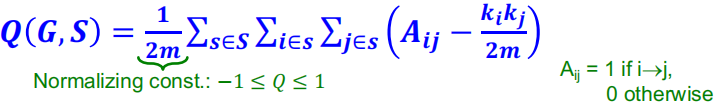
其取值范围是在$[-1,1]$区间中,如果Q的值大于$0.3-0.7$意味着重要的社区结构
三.Louvain Algorithm
这个一个时间复杂度为$O(nlogn)$的社区检测贪心算法,能够提供阶级式(Hierarchical)的社区网络。
效果图如下:
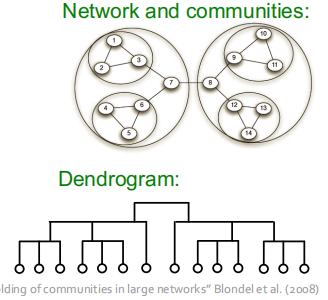
Louvain 算法通过如下两个循环的阶段来最大化modularity:
第一阶段: 通过仅允许节点的局部社区关系变化来最优化modularity。
第二阶段: 合并识别出的社区为一个新的网络。
3.1 第一阶段(Partitioning)
首先划分每个节点为一个不同的社区。
对于每个节点$i$,当将节点$i$加入到一些邻居$j$时,计算出具有最大增量$\Delta Q$的邻居$j$; 然后将节点$i$加入产生最大$\Delta Q$的社区中,重复直至收敛。
这就涉及一个问题,如何定义$\Delta Q$?

上式左边为节点$i$加入社区$C$后的modularity,右边为加入之前的modularity。
但是需要注意的是,上式计算的仅是将节点$i$加入社区$C$时所带来的的增量,我们还需要计算将节点$i$从社区$D$中移出来所带来的增量。所以最后总的$\Delta Q$为:
\[\Delta Q = \Delta Q(i \rightarrow C) + \Delta Q(D \rightarrow i)\]3.2 第二阶段(Restructuring)
只要加入新节点后,社区内仍然是连通的,那么就加进去形成一个大的super-nodes,两个super-nodes之间的权重就为两个社区间所有边权重之和。
之后,阶段一就在这个super-node的网络上继续运行。
四.Detecting Overlapping Communities:BigCLAM
有些节点可能属于多个社区,BigCLAM就是解决这个问题的。
原理没太懂,先省略。。