Spectral Clustering
这一部分来讲述谱聚类算法的产生缘由。
一.Graph Partitioning
首先给出问题:如何做出下图所示的一个分割?
- 最大化组内的连接数
- 最小化组间的连接数
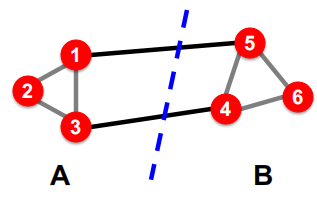
下面我们将这种partition表达为组间”edge cut”的目标函数:
\[cut(A,B)=\sum_{i\in A,j\in B}w_{ij}\]如果是加权图的话$w_{ij}$为权值。
所以我们就最小化上面的目标函数得到组间的最小割,但是这样做存在一个问题:仅考虑了组间的连接,没考虑组内的连接性,因此会出现下图的bad case。
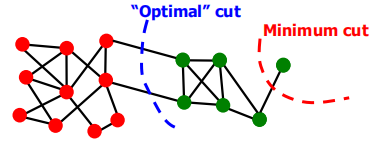
为了考虑组内的连接性,引出了一个概念:Conductance 来平衡组内和组间的重要性,形式化定义如下所示。
\[\phi(A,B) = \frac{cut(A,B)}{min(vol(A),vol(B))}\]其中$vol(A)$为组A内所有节点的度。
二.Spectral Clustering Intuition
这里给定一个邻接矩阵$A$,和每个节点的值向量$\vec x$,我们可以得到
\[A\vec x = \lambda \vec x\]这里我们来分析下$A\vec x$中$j^{th}$坐标上的元素,当为无权图时,$j^{th}$上的值为节点$j$所有邻居值的累加,这就相当于赋予了节点$j$具有邻居属性的新值。
2.1 Spectral Graph Theory
Spectrum: 一个图的特征值$\lambda _i$对应的特征向量$\vec x^{(i)}$,并且特征值是从小到大排序的。
\[\lambda _1 \leq \lambda _2 \leq ... \leq \lambda _n\]如果我们假设图$G$是d-正则且连通的,那么我们可以很容易的得到一个特征值和特征向量:
当$\vec x = (1,1,…,1)$时,有$A\vec x = (d,d,…,d) = \lambda \vec x$,所以特征向量为$\vec x_n=(1,1,…,1)$,特征值$\lambda _n= d$且为最大的特征值。
所以当给定一个连通的d-正则图时,根据上面的发现,我们可以得出额外的结论:$\vec x_{n-1}$的的元素之和必为0。
这是因为,$\vec x_n ^T\vec x_{n-1} = 0$,又因为$\vec x_n=(1,1,…,1)$,所以$\sum_i \vec x_{n-1}[i] = 0$。
这样的话,我们将可以将$\vec x_{n-1}$划分为两类节点:$\vec x_{n-1}[i] >0 $ vs. $\vec x_{n-1}[i]<0$。因此就可以得到两个不同的节点群组。
2.2 Optimization Problem
设节点的邻接矩阵为$A$,度矩阵为$D$,可以得到拉普拉斯矩阵:$L=D-A$。
需要注意的是,生成的拉普拉斯矩阵是半正定矩阵,因此特征值为非负实数,特征向量实数且相互正交。
这里给出一个拉普拉斯矩阵的例子,如下图所示:
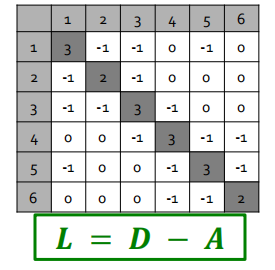
明显可以得出,特征向量$\vec x_1 = (1,1,…,1)$,对应的特征值为$\lambda _1=0$为最小特征值。
这时回顾2.1所讲的Intuition,现在若我们能找到第二小的特征值$\lambda _2$和对应的特征向量,那么我们就可以对将图划分为具有正负标签的两类群组。
根据瑞丽商定理,$\lambda _2$可以这样求得:
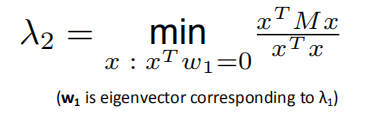
当特征向量为单位向量后,$x^Tx=1$。
那么现在就要探讨下,对于图$G$的$x^T Lx$意味着什么?
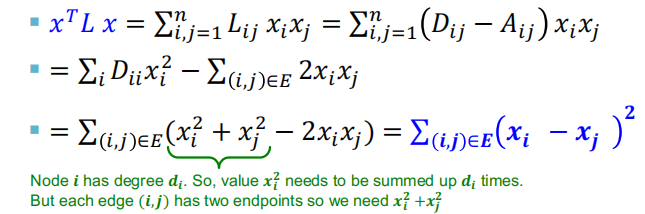
最优化问题的解$x$就为$\lambda _2$的特征向量。
并且我们可以根据$x_2$中值的正负,来将节点分到不同的群组中去。
最后值的注意的是:此优化问题和Conductance的最小化问题是等价的。证明
https://www.cnblogs.com/pinard/p/6221564.html
2.3 谱聚类算法
三个基本阶段:
- 预处理: 构建图的拉普拉斯矩阵表示
- 矩阵分解:求一个或多个最小的特征值和特征向量
- 节点分组:基于节点新的表征,分配节点到多个聚类之中
比如下图,就是根据特征向量$x_2$的正负来进行节点聚类的例子。
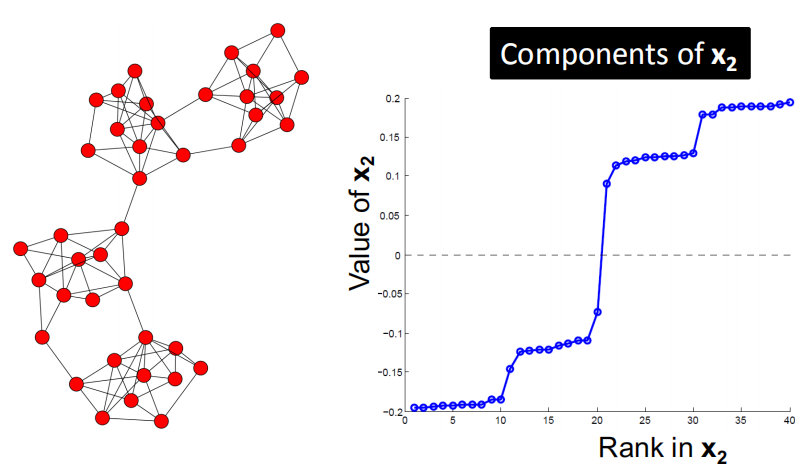
但是为什么只使用$\lambda _2$对应的特征向量呢?难道其他的特征向量都没意义?
当然不是,只是因为$\lambda _2$为第二小的特征值,对于拉普拉斯矩阵来说,特征值越小,特征向量中含有的信息量越大,而第一小的特征值为0,特征向量是没有意义的。所以在实际中,我们可以选择k个最小的特征向量,这样就形成了$n\times k$的特征矩阵,根据每个节点的特征值进行聚类就行了。
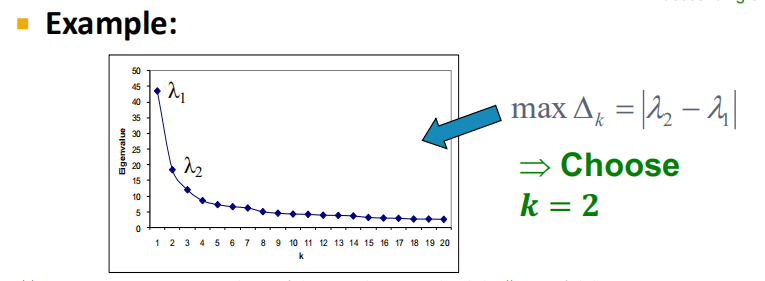
那么应当选什么样的k值比较好呢?
选择具有最大特征值差距的k是最好的:$\Delta k = ||\lambda _k - \lambda{k-1}||$
三. Motif-Based Spectral Clustering
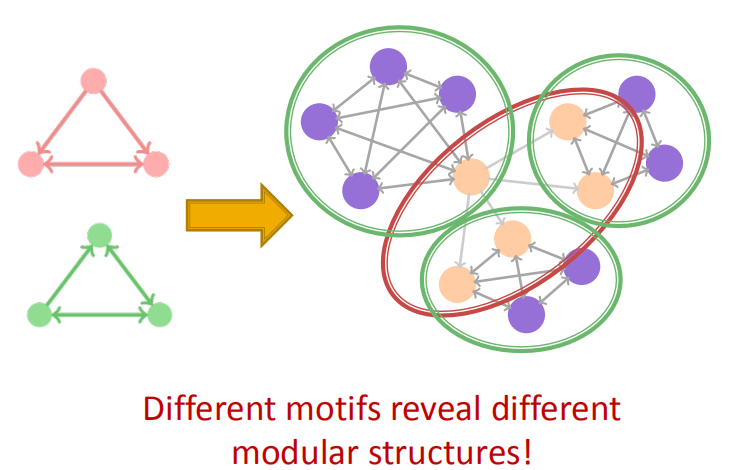
在之前我们是根据边的紧密程度来进行聚类的,那么如果我们想要基于一些其他的模式来进行聚类呢?
研究证明一些小的子图(Motifs)来构成网络中的块。
Motifs概念见https://yunlongs.cn/2020/11/27/cs224w-3/
为了方便理解,给个例子:
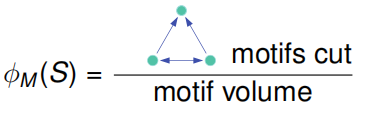
3.1 Defining Motif Conductance
这里我们需要将针对边的目标函数迁移到针对motifs上。

思想:
- 输入:图$G$和motif$M$
- 使用$G$形成一个新的加权图$W^{(M)}$
- 对$W^{(M)}$应用谱聚类
- 输出聚类结果
3.2 Optimizing Motif Conductance
预处理: $W_{ij}^{(M)}= 边(i,j)$出现在motif $M$中的次数
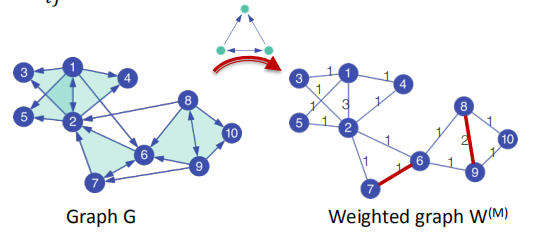
矩阵分解: 基于$W^{(M)}$的标准谱聚类
这样做的Insight在于,对$W^{(M)}$的谱聚类可以帮助找到很低的motif conductance: