Message Passing and Node Classification
这一节课主要讨论的问题是,在一个网络中,只有一些节点具有标签,那么怎么去为所有其他的节点分配标签?
这个问题也可以被称为Collective classification,主要思想是利用网络中已经存在的关系。
对应的三种分类技术分别为:
- Relational Classification
- Iterative classification
- Belief propagation
一.Collective Classification Overview
Markov假设: 节点$i$的标签$Y_i$依赖于它邻居节点$N_i$的标签
\[P(Y_i||i) = P(Y_i||N_i)\]Collective classification涉及三个步骤:
- Local Classifier: 分配初始标签
- 根据节点的特征进行标准分类,但不使用网络信息
- Rleational Classifier:捕捉节点之间的关系
- 基于邻居节点的标签或特征学习出一个节点分类器,使用了网络信息
- Collective Inference: 通过网络传递关系
- 迭代的对每个节点应用Relational classifier,最后网络结构将会影响到节点的预测结果
二.Relational Classifier
基本思想: $Y_i$的分类概率为它邻居分类概率的加权平均
\[P(Y_i=c) = \frac{1}{\sum_{(i,j)\in E} W(i,j)} \sum_{(i,j) \in E} W(i,j)P(Y_j = c)\]- 对于有标签的节点,我们初始化为它们本身的标签$Y$。
- 对于没有标签的节点,均匀地初始化$Y$
- 以随机的顺序来更新所有的节点,直到收敛或者达到迭代的最大数
Challenge:
- 不保证收敛
- 此模型没有使用节点的特征信息
三.Iterative Classification
正如前面所说,Relational Clssifier并没有利用到节点属性的信息,那么我们应当如何利用它们呢?
Iterative classification的主要思想: 基于节点$i$自身的特征和其邻居节点集合$N_i$的标签来进行分类
我们可以总结下要做的流程:
- 首先为每个节点创造一个特征向量$a_i$
- 然后使用特征向量$a_i$来训练一个分类器
- 对于节点的邻居,我们可以使用将它们的信息进行累积:count, mode, proportion, mean, exists…
3.1 具体流程
BootStrp 阶段:
- 为每个节点分配一个特征向量$a_i$
- 根据特征向量,使用分类器$f(a_i)$ (e.g.,SVM,KNN) 来为节点$i$计算最佳的标签$Y_i$
Iteration 阶段: 对于每个节点$i$,重复地更新节点特征向量$a_i$,然后根据$f(a_i)$来更新节点标签$Y_i$
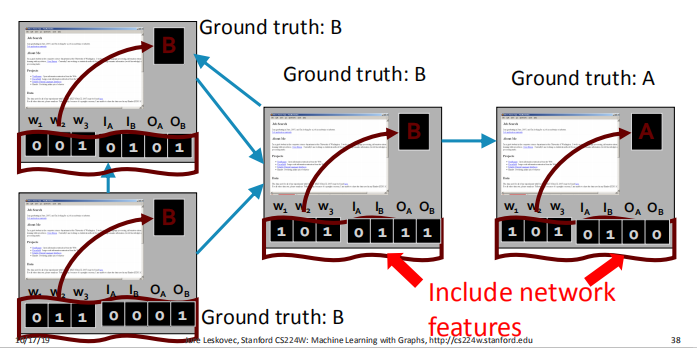
3.2 Example:Web Page classification
对每个节点(网页)分配一个特征向量,这个特征向量由两部分组成:
- 第一部分就为该节点中关键词的个数
- 第二部分为一个表示邻居节点标签的向量$(I_A,I_B,O_A,O_B)$。其中$I=In,O=Out$,例如,$I_A=1$就代表着至少有一个指向此节点的邻居节点标记为$A$。
四.Loopy Belief Propagation
4.1 Notation
Label-label potential matrix $\psi$: 来表征节点和其邻居节点之间的依赖关系。$\psi (Y_i,Y_j)$为在给定具有状态为$Y_i$的邻居节点$i$的情况下,节点$j$为状态$Y_j$的概率。
Prior belief $\phi$: 节点$i$为状态$Y_i$的概率$\phi_i(Y_i)$
$m_{i \rightarrow j}(Y_j)$ 为当$j$为状态$Y_j$时,节点$i$传递给$j$的消息
$\mathcal{L}$ 为所有状态的集合
4.2 算法流程
首先,初始化所有的消息为1,然后为每个节点重复的计算传递的消息:
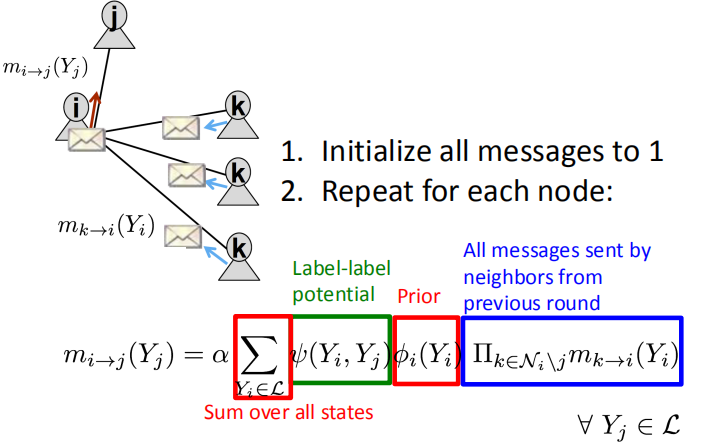
当收敛之后,$b_i(Y_i)$就为节点$i$在状态$Y_i$下的belief,其形式化如下:
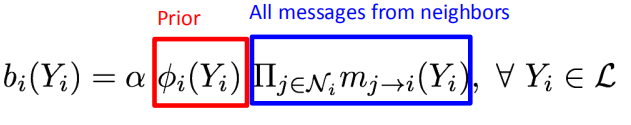
至于其中的参数,通常由基于梯度的优化算法来进行学习。
Notice: 当图中存在回路的时候,Belief Propagation可能会出错,但是通常在实际使用的过程中,因为边之间的弱连接和长回路,造成的影响通常很弱。