Graph Representation Learning
图表征学习减轻了之前ML的从业人员手工提取特征的负担,重要性不言而喻。
一. Embedding Nodes
Node embedding 的目标就是对节点进行编码,并且在embedding space的相似性约等于在原始网络中的相似性。
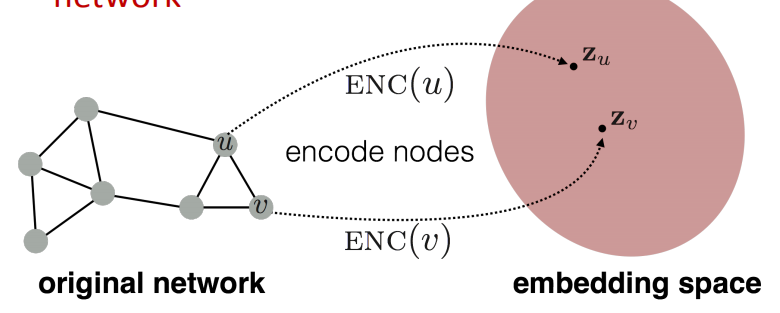
所以这就需要我们:
- 定义一个encoder 来映射节点为embedding
- 定义一个节点相似性函数 来衡量在原来网络中的相似性
- 优化encoder的参数 来使得在原来网络中的相似性,约等于embedding空间中的相似性。
下面就介绍三种node embedding的算法
1. DeepWalk
这个我以前介绍过,就不再介绍。链接:https://yunlongs.cn/2019/04/26/NE-Deepwalk/
2. Node2vec
这个我以前也介绍过,不再介绍。连接:https://yunlongs.cn/2019/04/26/NE-Node2vec/
3. TransE-Translating Embedding for Modeling Multi-relational Data
TransE 将图看作为具有知识的图(知识图谱),其中的节点为实体,边为关系,但是图中的边具有不同的为种类,正如你和不同人具有不同的关系一样。
在TransE中,实体之间的关系被表达为一组triplets: \(h(head entity),l(relation),t(tail entity) \rArr (h,l,t)\)
首先,类似于之前的方法,先将实体嵌入到实体空间$R^{k}$中,并且可以将实体之间的关系表达为translations:
- 如果给定的关系是对的,那么$h + l \approx t$
- 否则,$h+l \neq t$
因此,对于TransE来说,其要做的事就是区分这些真关系和假关系:

所以,TransE的整个算法流程如图所示:

二. Embedding Entire Graphs
方法1: Simple idea:在图上运行标准的图嵌入算法,来得到节点的embeddings,然后直接对节点的embedding进行求和或者平均:
\[Z_G=\sum _{v\in G}z_v\]方法2:
Idea:引入一个“虚拟节点”来表示一个图,然后进行图嵌入技术
方法3:Anonymous Walk Embeddings
匿名随机游走中,遍历到的每个节点的状态为在此随机游走中第一次遇到此节点的索引。
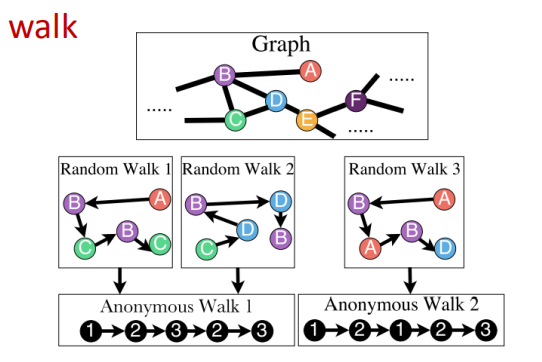
但是,随着游走长度的增长,可能的不同匿名随机游走个数会指数增长。比如当游走步长为3时,有5条可能的游走路径:$a_1=111,a_2=112,a_3=121,a_4=122,a_5=123$
步骤1:统计所有步长为$l$的匿名游走$a_i$出现的次数,然后对这些随机游走进行概率建模
例子:当$l=3$时,我们有5条可能的匿名游走,我们建模每类游走为$Z_G[i]=$在$G$中匿名游走$a_i$出现的概率
步骤2:对匿名随机游走进行采样,但因为完全统计完所有的匿名游走是不现实的,所以我们可以生成一个具有m条随机游走的集合,并计算其对应的经验分布。

步骤3:学习walk embedding。这里我们需要为每一个匿名游走$a_i$学医一个embedding $z_i$,而图$G$的embedding 为walk embedding $z_i$ 的累积操作。
但是我们如何embed walk呢?Idea: 预测游走的下一步。
给一个匿名游走序列$z_i$,我们来最大化
\[P(W_t^u \| W_{t - \delta}^u,...,W_t^u) = f(z)\]其中$w_t^u$为从$u$节点出发的随机游走的第t步。
之后,我们从$u$节点开始进行$T$个不同的随机游走,得到$N_R(u) = \lbrace w_1^u,w_2^u,…,w_T^u \rbrace$
