Graph Neural Network
上一讲的内容,描述了几个经典的图嵌入算法,将节点映射到低维的向量中,并且在embedding空间仍然具有原来空间的相似性。
这一讲中,我们将会讨论基于图神经网络的深度学习方法。
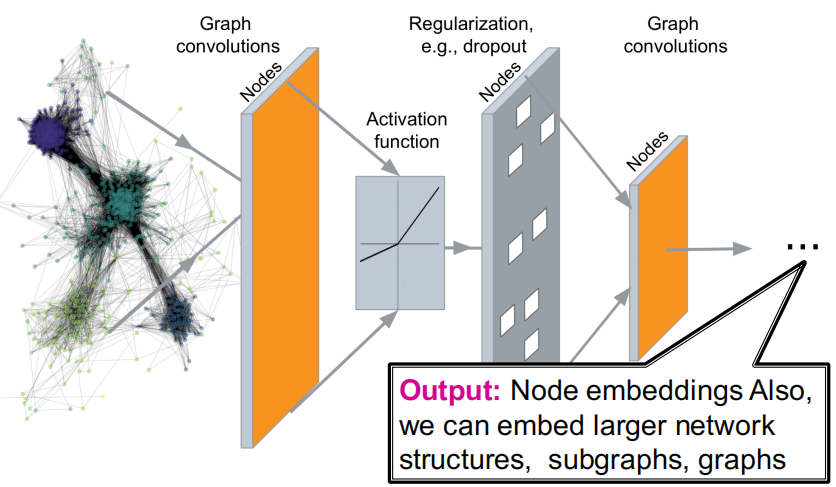
一.图神经网络的困难
目前深度学习中较为成功的两大领域:CV和NLP,CV以图像作为处理对象,而图像可以轻松的用像素矩阵来表示;NLP处理文本信息,而文本信息都是以序列形式存在。
但是对于图来说,如下的复杂性导致图神经网络研究的困难性:
- 可以是任意的大小和复杂的拓扑结构
- 节点次序不固定
- 通常图是动态变化的切具有多模态的特征
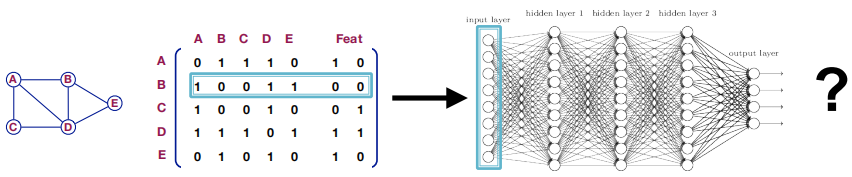
如果我们直接将网络的邻接矩阵和节点特征输入到神经网络中,我们会有如下的问题:
- 参数的个数和随着节点个数的增加,急剧增加
- 不适应与不同大小的图
- 会受到节点之间次序的影响
但是,我们仍可以从CNN中借鉴些有用的模式: 如下图所示,$3 \times 3$的卷积的作用是提取一个像素及其邻居的特征作为一个新的像素点,而应用在图中,将节点邻居和自身的信息融合为一个新的message正是一个不错的想法。

二.Graph Convolutional Networks
2.1 Setup
给定一个图$G$,我们设置:
- $V$为节点的集合
- $A$为邻接矩阵(假设为二元的)
- $X \in \reals ^{m \times |V|}$ 为节点特征矩阵
2.2 Basic idea of GCN
回忆下上一讲的Belief Propagation,可以将局部的信息传递到自身,那么我们是不是可以将节点及其邻居这个局部网络定义为一个计算图,用来学习如何在图上传递信息来计算节点的特征?
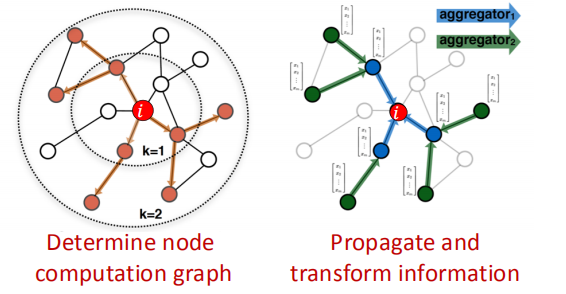
由此就可以引出我们GCN的原型: 我们基于节点的局部网络邻居来生成节点的embeddings,而从邻居收集的消息则使用神经网络来进行累积计算。
因此,模型可以使任意的深度,这意味着:
- 在每一层节点都会有个embedding
- 在第0层节点的embedding则为其输入特征
- 第k层的embedding则从k-跳的邻居中获得了信息

2.3 GCN Neighborhood Aggregation
最关键的一步,就是如何定义这个神经网络来累积邻居信息?
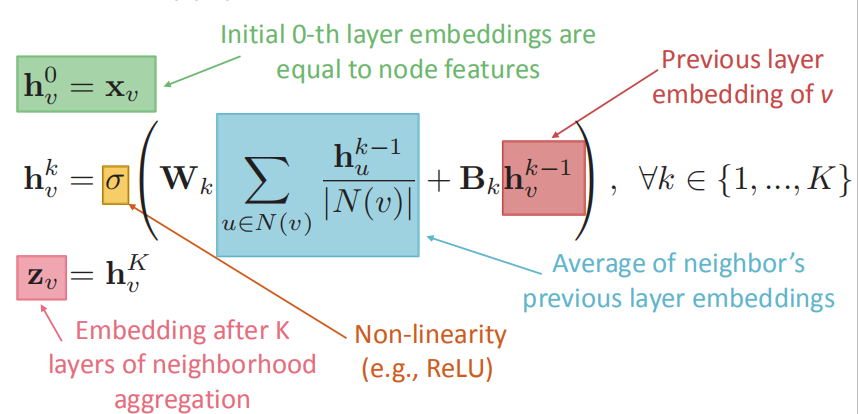
下图中的公式定义了神经网络如何来处理、累积邻居信息及融合自身特征进行消息传递:
- $W_k和B_k$都为要训练的参数,作为体现为分别对邻居信息和自身特征作变换,来决定邻居信息的重要程度和自身特征的重要程度
- $\sigma$函数为非线性函数
- 蓝色部分为对邻居的前一层embeddings进行求平均
- 红色部分为前一层自身节点的embedding
上面的公式可以向量化为:
\[H^{l +1 } = \sigma (H^{(l)}W_0^{(l)} + \tilde{\mathbf{A}} \mathbf{H}^{(l)} \mathbf{W}_{1}^{(l)})\]其中,$\tilde A = D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$,$H^{(l)} = [h_1^{(l)^T},…,h_N^{(l)^T}]$
因此,最后输出的节点embedding将同时兼具自身的特征和邻居信息以及网络拓扑结构丰富的信息。
2.4 How to Train the Model
在得到了节点的embedding后,我们可以定义任意的损失函数并使用随机梯度下降来训练模型的权重参数。
你可以使用无监督的形式来训练,就像上一讲将的DeepWalk算法一样,来将相似的节点学习到相似的embedding中。
也可以用监督学习的形式来训练,比如节点分类。
2.5 Inductive Capability
当模型训练好之后, 对于所有的节点来说我们一组共享参数,因此对于unsee的节点,我们也能进行很好的预测,如下图所示。

值得注意的是,图神经网络的深度有两种不同的类别:
- 第一类为游走序列的深度,这决定了你想捕捉信息的范围,以及你的图神经网络会有几层,如上图下半部分。
根据我们在第二讲中对MSN巨大的网络进行分析,其网络直径为6,也就是说只需最多6跳,MSN网络中任意节点的消息将会传递到自己。
- 第二类为神经网络cell中网络深度,每个cell中神经网络的深度决定了学习的非线性程度。
三.GraphSAGE
在刚才将的GCN模型中,对邻居消息的累积函数是固定的(average),有什么更好的方式吗?
GraphSAGE对Neighborhood Aggregation函数进行了改进:
\[\mathbf{h}_{v}^{k}=\sigma\left(\left[\mathbf{W}_{k} \cdot \operatorname{AGG}\left(\left\{\mathbf{h}_{u}^{k-1}, \forall u \in N(v)\right\}\right), \mathbf{B}_{k} \mathbf{h}_{v}^{k-1}\right]\right)\]即:1.将之前的邻居向量和自身特征向量的求和。2.取代平均函数为一个通用累积函数
而这个累积函数可以为:
- Mean \(\mathrm{AGG}=\sum_{u \in N(v)} \frac{\mathbf{h}_{u}^{k-1}}{|N(v)|}\)
-
Pool:对邻居向量进行变换,然后应用max/mean函数。其中$Q$为变换矩阵,$\gamma $为pool函数 \(\mathrm{AGG}=\underline{\gamma}\left(\left\{\mathbf{Q} \mathbf{h}_{u}^{k-1}, \forall u \in N(v)\right\}\right)\)
- LSTM:直接对邻居向量应用LSTM,但是邻居节点的顺序需要打乱,然后学习多次 \(\mathrm{AGG}=\mathrm{LSTM}\left(\left[\mathbf{h}_{u}^{k-1}, \forall u \in \pi(N(v))\right]\right)\)
四.Graph Attention Networks(GAT)
在之前讲的内容,一直在假设每个邻居的贡献都是一样的,但是事实上,这并不成立。
GAT定义了$\alpha_{vu}=1/|N(v)|$为节点$u$的消息传递给节点$v$的权重因子,其为注意力机制$\alpha$计算出的一个副产品:
-
基于节点对$u,v$的消息来计算出注意力系数$e_{vu}$,其暗示了节点$u$的消息对于节点$v$的重要性 \(e_{vu} = \alpha (W_k h_u^{k-1},W_k h_v^{k-1})\)
-
标准化系数使用softmax函数来比较不同邻居间消息的重要性: \(\alpha_{v u}=\frac{\exp \left(e_{v u}\right)}{\sum_{k \in N(v)} \exp \left(e_{v k}\right)}\) \(\boldsymbol{h}_{v}^{k}=\sigma\left(\sum_{u \in N(v)} \alpha_{v u} \boldsymbol{W}_{k} \boldsymbol{h}_{u}^{k-1}\right)\)
但是,注意力机制$\alpha$的形式是什么样的呢?
- 可以选择$\alpha$为方法无关的选择:可以具有要学习的参数,可以使用简单的神经网络
- 可以和图神经网络的其他权重参数一起训练
另外,提一下GAT的升级版: Multi-head attention: 可以稳定注意力机制的训练过程
- 对给定的layer进行独立的attention操作,重复R次,每次用不同的注意力参数
- 对每个head的输出结果进行累积
这不和Transformer一毛一样🐴