Deep Generative Models for Graphs
温馨提示:Lecture 9是编程课,所以就不写笔记了哈
如这一讲的标题所示,来研究图的生成模型。
一.图生成模型的难点所在
- 非常大的变量输出空间
如果要生成具有n个节点的图,那么其邻接矩阵中就有$n^2$条边的参数要进行学习。
- 图不唯一的表征
n个节点的图通过节点顺序的置换,可以表征成$n!$个不同的邻接矩阵
- 节点间复杂的依赖关系
节点间长范围的依赖关系很难不活,有些边的存在甚至于依赖于整个图。
二.Recap:Generative Models
Given: 从$p_{data}(G)$中采样的图样本
Goal: 从数据中学习出分布$p_{model}(G)$,然后从中采样。

(1)首先要使$p_{model}(x;\theta)$与真实的数据分布$p_{data}(x)$分布足够接近
关键原理是:极大似然,寻找出能最佳拟合训练数据的参数$\theta$
\[\boldsymbol{\theta}^{*}=\underset{\boldsymbol{\theta}}{\arg \max } \mathbb{E}_{x \sim p_{\text {data }}} \log p_{\text {model }}(\boldsymbol{x} \mid \boldsymbol{\theta})\](2)从训练好的$p_{model}(x;\theta)$中进行采样
图生成模型使用自回归的模型来进行采样,比如说RNN。$p_{model}(x;\theta)$既用来进行参数估计,也用来采样。
这种方式需要应用链式规则:即每个时间步都依赖于之前的状态
\[p_{\text {model}}(\boldsymbol{x} ; \theta)=\prod_{t=1}^{n} p_{\text {model}}\left(x_{t} \mid x_{1}, \ldots, x_{t-1} ; \theta\right)\]而在我们的例子中:$x_t$将代表的是第t个时间的动作(添加节点,添加边)
三.GraphRNN: Generating Realistic Graphs
3.1 Model Graphs as Sequences
GraphRNN的主要思想就是,把图生成的过程当成为添加节点、添加边的序列生成过程。
这里我们给定一个图的节点次序$\pi$,并从1-5标号,我们将图序列建模为:
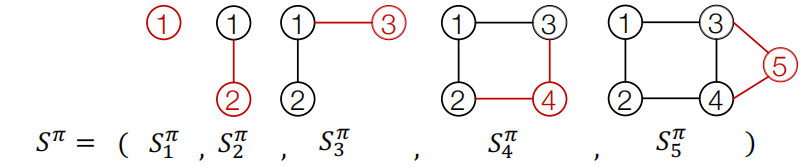
图序列$S^\pi$的生成包含两个级别的任务:
- 节点级别: 每个时间步添加一个节点
- 边级别: 每添加一个节点时,就添加此节点与已存在节点之间的边
节点级别的生成任务就不细讲,就是根据节点序列$\pi$,每个时间步添加下一个节点。
边级别的任务,以节点4为例子,在上图中,添加节点4时,图中已存在节点1-3,因此在第4个时间步要考虑节点4与这些节点的连通性。

总结: 一个图+一个节点次序就可以得到一个图序列。
而当节点次序确定的时候,图的邻接矩阵就非常完美的可以展示这个图序列:如下图所示,当给定第一个节点的时候,邻接矩阵的每一行就代表每个时间步节点级别的序列生成任务,而邻接矩阵的每一列就代表在当前时间步下边级别的序列生成任务。
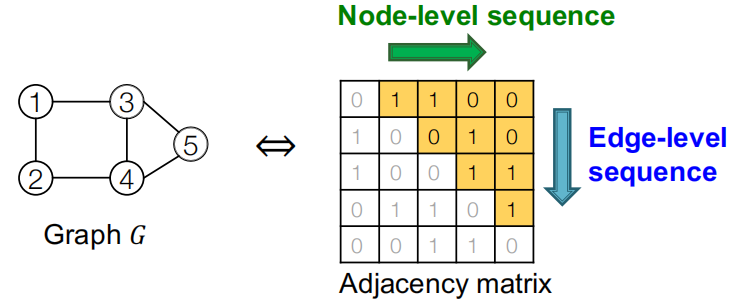
有了图序列,我们自然可以想到用RNN来进行序列生成!
3.2 GraphRNN: Two Levels of RNN
刚才提到了,我们需要进行节点级别和边级别的序列生成任务,那么就我们就结合上面的邻接矩阵来看下图:
同样,横着的每个RNN cell每个时间步添加一个新的节点,并把当前的图状态传递给下一个时间步;竖着的每个RNN Cell在当前时间步来预测与之前每个节点存在边的概率。
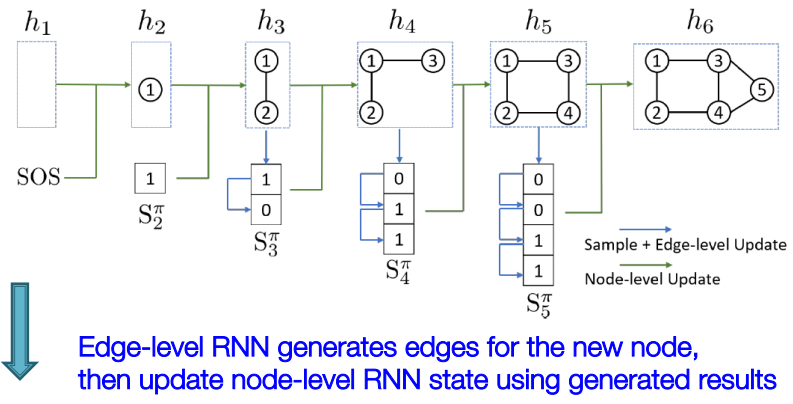
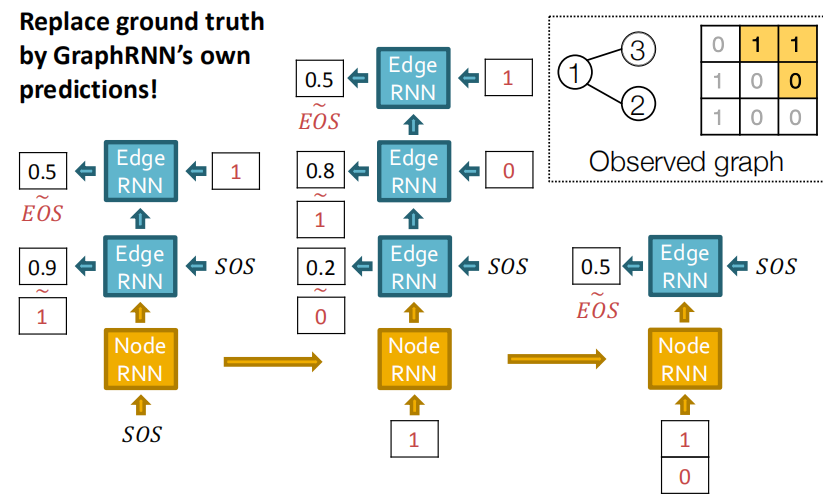
训练过程: 如下图所示,图的第一个节点不用生成,当给定第一个节点时,添加节点2并使用SOS来初始化Node RNN,此时Edge RNN来决定节点2和节点1之间有没有边,并把这条边的ground truth传递给下一个Edge RNN,此时节点2添加完毕。
然后添加节点3并使用上一个Node RNN的状态当做输入,并使用Edge RNN来决定节点3与节点1、2之间有没有边。
当遇到终结Node RNN时,则代表图生成完毕。
损失函数可以使用二分类交叉熵来进行训练。
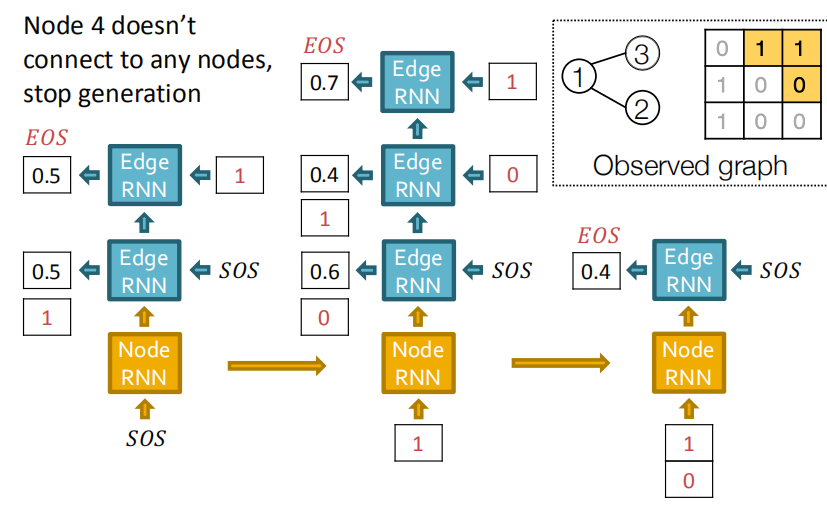
测试过程: 基本和RNN的序列生成过程一样,把Edge RNN的输出当为下个Edge RNN的输入。
3.3 Issue:Tractability
在进行图生成的过程中,我们应当注意到,当进行越来越多的时间步时,当前节点与之前节点要考虑的边依赖就越来越多,所以当添加第1000个节点时就要考虑和之前999个节点的依赖关系,这样的依赖关系太过于复杂。。
解决方案: 从初始节点开始,使用BFS来对节点进行排序。
如下图所示,节点4并不连接节点1,而此时节点1的邻居早已遍历添加过了,因此之后添加的节点5就不再需要考虑和节点1之间的关系。这样我们仅需要记忆很少的步数就可以了。
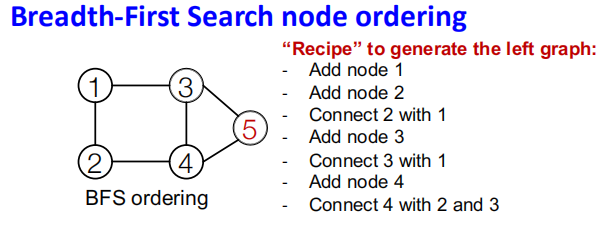
BFS的节点序带来的好处也是显而易见的,降低了边生成所需要的步数,每个节点只需要考虑局部的邻接信息就行。
