Reasoning over Knowledge Graphs
第11-16讲的内容,不是我所重点关注的,就不花费时间写了。
一.Knowledge Graph completion
在FreeBase的数据集上,研究人员发现93.8%的人没有填写出生地,78.5%的人没有填写国籍信息。
那么,给定一个非常大的知识图谱,我们如何来补全知识图谱中丢失的关系呢?
1.1 KG Representation
我们将在KG中的边表达成一个三元组(h,r,t) :头结点h,关系r,尾节点t。
主要思想:
- 将KG中的实体和关系建模到同一个向量空间$\Reals ^d$
- 给定一个正确的三元组(h,r,t),我们的目标为对于(h,r)的embedding,应当和t的embedding足够接近。
所以之后要讨论的就是如何嵌入实体和关系,如何定义距离。
1.2 Relation Patterns
这里我们形式化下KG中常见的几种关系。
- Symmetric Relations:
例如:家庭关系、室友关系
- Composition Relations:
例如:我的妈妈的丈夫为我的父亲
- 1-to-N,N-to-1 Relations:
例如:h为老师,t为学生,r为师生关系
1.3 TransE
对于一个三元组(h,r,t),我们将h,r和t均映射到d维的实数空间中,并且还要想令
\[h + r =t\]这里我们设定Socure function: $f_r(h,t) = |h + r-t|$
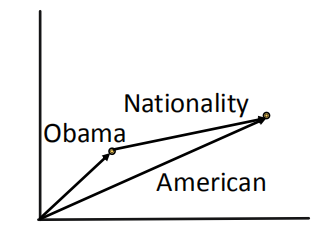
如下图所示,我们将实体”Obama”、”American”和关系”Nationality”映射到向量空间中,并且希望在向量空间中实体”Obama” + “Nationality” 的向量尽可能接近 “American”的向量。
为了训练参数,能够使KG中的实体和关系嵌入到有意义的向量,我们使用Triplet Loss来训练:
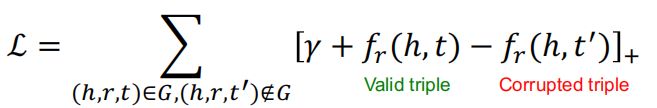
这里使用TransE来进行KG中的链接预测:

TransE的局限性:Symmetric Relations 我们期望
\[r(h,t)\rArr r(t,h) \ \ \ \ \ \ \ \ \forall h,t\]即$|h+r-t| =0$和$|t+r-h|=0$,但这样做的话,将会出现$r=0,h=t$的情况,但是h和t是不同的实体,应当映射到不同的向量中。
TransE的局限性:N-ary Relations 我们期望$(h,r,t_1)$和$(h,r,t_2)$在KG中成立,但是$t_1 = h+r = t_2$,对于相同的h和r得到的t总是相同的,但他们应当是向量空间中不同的两个实体。
1.4 TransR
TransR将实体建模到实体空间$\Reals ^d$的向量中,将关系建模到关系空间$\Reals ^k$的向量中去,然后使用一个投影矩阵$M_r \in \Reals ^{k \times d}$来将实体从实体空间映射到关系空间中去。
这里,给定实体空间的两个实体$h,t$,其投影到关系空间后为:
\[h_{\perp}=M_{r} h, t_{\perp}=M_{r} t\]相应的,对这个三元组的评分函数变为:
\[f_r(h,t) = \|h_ \perp + r - t_ \perp \|\]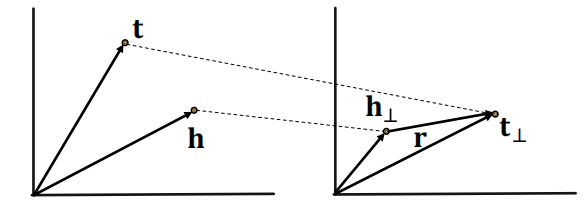
相比于TransE,TransR可以容易的处理Symmetric Relations:
\[r(h,t)\rArr r(t,h) \ \ \ \ \ \ \ \ \forall h,t\]这是因为,h和t可以映射到关系空间中相同的节点上。
\[r=0,\ h_ \perp = M_rh = M_rt = t_ \perp\]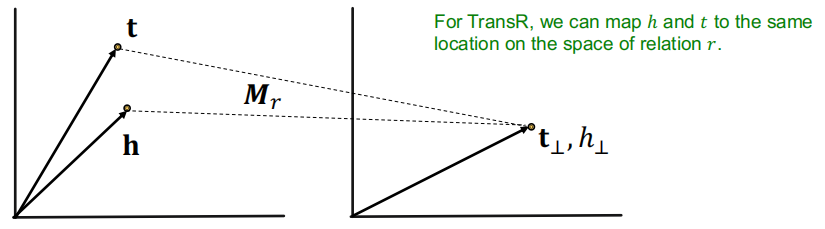
TransR可以容易的处理N元关系:
给定KG中中的$(h,r,t_1)$和$(h,r,t_2)$,我们可以将$t_1,t_2$映射到关系空间的同一个点上去,就有
\[t_ \perp = M_rt_1 = M_rt_2\]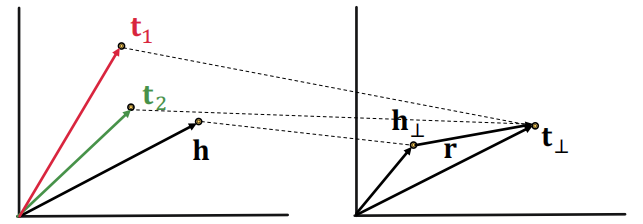
但TransR同样就有局限性: 不同建模 Composition Relations
\[r_1(x,y) \land r_2(y,z)\rArr r_3(x,z) \ \ \ \ \ \forall x,y,z\]这是因为一个很自然的事实,关系并不是说是由多个关系组合而成。
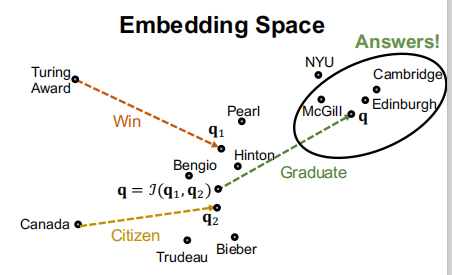
二.Path Queries
我们可以将一个查询,转化为一个查询路径,并在路径上不断的添加更多的关系。
比如,路径查询可以表达为:
\[q = (v_a,r_1,...,r_n)\]从一个起点出发,然后添加各种关系,来找到想要的答案。
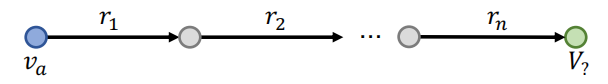
比如,问题: “Where did Turing Award winnners graduate?” ,其中初始节点为”Turing Award”,要添加的关系为”win”、”graduate”。
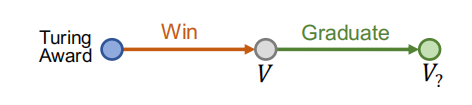
在每此路径上的每一步,我们根据对应的关系找到相关的节点,然后完成对所有关系的查询,就可以找到符合所有关系的答案。
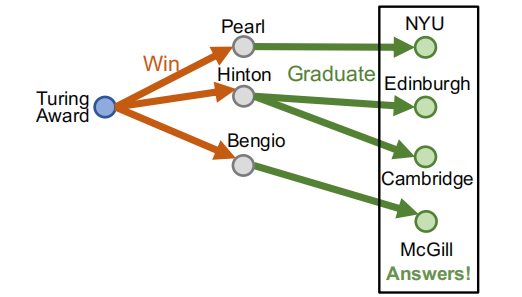
但是,有个问题,当图中很多关系缺失的时候,怎么办?
如果我们先预测图中的链接,进行补全,再进行路径查询的话,那么开销就太大了。因为对于每种关系,都需要对图中的节点进行两两预测。
关键思想: 将查询(即关系)进行嵌入,其实就是将TransE泛化到一个多跳的任务中去
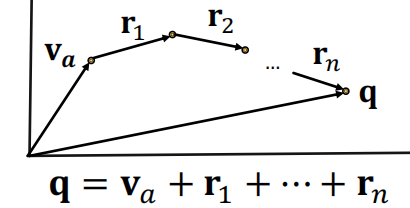
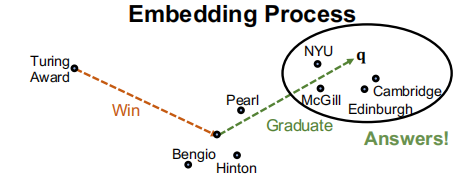
三.Conjunctive Queries
我们要构建一些复杂的联合查询,比如
“Where did Canadian citizens with Turing Award graduate?”
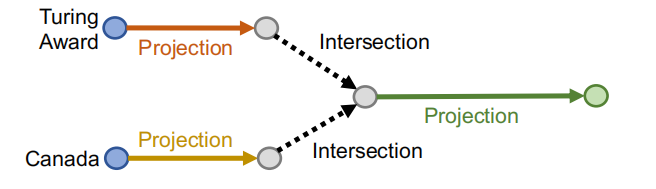
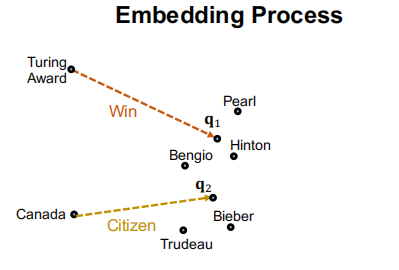
那么我们如何定义在向量空间的这个交集呢?
定义了个神经网络交集操作$J$:
- 输入当前的查询向量$q_1,…,q_m$
- 输出:查询向量q的交集
- $J$应当是置换不变的,因为查询的关系先后顺序和结果无关。即 \(\mathcal{J}\left(\mathbf{q}_{1}, \ldots, \mathbf{q}_{m}\right)=\mathcal{J}\left(\mathbf{q}_{p(1)}, \ldots, \mathbf{q}_{p(m)}\right)\)
所以,整个网络,即DeepSets的架构如图所示:
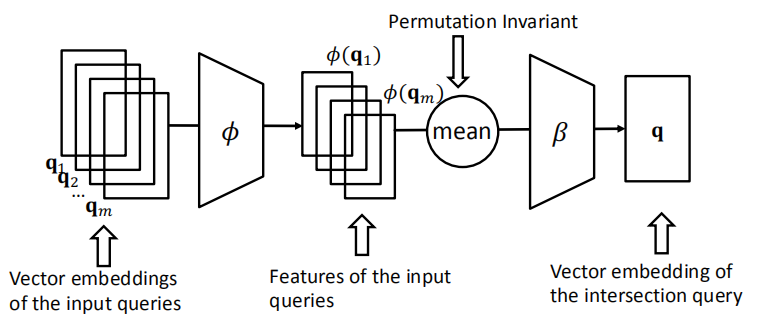
得到交集之后,再进行下一跳的查询即可: