网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes2.pdf
Lecture 5 -Gaussian Discriminant Analysis. Naive Bayes.
生成学习算法（Generative Learning Algorithms）
之前学习的分类和回归算法中，都是试图去直接学习$p(y|x)$或者输入X的空间映射到标签{0，1}，这些算法称作为判别学习算法(discrimative learning algorithm) 。 在接下来，将会介绍试图对$p(x|y)$ (and $p(y)$)进行建模的算法 ，这类算法称作为生成学习算法(generative learning algorithms) 。 例如，$p(x|y=0)$ 是对乳腺癌良性肿瘤的特征建模，$p(x|y = 1)$是对乳腺癌恶性肿瘤的特征建模。
当我们使用GLA对问题建模获得p(y)和p(x|y)后，我们可以利用贝叶斯公式来导出p(y|x)：
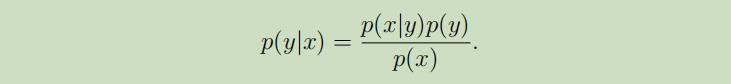$p(x) = p(x|y = 1)p(y = 1) + p(x|y =0)p(y = 0)$
然而，实际上， 在计算p(y|x)来进行预测时，我们并不需要计算$p(x)$：
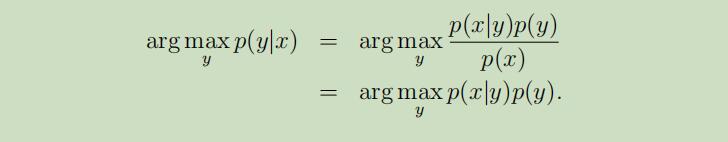
多元高斯模型
多元高斯模型的参数有期望$\mu \in \mathbb{R}^{n}$，和协方差$\Sigma \in \mathbb{R}^{n \times n}$。其中$\Sigma \geq 0$是半正定矩阵。其可以写为：“$\mathcal{N}(\mu, \Sigma)$”，其概率密度函数为：
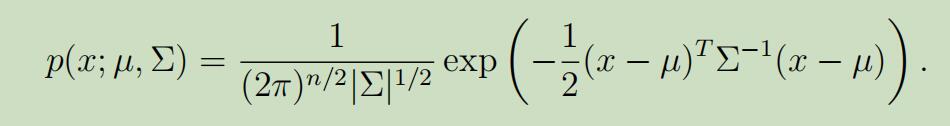
对于多元高斯模型给定随机变量$X$时，它的期望为：
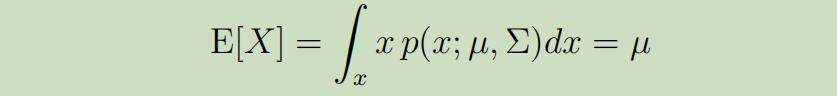
现在让我们泛化概率论中关于协方差的两个公式：
- $Cov(Z)=\mathrm{E}\left[(Z-\mathrm{E}[Z])(Z-\mathrm{E}[Z])^{T}\right]$
- $Cov(Z)=\mathrm{E}\left[Z Z^{T}\right]-(\mathrm{E}[Z])(\mathrm{E}[Z])^{T}$
所以当$X \sim \mathcal{N}(\mu, \Sigma)$时，可以得到：
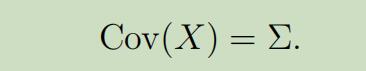
为了能够更加清晰的了解多元高斯分布，现在我们看下它的概率密度图像：
上面最左边的图为多元标准正态分布的图像，是在只有两个特征的情况下，它的期望为$2 \times 1$的零向量，协方差为 $2\times 2$的单位矩阵；中间图的分布的期望为零向量，协方差$\Sigma=0.6 I$；最右边图的分布，期望为零向量，协方差$\Sigma=2 I$。
可以看出来，协方差越大，图像越“扁平”；协方差越小，图像越“尖锐”
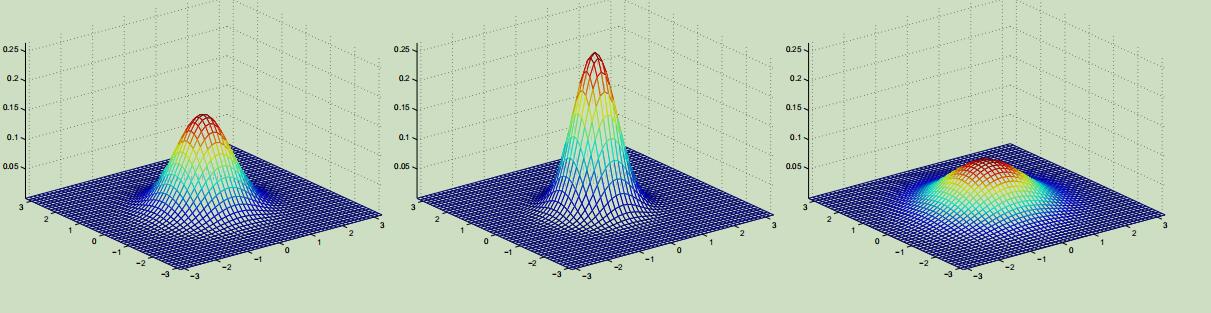
同样，这些例子的期望也都还是零向量，但是它们的协方差分别为：
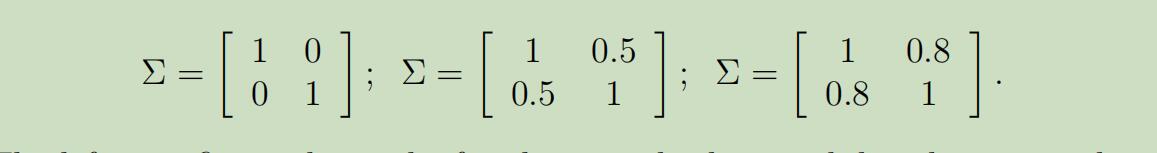上图最左边的为标准正态分布，可以看出来随着协方差矩阵副对角线的值越来越大，在45°的方向上（即x1=x2），图像越来越像是在这个方向上被“压缩”了一般。
我们将上面的这些分布投影到二位平面上可以得到如下的图样：
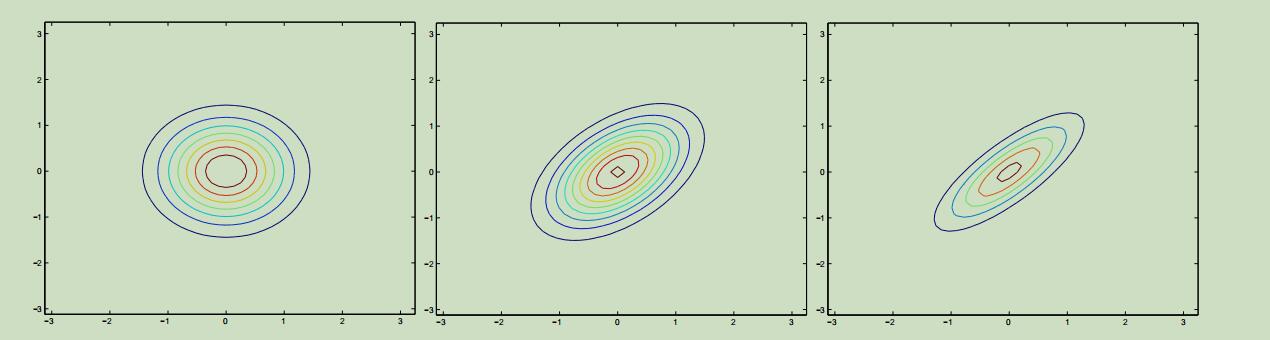
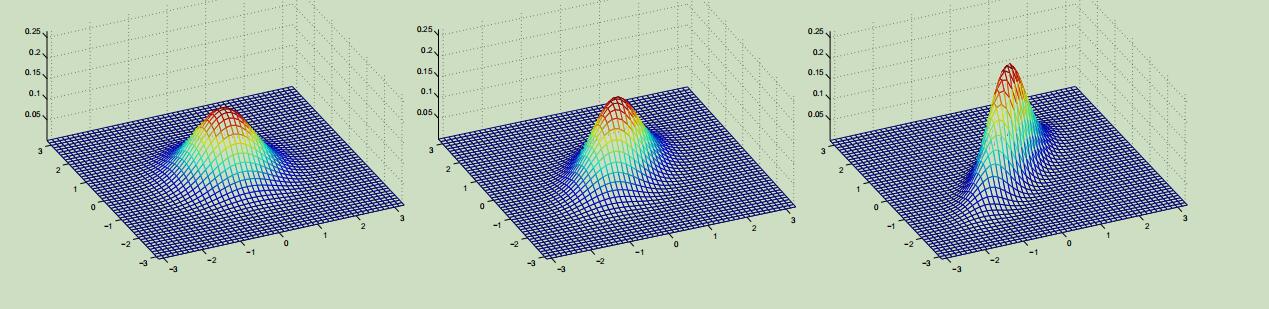
再给定二维投影的另一数据来当做例子：
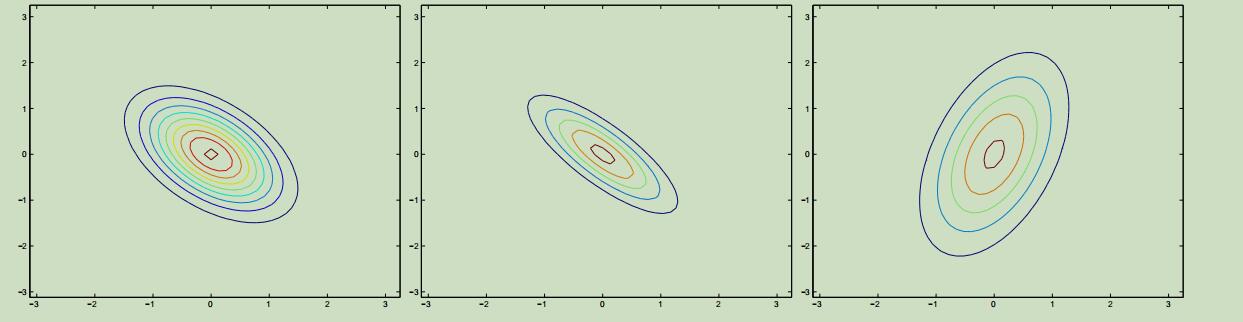
上面最左边的图减小了协方差矩阵副对角线的值，可以看到它在反方向进行了“压缩”；在第最右边的途中，我们改变了协方差矩阵主对角线上的值，图像变成了椭圆。
现在让我们来提供另一组对照例子，固定协方差为单位矩阵，通过改变$\mu$，来观察变化
高斯判别分析模型（Gaussian Discriminant Analysis model）
当对一个具有连续随机输入变量x的分类问题进行建模时，我们可以使用GDA模型，其中对p(x|y)建模使用多元正态分布 。GDA模型为：
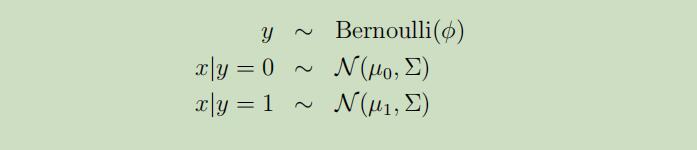其展开式为：
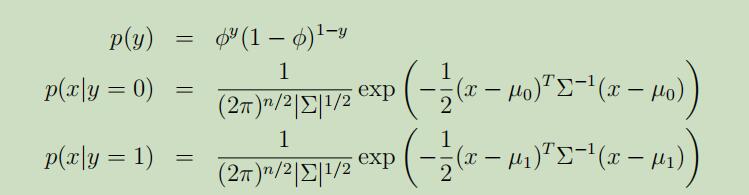
Σ为协方差矩阵
变量的对数似然函数如下：
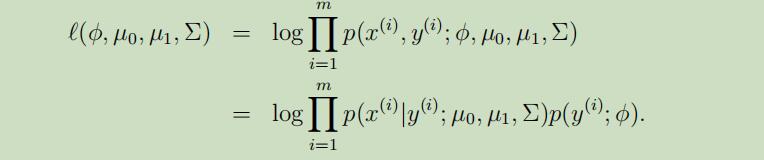每个参数的极大似然估计如下：
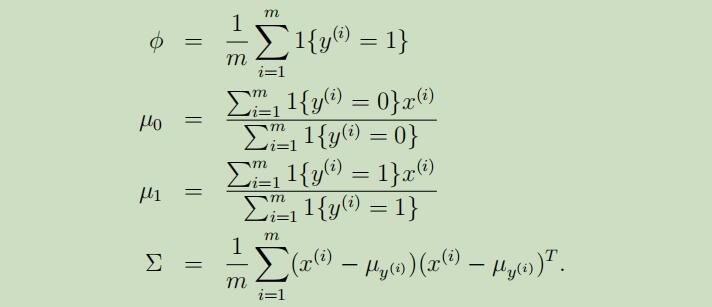
GDA算法的效果图如下：
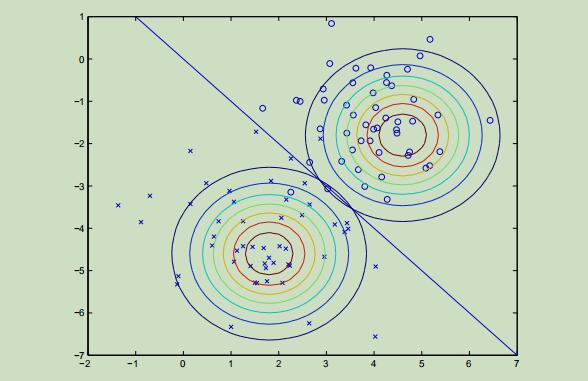
讨论：GDA与逻辑回归
下图是通过GDA建模建立的两分类的高斯分布图像，然后利用贝叶斯公式来表示出p(y|x)，会得到一条很像逻辑回归中sigmoid函数的曲线：
一般来说，GDA模型和逻辑回归会对先相同的数据集给出不同的决策曲线，那我们选择哪个呢？
先观察如下图的结论：
GDA是比逻辑回归更强 的假设，即若数据集满足多元正态分布，那么就一定可以导出逻辑回归；但是，逻辑回归 却不一定能导出GDA。故，基于这点，在以下情况GDA模型会比逻辑回归更好： 1.满足GDA的假设，即数据集近似于多元正态分布。 2.满足多元正态，且数据集非常大时，没有其他算法比GDA更准确。当数据集很小时，仍然比逻辑回归要好。
相反，因为逻辑回归是较弱一些的假设，所以逻辑回归对不正确的建模假设有更高的鲁棒性和更低的敏感性。故在数据集不是多元正态分布时会比GDA好。
朴素贝叶斯（Naive Bayes）
下面用文本分类 中的垃圾邮件过滤 来作为一个例子讲解朴素贝叶斯。
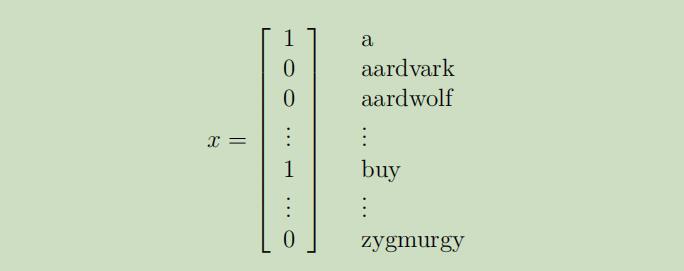
首先，我们定义特征向量x为一个词汇表，若单词出现过则相应的分量为1，否则为0：
为了建立一个生成模型，即建模$p(x|y)$，需要做一个特强假设：给定y下的条件分布$x_i$是独立的。
该假设被称为Naive Bayes(NB) assumption，该生成算法被称为朴素贝叶斯分类器
由此假设，得到：
之所以称之为特强假设，是因为其在现实中肯定不成立，语句中单词的上下文肯定具有一定的联系。但是即使假设明显错误，但是使用朴素贝叶斯算法仍有很不错的准确度。
在此模型中， 参数定义如下：
$\phi_{j|y=1} = p(x_j = 1|y = 1)$ $\phi_{j|y=0} = p(x_j = 1|y = 0)$ $\phi_y = p(y = 1)$
通常，训练数据集为$\lbrace (x^{(i)}, y^{(i)}); i =1,…, m\rbrace$
故，联合似然函数 可以写为：
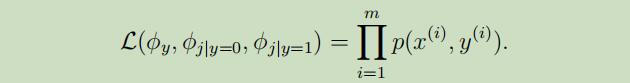参数的极大似然估计为：
在对以上参数进行了拟合之后，为了对新的样本进行预测，需要先进行如下运算：
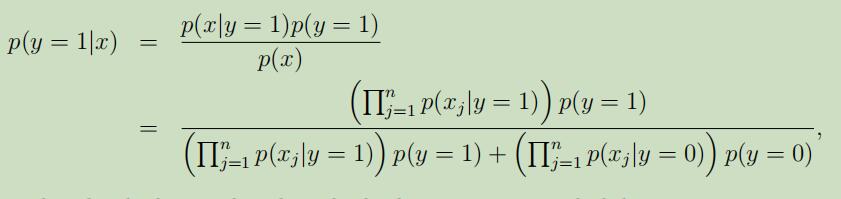并且挑选具有更高后验概率的那一个分类。注意，这里并不需要计算p(x),只需比较上半部分大小即可 。
最后，因为在本例中特征$x_j$为二元的，为了能将其推广到多元{1, 2,..., kj}，我们将不再使用伯努利而是多项式来建立模型$p(x_j|y)$，即使输入的属性是连续的，我们也可以通过如下方法将其离散化。当输入的属性是连续且不服从多元正态分布，将其离散化并使用朴素贝叶斯相较于GDA来说，是一个更好的选择。
拉普拉斯平滑（Laplace smoothing）
为什么需要拉普拉斯平滑？
假设词“NIPS”从未在你的邮件（垃圾邮件和非垃圾邮件）中出现过，并假设“NIPS”在词典中的顺序为第3500个，那么我们可以得到参数$\phi_{35000|y}$的极大似然估计为：
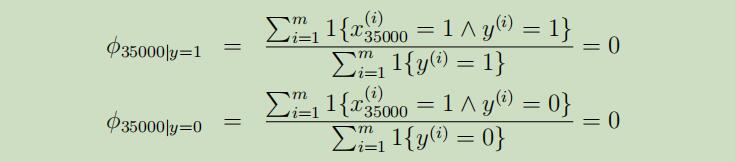所以，我们就可以仍未“NIPS”这个词将不会再垃圾邮件中出现，也不会再非垃圾邮件中出现，是这样吗？？？显然不是！
出现这种问题的原因是样本的限制，因为你不可能通过少量的样本，就把所有的邮件信息全部都建模，这是一件不可能的事情
因此，当我们利用朴素贝叶斯算法来计算“NIPS”的后验概率时，因$ p(x_{35000}|y)$ =0 得到：
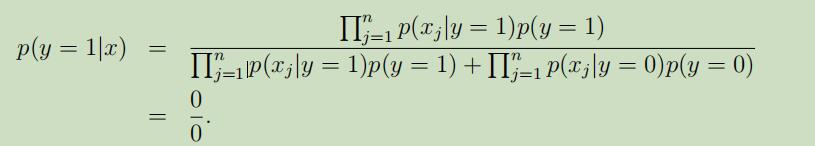这时结果就是未知的了。
换而言之，通常情况下，来根据有限的样本来估计事情的发生率，一般这样计算：
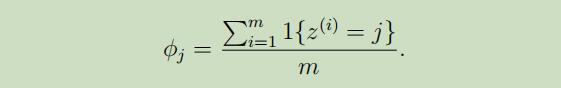但当样本中的数据出现连续的0或1时，就会出现两极化的问题。
下面引出拉普拉斯平滑技术，来解决这个问题：
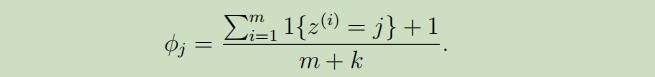
下面将拉普拉斯技术应用到朴素贝叶斯中：
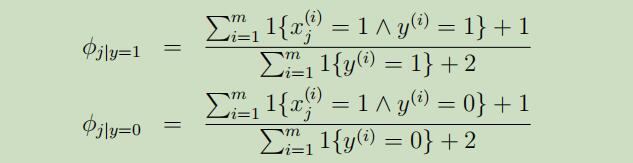
文本分类事件模型
为朴素贝叶斯模型的多项式形式，即不仅统计该词是否出现，还统计了出现个次数。
下面我们将介绍一种特定用于文本分类的一个模型，在文本分类领域，它会比朴素贝叶斯模型更好。
在文本分类的特定语境中，朴素贝叶斯使用的是多元伯努利事件模型，在此模型中，假设收到的下个邮件是否垃圾邮件是随机的，且发送的内容中，每个单词都是相互之间独立的。因此给定一条消息，它的概率是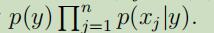
在此模型中，首先需要更改如下定义：$\lbrace x_1,…,x_n\rbrace$为邮件中的词集合，其中n为邮件中词的个数。随后，通过多项式分布$p(x_1|y)$来生成$x_1$，接着再从多项式分布生成与$x_1$独立的$x_2$，直至$x_n$。
最后，这个邮件的概率同上面所描述的一样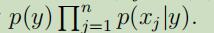，但有了不同的含义。尤其是这里$x_j|y$现在是多项式而不是伯努利分布。
在参数设定 上，仍和之前的一样： $\phi_y = p(y) ;\phi_{k|y=1} =p(x_j = k|y = 1) ;\phi_{k|y=0} = p(x_j = k|y = 0)$ 但是在这里我们已经假设过，对于不同的$j$，$p(x_j=k|y)$的结果是相同的（该分布不依赖于词的位置）。
当给定训练集$\lbrace (x^{(i)}, y^{(i)}); i = 1,…, m\rbrace$时，似然函数 如下：
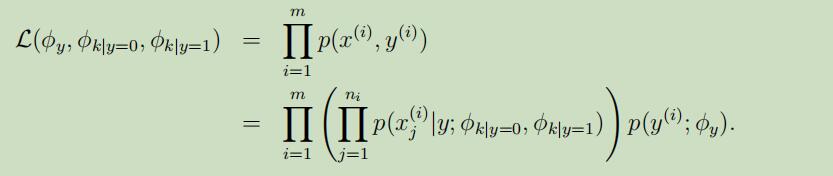
参数的最大似然估计值：
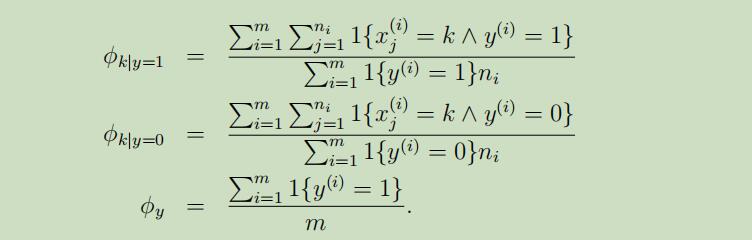
其中$n_i$为第i个样本具有的单词长度
使用了拉普拉斯平滑 后的参数极大似然估计值如下：
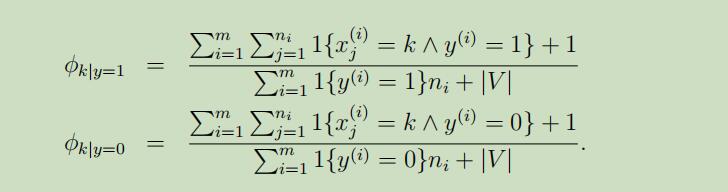
总结：虽然不是最好的分类算法，但朴素贝叶斯的结果常常惊人的好，基于它的简易性，常是人们的首选。
高斯朴素贝叶斯
当特征是连续变量的时候，运用多项式模型就会导致很多$P(x_i|y_k)=0$（不做平滑的情况下），此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，应该采用高斯模型。
例如下面这个例子，假设标签y=0代表男性，标签y=1代表女性，特征$x_1$代表身高（英尺），特征$x_2$代表体重（磅），特征$x_3$代表脚掌尺寸 x/y|$x_1$|$x_2$|$x_3$|
-
y=0 6 180 12 y=0 5.92 190 11 y=0 5.58 170 12 y=0 5.92 165 10 y=1 5 100 6 y=1 5.5 150 8 y=1 5.42 130 7 y=1 5.75 150 9
因此，此时的贝叶斯目标函数为 \(l(\theta)=\prod_{i=1}^{m} p\left(x^{(i)}, y^{(i)}\right)=p(x_1|y)p(x_2|y)p(x_3|y)p(y)\) 这里假设 \(x_i \| y=0 \sim \mathcal{N}(\mu_{i}, \sigma _i)\) \(x_j \| y=1 \sim \mathcal{N}(\mu_{j}, \sigma _j)\)
后面的参数更新及预测操作和之前一样了。
