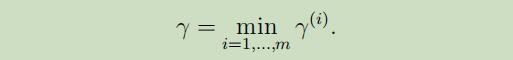网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes3.pdf
Lecture 6 -Neural Network,Support Vector Machines.
Introduction of Neural Network
分为输入层、隐藏层、输出层，隐藏层中的节点使用sigmoid函数，每一层的计算如图：
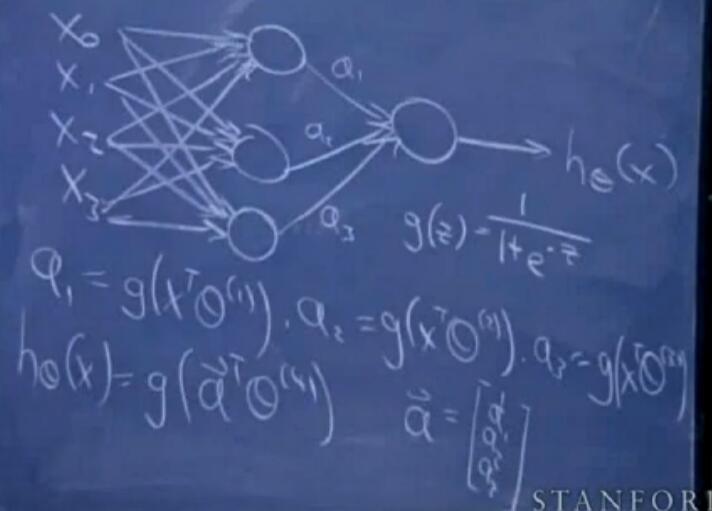
吴老师只是在这里简单的介绍了下神经网络，在《word2vec-中的数学原理详解》中对此有更为详细的讲解。
Margins：Intuition
当给定两个类（如正负类）和划分这些类的直线时，如下图，你会觉得哪一条直线更好？
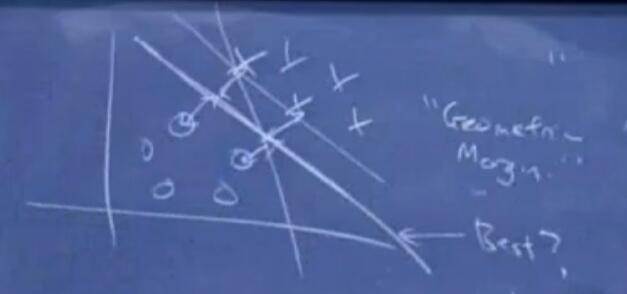
毫无疑问，直觉会告诉你中间那条线最好，但是为什么呢？因为直觉上告诉我们这条线距离两类最远。这就引出了这一部分内容的主题：Margins。
在逻辑回归中，如果$θ^Tx»0$，那么可以很自信的预测结果为1，若$θ^Tx«0$，那么可以很自信的预测结果为0。相反同理，如果当y=1时，$θ^Tx»0$，y=0时，$θ^Tx«0$，那么可以认为找了一条很好拟合数据的曲线。
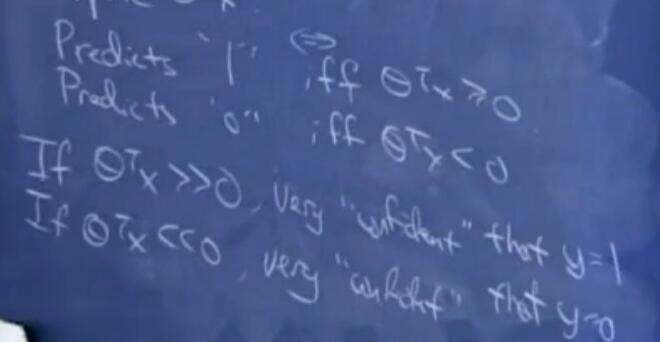通过这些可以映射出一个对所有训练样本都十分信任的分类集合，这看起来是我们所要追求的一个很好的目标，在接下来我们将用functional margins来规范化这个思想。
为了体现这种“直觉”思想，我们给出一个例子来体现：
x代表正例，o代表负例，直线是决策界限，也被称作分割超平面
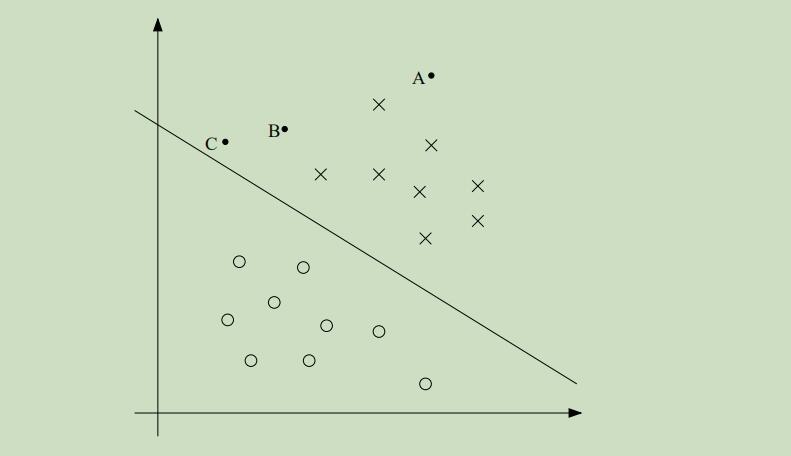图中，ABC为三个样本点，因为A点距离决策界限距离很远，故可以十分自信的认为A点属于正例；C点虽然在界限的右边，按照界限划分来说是属于正例，但是只要这条决策界限发生一点小的变动，C点就有可能被划分为负类。更宽泛的说，离这条分割线越远，对我们的预测结果就可以更加的自信。
通常，我们会认为对于给定的训练集，寻找到一条能够做出全部正确和自信的界限（不同于上图较为粗糙的界限）会非常的好。
新的符号（Notation）
标签y∈{−1,1}来表示标签分类，线性分类器 的参数是w，b（不再是向量θ），分类器如下：
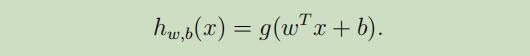其中g(z) = 1 if z ≥ 0;g(z)=-1 if z<0。并且这次把插入项给分离了出来，b取插入项θ0，w取值$f[θ_1,..,θ_n]^T$.由g(z)可知，我们的分类器只能取值1或者-1。
函数和几何距离(Functional and geometric margins)
给定训练集 $(x^{(i)}, y^{(i)})$，Functional margin定义如下：
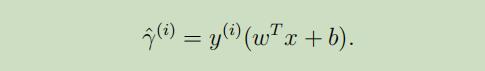
为了能让函数距离能够很大 ，当$y^{(i)}=1$时，$w^Tx + b$需要一个很大的正数；当$y^{(i)}=-1$，$wTx + b$需要一个很大的负数。当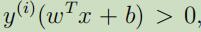
时，可以说我们对于此例的预测是正确的。
因此，一个很大的函数距离能够表示一个自信且正确的预测。
但是，函数距离同时也有一个问题，当我们把w和b替换为2w和2b时，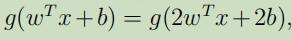
的值将不会改变；同时这样的替换，也会导致函数距离是原来的2倍 ，但是最后分类器的值却不会改变 。因此这就必须对w和b进行正交化。
同时，我们还把函数距离定义为所有函数距离的最小值：
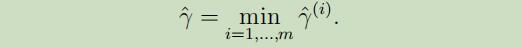
至于几何距离，先看下图：
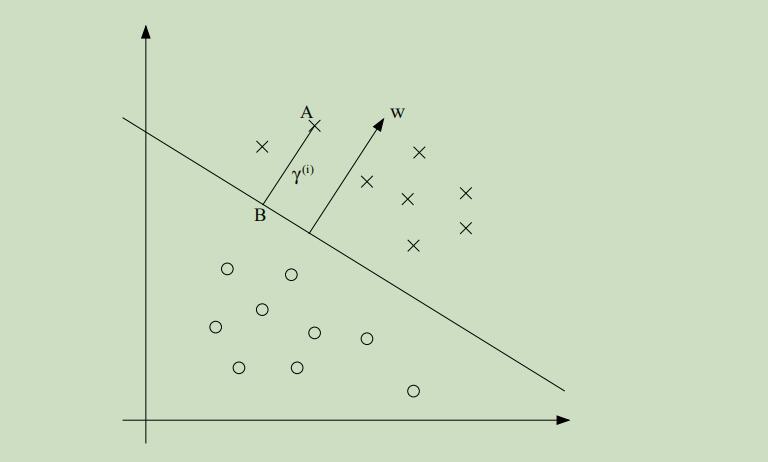
γ(i)为样本点A和界限上的点B之间的距离，w是参数向量，w/||w|| 是单位法向量
点B可以用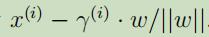
来表示，由于界限上所有点都满足$w^Tx + b = 0$，故：
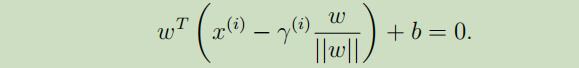其中，$γ^{(i)}$可以表示为：
因为上式是专门为在分界线的正侧导出的，所以推广开来可得：
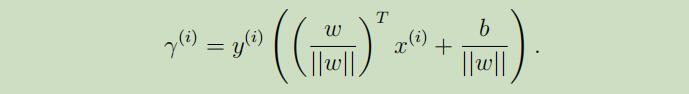
这里谈论下函数距离和几何距离的联系：如果另
||w|| = 1，那么几何距离就是函数距离。几何距离不会受到w和b倍数的变化而变化。因为几何距离参数的不变性，我们可以对w施加任何的条件限制且不改变重要的东西。
最后，同函数距离，几何距离被称为训练集中最小的那个几何距离：
