网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes3.pdf
Lecture 7 -Support Vector Machines. Kernels.
最优边距分类器（The optimal margin classifier）
给定一组线性可分 的训练数据集，怎样才能找到那个具有最大几何距离的超平面 呢？我们给定以下优化问题：
可解释为：最大化函数距离，并保持其余每个点的函数距离都大于此函数距离。其中||w||=1的目的在于将函数距离转化为几何距离，因此将求解(w,b)找到满足条件的最大几何距离
但是上面的优化问题其实是非凸问题的一种，因此很难将其直接扔进优化软件中寻找最优解。
所以，我们将转化上述问题至一个更好的优化目标：
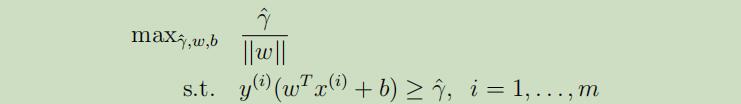
因为几何距离=函数距离/||w||，故避免了上面的||w||=1的限制。但是这仍然是一个非凸问题，仍然没有任何的优化软件可以用来寻找最优解
现在让我们继续寻找更好的优化目标：
首先，令函数距离等于1：
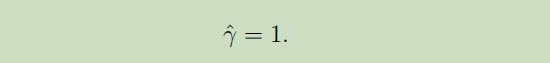
因为函数距离因为其(w,b)倍乘导致结果倍乘的这个性质，只要对(w,b)除以相应的结果，就很容易的得到函数距离等于1.
有了函数距离等于1后，最大化$\hat{\gamma}/||w|| = 1/||w||$的任务就变成了最小化||w||^2，由此优化目标就变成了：
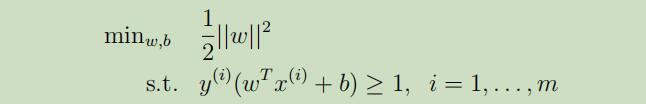
由此，我们就获得了可以被有效解决的优化问题，其变成了只有线性制约的凸性二次优化问题，可以使用商业二次编程（QP）代码来解决。
虽然我们在这里称之为问题被解决了，但是我们仍要对其 进行更广泛的讨论。我们接下来先岔开此话题讨论下拉格朗日对偶性，这将引出我们优化问题的对偶形式，它在使用kernels将优化边距分类器能在非常高维的空间中仍然效率很高。对偶形式可以导出一个能解决上述优化问题的高效算法且比QP软件好的多。
拉格朗日对偶性（Lagrange duality）
这里拉格朗日乘数法不再进行介绍，下面介绍的是拉格朗日乘数法的推广形式，即限制条件包括了不等式和等式。 考虑如下原始优化问题：
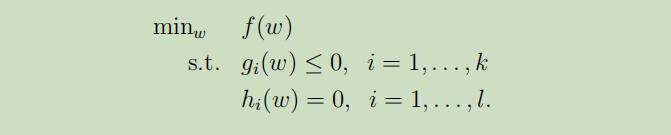为了满足以上条件，定义广义拉格朗日乘数公式为：
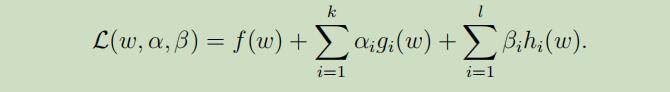
αi和βi为拉格朗日乘数
考虑如下等式：
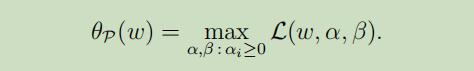当w不满足限制条件时，可以得到：
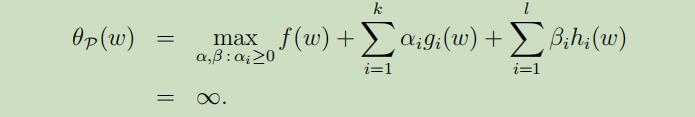进一步可以得到：
因此，我们考虑如下最小化问题：
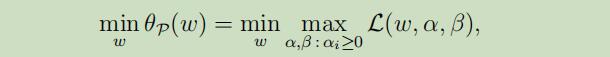发现其和原始优化问题 一样，令
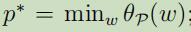为原始优化问题的值。
现在让我们看下面略微不同的问题;
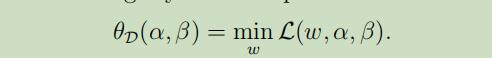
下标D表示“对偶”
下面展示对偶优化问题：
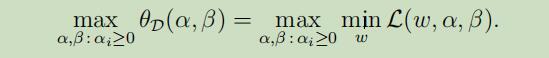这里令
这与源石优化问题仅是min与max互换了位置，且有如下定论：max min<=min max
故，原始问题和对偶问题之间的联系如下：
在某些条件下，我们可以得到
d*=p*，这可以帮助我们把对偶问题转化为原始问题。对偶问题在支持向量机中和最优间隔分离器中具有很多性质来使用。
为了导出这些条件 ，我们先假设$f(w)$和$g_i(w)$是凸函数，$h_i(w)$是仿射函数，且$g_i(w)$是严格可执行的，即存在w使得所有的$g_i(w)<0$。
有了以上假设后，就一定存在w*,α*,β*满足KKT条件；w*是原始问题的解，α*,β*是对偶问题的解
当w*,α*,β*满足KKT条件后，这些都将是原始问题和对偶问题的解
上面第3个等式叫做KKT对偶补充条件，当gi(w)=0时，其被称之为活动制约（这时αi可以是0或非零，但是实际上，通常αi和gi有一个是非0的）。这将是只有少量支持向量的SVM算法的关键所在。
这部分内容推荐讲义和视屏相互补充，不太容易理解。
最优间隔分类器（接着前面的）
在之前的部分，我们寻找出了最有间隔分类器的优化目标：
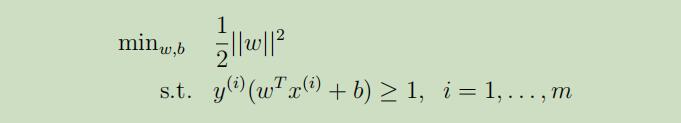
其中，我们可以把限制条件改写如下：
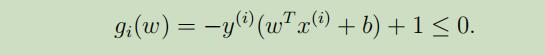
从KKT补充条件可推之，只有当αi>0的时候，gi(w)=0也就是函数间隔为1。
观察下图，实线为超平面，虚线为函数距离等于1的线 ：
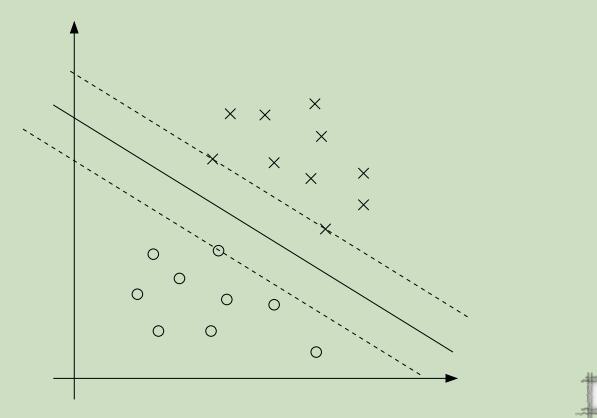
同样由KKT补充条件可以推之，有三个点的函数间隔为1，即只有三个αi!=0。这三个点被称作支持向量。
现在我们将原始优化目标写成拉格朗日乘式的形式：
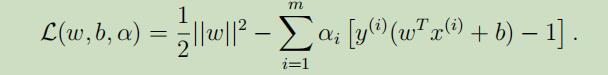
通过对w和b求偏导，对L(w, b, α)进行最小化 ，来得到对偶问题：
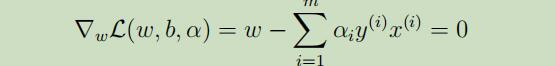解得
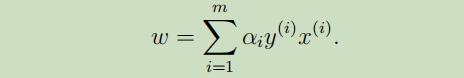同样
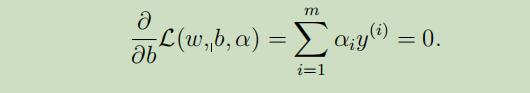
到这里，我们将上面得到的w，b的值带入L(w, b, α)中得到其最小值：
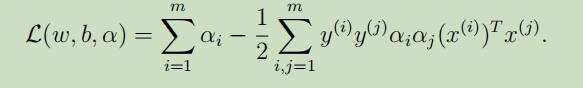
综上所述，得到了对偶优化问题如下：
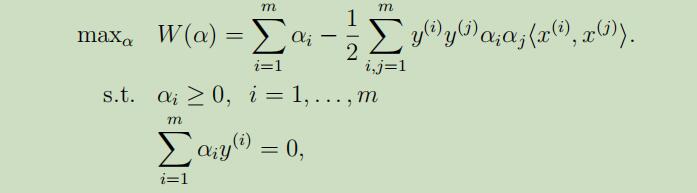
当我们可以验证p*=d*和KKT条件都在此问题中满足，因此我们可以解决对偶问题来代替解决原始问题，并且我们有特定的算法来解决对偶问题。从上面导出的w*我们可以直接导出插入项b为：
现在假设我们已经训练模型得到了拟合的参数，我们要对输入点x的输出进行预测，如果我们计算出的wT x + b比0大的多，那么可以预测y=1，从而得到：
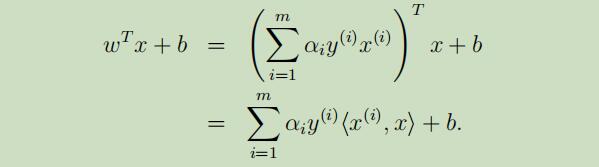
因此当我们进行预测时，仅仅需要计算x和训练集中点的内积，并且αi在本例中只有三个点不等于0（那三个支持向量），所以在整个训练集中，我们仅仅需要这些支持向量就可以预测出最后的结果。
