网易公开课视频地址：http://open.163.com/movie/2008/1/M/C/M6SGF6VB4_M6SGHFBMC.html?frm=record 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes3.pdf
Lecture 8 - Kernels.SMO algorithm.
核(Kernels)
机器学习里的 kernel 是指什么？https://www.zhihu.com/question/30371867/answer/73428260
现在让我们回到之前线性回归的讨论之中，我们根据输入x（房屋大小）使用特征x,x^2,x^3来获得一个三次函数，为了区分这两种类型的变量，我们把原始输入值称之为问题的属性 （房屋大小x），把原始输入经过映射后的那些将要在学习算法中使用的量 称之为输入特征 ,同时把原始输入到输入特征之间的映射φ称之为特征映射 。例如：
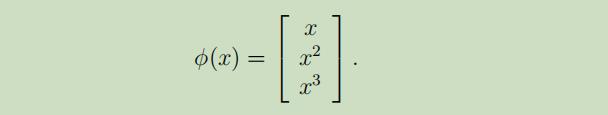
SVM算法使用的是特征φ(x)，因此我们将在所有地方都使用φ(x)而不再是x
因为算法可以使用内积<x,z>来完全表示，我们可以将所有的内积替换为<φ(x), φ(z).>。当有了映射$\phi$后，定义核（Kernel） 如下：
这意味着我们可以将算法中所有的<x,z>简单的替换为K（x,z）
当$\phi(x)$是特别高维度的向量，即使映射本身特别难计算，计算出K(x,z)将不会那么的难。 基于这种设定，即使没有很明确的表示出映射$\phi(x)$，通过很高效的计算出K(x,z)，我们可以使得SVM在非常高维的空间中进行学习。
为了解释这些，举一个例子：
假设x，z都是n为向量，且
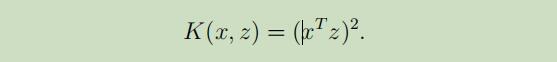将上式展开为：
如果n=3时，特征映射被给如下，那么我们可以得到$K(x,z)=\phi(x)T\phi(z)$
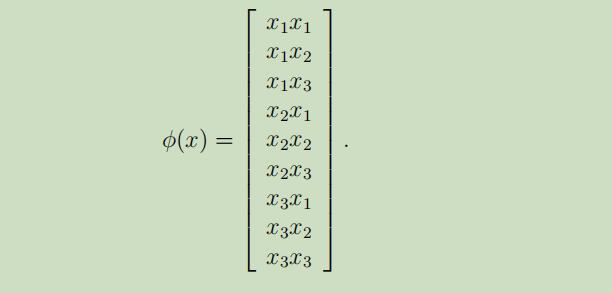
注意，即使计算高维向量需要$O(n^2)$的时间复杂度，但是根据输入属性的线性，找到K(x,z)只需要$O(n)$的时间复杂度.
对于一个相关的kernel，我们考虑
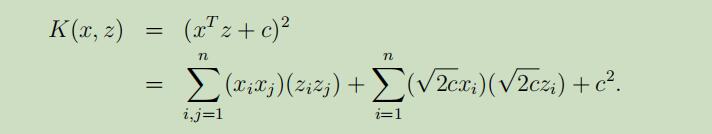找到n=3时的特征映射如下：
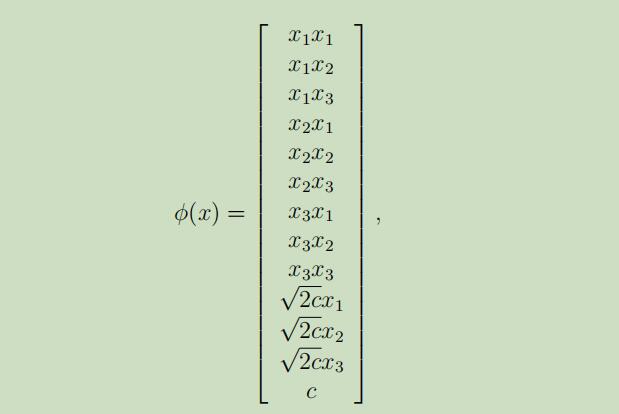
其中，参数c的作用是控制xi（一阶）和xixj（二阶）之间的相对权重
更宽泛的说，kernel $K(x, z) = (x^Tz + c)^d$ 等同于一个到$(^{n+d}_ d)$特征空间的特征映射，所有单项式$x_{i_{1}} x_{i_{2}} \dots x_{i_{k}}$的阶最多到d。然而尽管SVM要在$O(n^d)$的多维空间中运行，在没有给定确切特征向量的情况下，计算K(x, z)仍然将只花费O(n)的时间。
现在让我们换一个略微不同的视角看到kernels，直观上来说，如果$\phi(x)$和$\phi(z)$比较接近，那么$K(x,z)=\phi(x)^T\phi(z)$可能会大；相反的，如果$\phi(x)$和$\phi(z)$距离很远（几乎垂直），那么kernel将会很小。所以，我们可以把kernel当作$\phi(x)$和$\phi(z)$相似程度的测量手段。
例如，我们可以选用如下高斯kernel 来当作测量x与z相似度的手段，并作为kernel应用到SVM中。 $K(x, z)=\exp (-\frac{|x-z|^{2}}{2 \sigma^{2}})$
下面来检验kernel的合法性，即是否存在$\phi$，使得K(x,z) = <φ(x),φ(z)>。
假设有m个点的集合$\lbrace x_1,…,x_m\rbrace$，kernel K为$m\times m$阶的方阵,$K_{ij}=K(x_i，x_j)$。
因此，可以推导出下列式子：
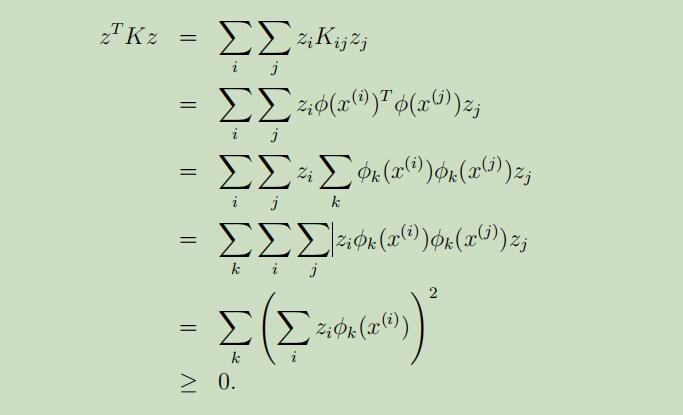
现在让我们回顾线代中，正定矩阵的定义，存在z>0,使得zTkz>0，故K是正定矩阵。而这里z是随机变量，故K是半正定矩阵，相反也成立。此条件为充要条件
定理（Mercer）:如果K是n阶方阵，对于任意的$\lbrace x_1,…,x_m\rbrace$，K是一个有效的kernel的充要条件是，K是半正定矩阵。
https://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html
通过Mercer定理，可以让我们不必在找到一个符合kernel的特征映射$\phi$，而是对kernel矩阵进行判定即可得知kernel是否有效。
接下来，让我们简单的讨论些kernels在其他例子中的使用。在数字验证码识别问题 中，在SVM中使用简单的多项式kernel $K(x,. . . z)=(x^Tz)^d$ 或者高斯kernel 都可以获得非常不错的效果，甚至在没有任何关于视觉和邻接像素先验知识并且输入属性x是256维度图片像素密度向量的情况下，它的表现尤其惊人的好。在字符串分类问题 中，很难去构造一个合理的“小”的特征集合，尤其是当字符串长度还未定时；然而，如果令$\phi(x)$成为k长度的字符出现次数，在英文信封中将会得到$26^k$个这样的字符串，这很难去有效的计算它。但是使用字符串学习算法(dynamic programming-ish)，不给出明确的特征映射$\phi$，高效地计算kernels是可能的。
吴老师最后还给出了一个小技巧，叫kernel trick ：如果您的学习算法可以写成只有输入属性向量之间内积的形式<x,z>，就可以将其替换为K(x,z)，然后你就会“奇迹般”的发现你的算法也可以在高维度空间中高效的运作。
线性不可分
在讲这部分之前，老师对SVM算法做了一个形象性的描述。如下图：左边是在一维上的一组线性不可能的数据样本，通过高斯kernel将一位样本映射到了高维空间中，然后在高维度空间中使用SVM算法再对数据样本进行分割。
虽然说，将数据映射到了高维空间很大程度的加大了其线性可分的可能性，但是仍然不能保证其在高维是可分的。并且还存在一个问题，有时并不能很确定分割超平面就是我们所想要寻找的那样，例如下图：
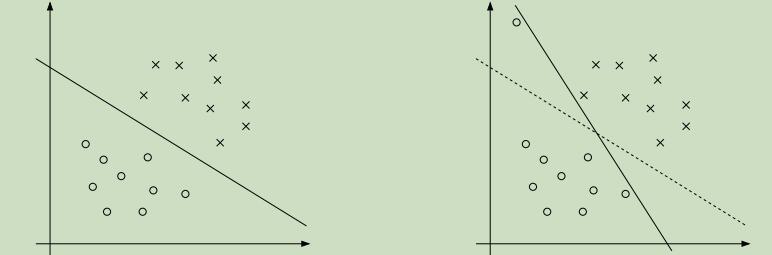
从图中可以看出，当原先样本加了一个较为偏离的样本点后，超平面发生了很大的变化，并且其距样本点的距离离变小了很多。
为了能够是使算法应用于线性不可分的数据集和降低对外入的点的敏感性，我们把之前的优化目标重新更定如下：
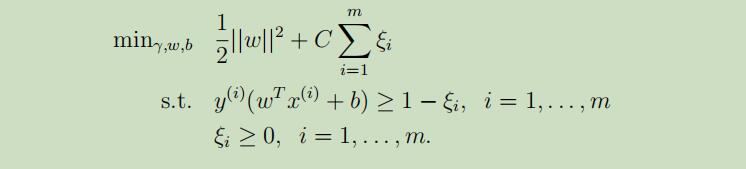
这允许我们的函数距离小于1并且当函数距离为1 − ξi时，需要为目标函数增加一些消耗Cξi。参数C控制的是最小化||w||和确保函数距离小于1之间的相关权重。
像之前一样，写出拉格朗日乘法公式如下：
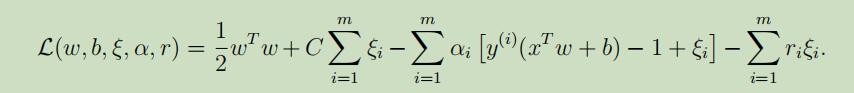
其中，α和r是拉格朗日乘数
将w，b的导数设为0后，将其带入上面的优化问题中，化简可得优化问题的对偶形式：
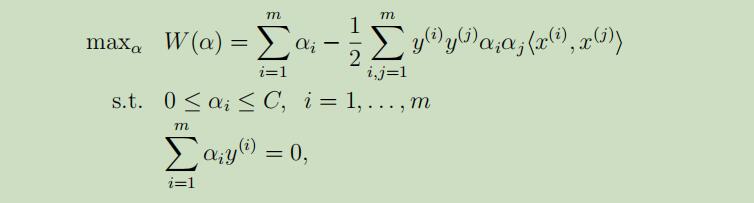
同时，KKT补充条件（将用于测试SMO算法是否收敛）也要修改为如下：
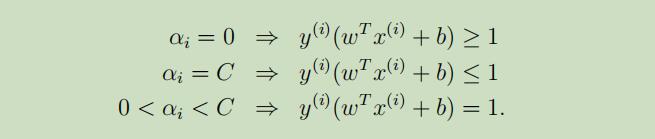
故，在做完这一切后，剩下所需的就是一个能解决对偶问题的算法，将在后续讲解。
SMO（sequential minimal optimization）算法
在讲述SMO算法来解决SVM中的对偶问题前，先介绍一个新的求最值的优化算法。
坐标上升（coordinate ascent）算法
考虑如下优化问题：$\max _{\alpha} W(x)$
函数W(x)以m维的向量x为参数，$x=[α_1,α_2,…,α_m]$
在算法的每一轮中除了当前的参数$α_i$需要更新外，其他的参数都是固定的。算法如下：
在算法的每一轮中， 都对参数x中的一个维度进行更新，求出使函数W(x)值最大的那个参数值。例如第一次更新α1，第二次就在α1的基础上在更新α2，并以此类推。这样进行每一轮更新后，现有的参数值带入函数中都会比上一轮参数的函数值要大。
图中的椭圆曲线是我们想要优化的二次函数的轮廓，起始点为(2,-2)，椭圆中心即为二次函数的最大值。因此每次只更新一个参数，算法的更新是按照一个坐标轴来进行，图中显示的坐标上升并没有按照特定的步长来进行更新，事实上，参数更新的顺序或长短都是可以自己进行指定的。
这里与梯度上升和牛顿方法一起讨论下坐标上升： 坐标上升算法通常情况下会比其他两个方法要经过更多的步骤，坐标上升算法的主要优点是，当一个优化目标函数W非常容易在其他参数都固定，只对一个参数进行更新的情况下，在内层循环中αi的更新会非常的快。这一点在SVM算法中十分有用。
SMO算法
SMO算法是坐标上升算法的在SVM算法应用中的改进版，首先回顾我们需要解决的对偶优化问题：
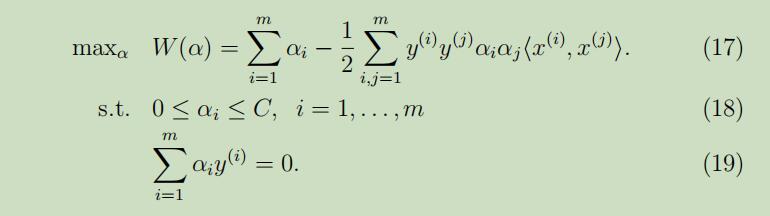在这里不同于上文讲的坐标上升算法的地方在于，需要满足限制条件(18-19)，如果我们保持除了α1外的参数固定来更新α1的话，将会出现如下问题：
$\alpha_{1} y^{(1)}=-\sum_{i=2}^{m} \alpha_{i} y^{(i)}$
当α2…αm都是固定的值时，α1在满足限制条件(18-19)的情况下也是个固定的值，因此我们不可能对α1进行更新。
假设现在令$\alpha_{3}, \dots, \alpha_{m}$固定，使用两个参数αi和αj来最优化W(x)，从限制条件19中我们可以得出如下等式：
$\alpha_{1} y^{(1)}+\alpha_{2} y^{(2)}=-\sum_{i=3}^{m} \alpha_{i} y^{(i)}$
因为等式右边都是固定的值，这里我们将其表示为常量$\zeta$：$\alpha_{1} y^{(1)}+\alpha_{2} y^{(2)}=\zeta$
现在我们可以把关于α1和α2的限制条件在坐标系中显示出来，如下：
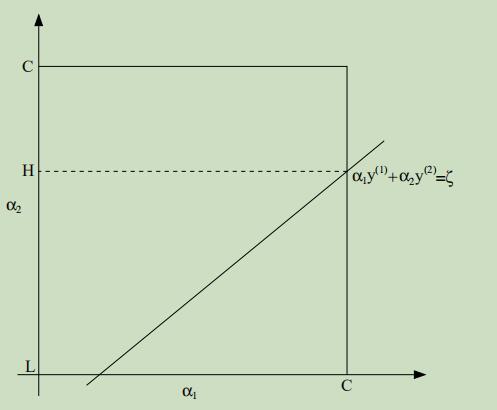从限制条件18可知，参数α1和α2必须落在如图的实线正方形中，图中的斜线段正是两个参数必须落下的地方以满足限制条件19。接着我们可以让上面的等式用α2来表达α1：
$\alpha_{1}=(\zeta-\alpha_{2} y^{(2)}) y^{(1)}$
（$y^{(1)} \in\lbrace -1,1\rbrace$，因此$(y^{(1)})^{2}=1$）
然后，把参数带回到函数W(x)中：
$W(\alpha_{1}, \alpha_{2}, \ldots, \alpha_{m})=W((\zeta-\alpha_{2} y^{(2)}) y^{(1)}, \alpha_{2}, \ldots, \alpha_{m})$
把$\alpha_{3}, \dots, \alpha_{m}$视为常量，我们可以验证这是α2的二次函数，例如它通常可以表达为$a \alpha_{2}^{2}+b \alpha_{2}+c$的形式。而二次函数的极值求解起来是十分容易的，我们可以使用$\alpha_{2}^{n e w, u n c l i p p e d}$来表示α2的解，如果此时的解并没有满足所需要的约束条件（即图中方形框中的斜线上），我们可以对α2进行下分解来得到符合条件的解：
然后我们可以使用最终求得的解α2带回到等式中，就可以求出最优解α1.
因此在满足所需的限制条件的情况下，如果我们想要更新某一个参数αi，则我们必须同时更新两个参数在每一轮中，正是这个原因促使了SMO算法的产生，其可以简洁的描述为：
Repeat till convergence{
1. 选择下一步要更新的参数对αi和αj
2. 在保持其他参数都固定的情况下，使用参数αi和αj来重复优化W(x)
}
测试算法是否收敛的条件为，检查KKT条件(14-16)是否满足一些tol。这里tol是收敛容忍参数，通常被设置在0.01到0.001之间（具体看论文和伪代码）
SVM的hinge loss和梯度下降实现
1.Hinge损失函数
首先我们来看什么是合页损失函数（hinge loss function）：
下标”+”表示以下取正值的函数，我们用z表示中括号中的部分：
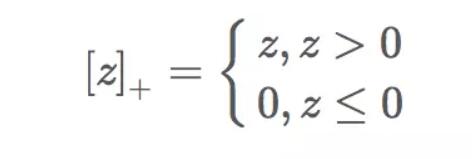也就是说，数据点如果被正确分类，损失为0，如果没有被正确分类，损失为z。
合页损失函数如下图所示：
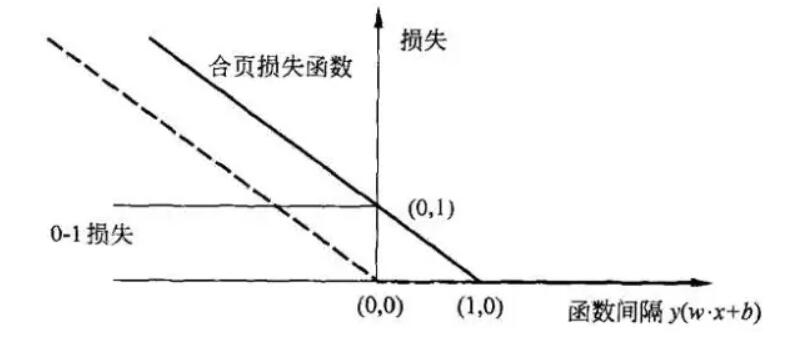
来自https://www.jianshu.com/p/fe14cd066077
2、SVM损失函数
SVM的损失函数就是平均合页损失函数加上L2正则,其Kernel化的推导过程如下：
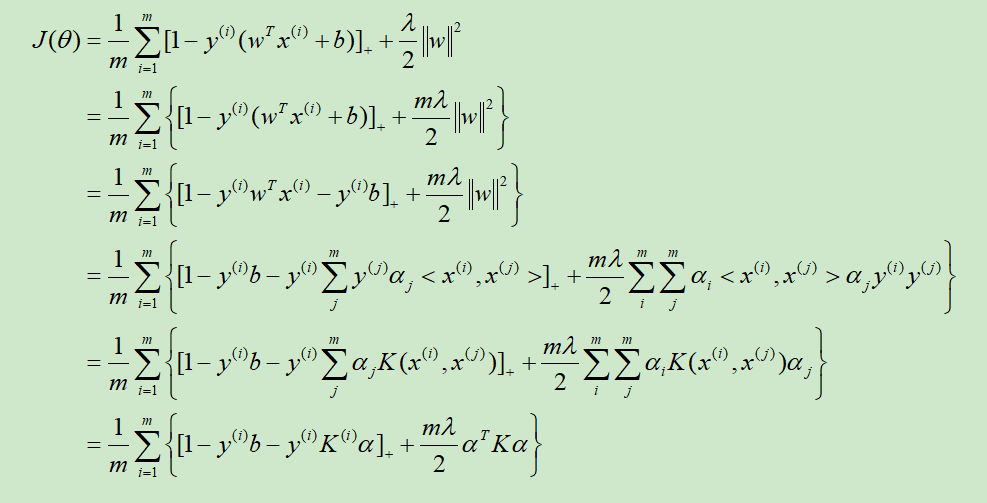
在前四步中，参数w取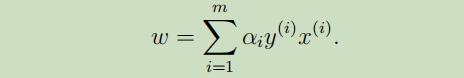
然而在NG的推导中，w取的为$w=\sum_{i=1}^{m} \alpha_{i} x^{(i)}$，去掉了$y^{(i)}$，如后两步所示，还不清楚为啥。
3. 随机梯度下降
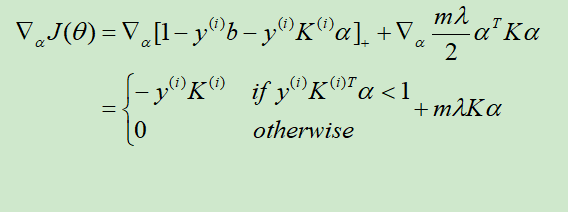
注意这里NG同时还扔掉了参数b，不知道有没有影响
训练完成后得到大小为m的参数$\alpha$.
4. SVM测试
假设训练集样本大小为m_train,测试集大小为m_test。
在NG扔掉了$y^{(i)}$和参数b后，在给定测试集中的样本$x^{(j)}$后我们所需要的预测仅为
$\sum_{i}^{m_train} \alpha_{i}<x^{(i)}, x^{(j)}>$
在使用训练集和测试集中的样本生成的$m_test \times m_train$维的Kernel矩阵后，对于测试集的样本$x^{(j)}$，我们的预测公式更新为
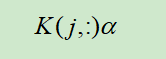然后在使用分类器，若上式大于0，为1，否则为-1.
