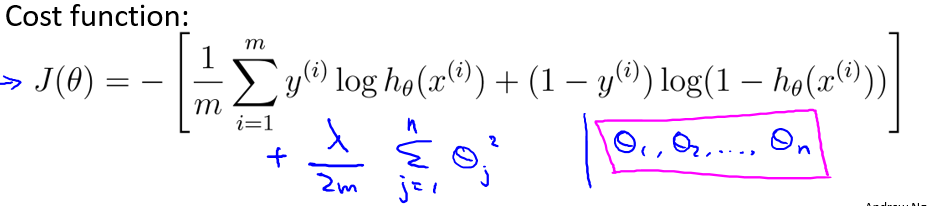网易公开课视频地址：http://open.163.com/movie/2008/1/U/O/M6SGF6VB4_M6SGJURUO.html 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes5.pdf

Lecture 10 - Regularization and model selection.

假设我们正在试图从一些不同的模型中选择一个去学习问题，例如我们可能使用多项式回归模型$h_{\theta}(x)=g(\theta_{0}+\theta_{1} x+\theta_{2} x^{2}+\cdots+\theta_{k} x^{k})$并决定k应该取什么值，如何才能自动的选择出一个能对偏差和方差进行折中的模型呢? 相对的，放在局部加权逻辑回归中就是如何选择参数$τ$，放在SVM中就是如何选择经过$\ell_{1}$ -regularized的参数$C$.

为了寻找具体的证明方法，在之后我们假设我们要从模型集合$\mathcal{M}=\lbrace M_{1}, \dots, M_{d}\rbrace$中选择，其中$M_{i}$代表着几阶的多项式回归模型。

1. 交叉验证

像平常一样，给定义个训练集$S$，现在让我们使用经验风险最小化来做模型选择，算法如下：

对训练数据集$S$使用每个模型$M_i$来训练，得到对应的假设$h_i$
挑选出具有最小训练误差的假设

请注意，这个算法是无效的。因为对于更高阶的多项式，它将能够更好的对训练数据集S进行拟合，这个算法选择出来的模型总是具有高方差，高阶的多项式模型，并不是很好的选择

下面来看更好一些的算法，叫做hold-out交叉验证（也叫做简单交叉验证），如下：

随机将训练数据集$S$划分为70%的$S_{train}$和30%的$S_{cv}$。其中，$S_{cv}$称作hold-out交叉验证集
使用每个模型$M_i$对$S_{train}$进行训练，得到对应的假设$h_i$
选择并输出具有最小训练误差$\hat{\varepsilon}_ {S_ \mathrm{cv}}(h_{i})$的假设$h_i$

通过对没有经过训练的数据集$S_{cv}$进行测试，我们可以得到对于每个假设$h_i$泛化误差更好的估计，因此我们可以最后挑选具有最小估计泛化误差的模型。通常，我们使用$1 / 4-1 / 3$的数据集来做交叉验证，30%是很典型的选择。

可选择性的，步骤3可以被替换为，选择具有最小泛化误差$\arg \min _ {i} \hat{\varepsilon}_ {S_{\mathrm{cv}}}(h_{i})$的模型$M_i$，然后对于整个训练集$S$重新训练$M_i$。（这通常是一个很好的想法，但是有一个例外，那就是当学习算法对初始条件或数据非常敏感的情况下，$M_i$能在$S_{train}$上表现的很好，并不意味着它仍然将在$S_{cv}$上表现的很好，因此放弃重新训练的步骤可能是更好的选择）

简单交叉验证的缺点在于它会“浪费”掉大约30%的数据集，即使我们采用了可选的对整个数据集重新训练这一步，这将仍然可以视为我们只试图使用0.7m的训练样本来寻找一个好的模型，而不是整个训练样本。尽管当数据很丰富或者廉价的时候这是无所谓的，但是在一些数据十分稀少的学习问题（比如m=20）中，我们可以来做的更好一些。

这个方法叫做k重交叉验证，每一次只使用很少的数据：

随机将集合$S$均分为k个邻接的子集，将这些子集称为$S_{1}, \dots, S_{k}$
对于每一个模型$M_i$,我们对其做如下的评估：

2.1 For j=1,…,k

在$S_{1} \cup \cdots \cup S_{j-1} \cup S_{j+1} \cup \cdots S_{k}$（除了$S_j$的训练数据集）上对模型$M_i$进行训练，得到对应的假设$h_{i j}$

在$S_j$上对假设$h_{ij}$进行测试，得到$\hat \varepsilon_ {S_j}(h_{ij})$

2.2 计算$\hat \varepsilon_ {S_j}(h_{ij})$的平均值，来得到模型$M_i$的估计泛化误差
选择具有最小估计泛化误差的模型$M_i$,并试用其对整个训练集$S$重新训练。此时输出的x训练参数就是我们最后的算法结果。

通常我们选择重数k=10，这样我们每一轮所需要保留的测试集比简单交叉验证少的多，但是在计算上的代价是非常昂贵的。

如果当训练数据集真是非常稀少时，我们可以选择极端的策略，$k=m$。这时每一轮会对几乎所有的样本进行训练，只对一个样本进行测试，然后再将m=k时的误差平均起来，得到的就是我们所需要的当前模型的估计泛化误差。这种方法叫做leave-one-out 交叉验证

最后，即使我们介绍了这么多可以用来做模型选择的交叉验证版本，它们同样也可以简单的去用来评估单个模型或算法的性能。例如，如果实现了一些学习算法并且想要估计它在你的应用中表现的如何，交叉验证将会给你一个合理的方式来进行验证。

2.特征选择

在模型选择中一个特殊切重要的例子称作为特征选择。动机如下：设想你有一个监督学习问题有非常多的n个特征($n \gg m$)，但是你发现仅有一小部分的特征可能和你的学习任务有关，这时即使你对n个输入的特征选用的是简单的线性分类器（比如感知器），假设类的VC维度仍然会有$O(n)$的复杂度，因此过拟合将会成为一个潜在的问题。

在这种设定下，我们可以应用一个特征选择算法来降低特征的个数。给定n个特征，将会有$2^{n}$种可能的特征子集（n个特征中的每个特征都可以被子集包含或者排除），因此特征选择就可以看作为对$2^{n}$种可能模型的模型选择问题。但是对于很大的n值，枚举和比较所有$2^n$个模型的代价将会十分昂贵，所以会有一些典型的启发式搜岁程序来去寻找一个很好的特征子集。如下的搜索程序称作为前向搜索（forward search）：

初始化$\mathcal{F}=\emptyset$
重复｛

（a）For $i=1, \dots, n$，if $i \notin \mathcal{F},$ let $\mathcal{F}_{i}={\mathcal{F} \cup\lbrace i\rbrace}$。然后使用一些交叉验证方法来评估特征$\mathcal{F}{i}$

(b)设$\mathcal{F}$为步骤(a)中找到的那个最优的特征子集｝
选择并输出在整个搜索过程中评估出来的最优特征子集。

当$\mathcal{F}=\lbrace 1, \dots, n\rbrace$为所有特征的集合，或者当$|\mathcal{F}|$超过了提前设置的阈值时（想要使用特征数的最大值），算法的外层循环可以被终止。

上面这个算法可以被描述为包装（wrapper）模型特征选择的一个实例，这是因为算法的程序就是一层一层得来包装算法，并对每个不同的特征子集评估它的效能。除了前向搜索算法外，还有一种搜索算法可以用来寻找特征子集。这个和前向搜索十分相似的算法叫反向搜索，它是最开始使用所有的特征集合$\mathcal{F}=\lbrace 1, \ldots, n\rbrace$，并且每次从中删除一个特征直到$\mathcal{F}=\emptyset$。包装模型特征选择算法通常情况下工作的相当好，但是它的计算代价很昂贵，因为这需要它调用很多次所使用的学习算法。确实，完整的前向搜索（直到$\mathcal{F}=\lbrace 1, \ldots, n\rbrace$）将会调用$O(n^{2})$次这个学习算法。

过滤（Filter）特征选择方法给我们一种启发式，但计算更廉价的方式来选择特征子集。其思想为通过计算一些简单的分数$S(i)$来评估每个特征$x_i$对于分类标签y具有多少信息量。然后简单的选取k个$S(i)$最大的特征。

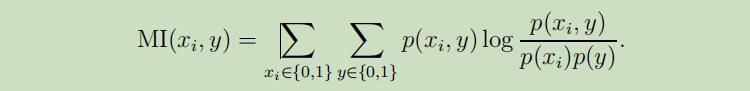
分数$S(i)$可以被定义为在训练数据集上测量的$x_i$和y之间相互关系的绝对值，这将导致我们选择那些和分类标签有强关联的特征。实际上，通常选择（特别是离散特征$x_i$）$S(i)$为$x_i$和y之间的相互信息量（mutual information）： （这个等式假设了xi和y都是二元值，是对其域上所有变量的累加）$p(x_{i}, y), p(x_{i})$ 和 $p(y)$都可以根据训练集的经验分布来估计出来。

相互信息量也可以被表示为Kullback-Leibler(KL)散度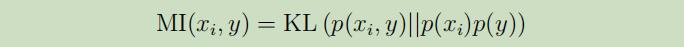： 它为我们提供了一种评估概率分布$p(x_{i}, y)$ 和$p(x_{i}) p(y)$之间差异程度的方法。如果$x_i$和y都是独立随机变量，然后我们可以有$p(x_{i}, y)=p(x_{i}) p(y$，这时这两个分布的KL-散度将为0。这与“如果$x_i$和y是独立的，那么$x_i$对于y是无信息交互”这个思想是一致的，因此分数$S(i)$将会很小。

最后一个细节： 现在你可以根据特征的分数$S(i)$来对特征进行评级，但是你怎么决定你需要选择多少特征呢？一个标准的做法是使用交叉验证来选择可能的k值。例如当使用朴素贝叶斯来进行文本分类（词汇表大小通常非常大），使用这种方法来选择出的特征子集经常会提升分类器的精准性。

贝叶斯统计和正则化（Bayesian statistcs and regularization）

在这一章节，我们将介绍一些工具来一定程度的解决过拟合问题。

在最开始的几节课中，我们就讨论过使用极大似然（maximun likehood）来拟合我们的参数，并根据如下公式来选择我们的参数：在之后的讨论中我们可以把θ看作为未知的参数。频率统计学家的观点认为θ是常量但未知，它不是随机的，并且我们的工作就是要通过统计的手段（例如极大似然）来估计出这个参数的值。

但是贝叶斯 的观点认为θ是一个值未知的随机变量，在他提出的这种方法中，我们首先要明确一个关于参数θ的先验概率 $p(θ)$来表达出我们关于这个参数的先验认知的预测。然后给定训练集$S=\lbrace (x^{(i)}, y^{(i)})\rbrace_ {i=1}^m$ ，当我们要对新的输入x做出预测时，我们可以计算其后验概率分布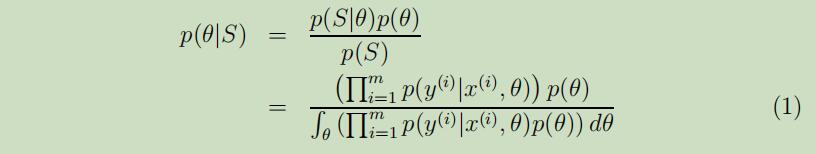： 在上面你的等式中，$p(y^{(i)} | x^{(i)}, \theta)$从你针对学习问题所使用的模型里产生。例如对于贝叶斯逻辑回归，你可能选择$p(y^{(i)} | x^{(i)}, \theta)=h_ {\theta}(x^{(i)})^{y^{(i)}}(1-h_ {\theta}(x^{(i)}))^{(1-y^{(i)})}$，其中$h_ {\theta}(x^{(i)})=1 /(1+\exp (-\theta^{T} x^{(i)}))^{3}$。

当我们被给定新的输入x，并且要做预测时，我们可以计算使用了θ后验概率的分类标签的后验概率：

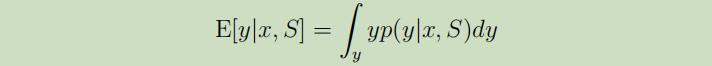
在上面的这个等式中，$p(\theta | S)$来自于等式（1）。因此我们可以将y输出为： 如果y是离散的，那么积分可以被替换成累加 如上我们所讲述的贝叶斯预测流程可以被看作为做了一次“全贝叶斯”预测，其中我们的预测是通过对参数θ的后验概率取均值（期望）来计算的。不幸的是，通常计算这个后验概率分布在计算上非常困难，因为这需要在等式（1）中对高维的θ进行积分。

因此，在实际中我们并不使用θ的后验分布估计，通常的做法为将等式（2）中的θ后验分布替换为一个单独的点估计。θ的MAP(maximum a posteriori)估计为：

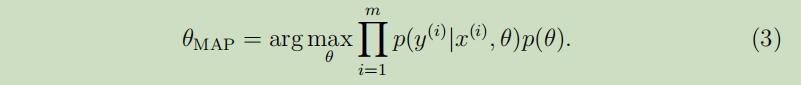
可以注意到，这个公式除了在最后有了个先验概率$p(\theta)$外，和参数θ的极大似然公式十分相似。

在实际的应用中，对于先验分布$p(\theta)$的选择通常为假设其服从$\theta \sim \mathcal{N}(0, \tau^{2} I)$。通过这个选择你和的参数$\theta_{\mathrm{MAP}}$将会比选择极大似然方法有更小的范数，并且更不易造成参数的过拟合（如下图所示，τ的值越小，其预测出的曲线会更光滑）。

正则化

转载自https://www.cnblogs.com/llhthinker/p/5351201.html

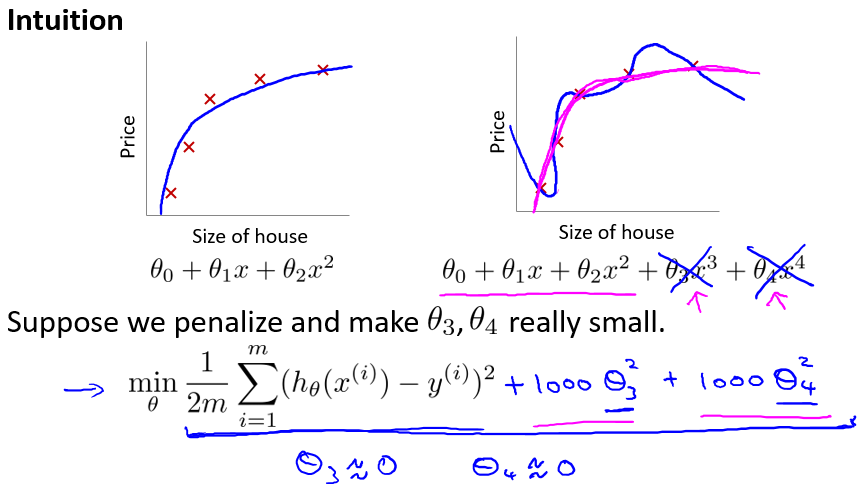
下面说明如何利用正则化来完善cost function. 首先看一个直观的例子。如下图所示，一开始由于多项式次数过高导致过拟合，但是如果在cost function后加上$1000\theta_3^2+1000\theta_4^2$, 为了使cost function最小，那么在优化(迭代)过程中，会使得theta3和theta4趋近于0，这样多项式后两项的高次作用就减少，过拟合得到了改善。这就相当于对非一般化特征量的惩罚。

Regularized linear regression

一般的，对于线性模型正则化后的cost function如下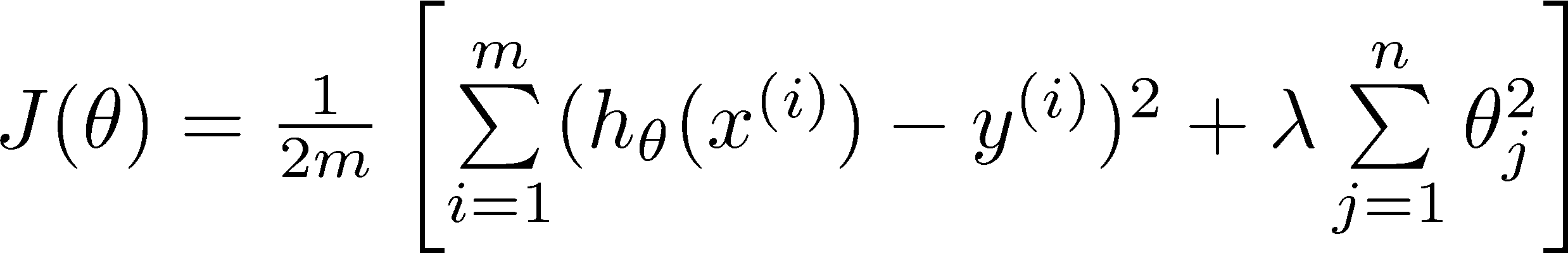：（注意正则化不包括theta0） Lambda的取值应该合适，如果过大(如10^10)将会导致theta都趋于0，所有的特征量没有被学习到，导致欠拟合。后面将会讨论lambda的取值，现在暂时认为在0~10之间。

既然cost function改变了，那么如果采用梯度下降法来优化，自然也要做相应的改变，如下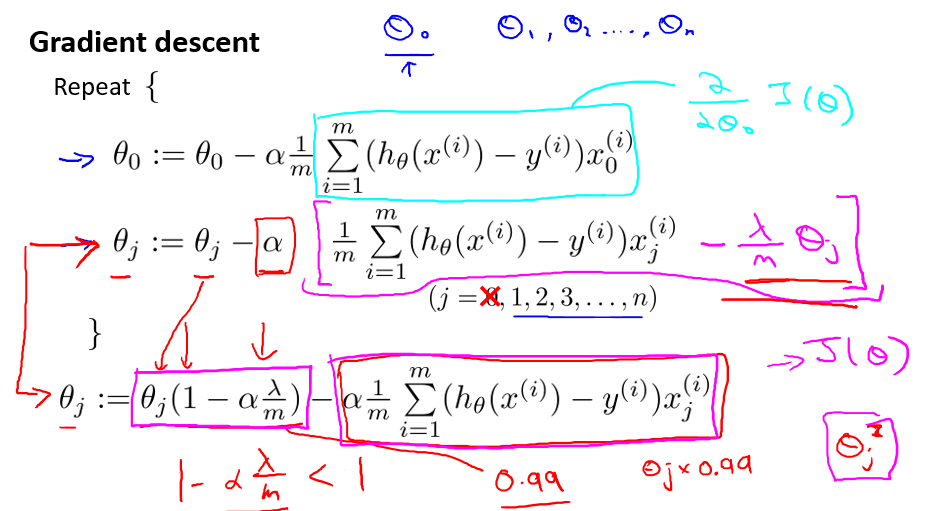：作为线性回归的另一种模型，正规方程(the normal equations)也可以正则化，方式如下：我们知道，如果训练样本数m小于等于特征数n，那么X’X是不可逆的(使用matlab中pinv可以得到其伪逆)，但是如果lambda > 0，则加上lambda乘以上图形式的矩阵后就可逆了。

吴恩达Stanford机器学习公开课（十）笔记