网易公开课视频地址：http://open.163.com/movie/2008/1/U/O/M6SGF6VB4_M6SGJURUO.html 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes6.pdf 和https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/ML-advice.pdf
Lecture 11 - Online learning, Advice for applying Machine Learning
Online Learining
在线学习方式是在学习算法在学习的过程中，边学习边预测。
在这样的设定下，假设学习算法被给定一系列的训练样本$(x^{(1)}, y^{(1)}),(x^{(2)}, y^{(2)}), \ldots(x^{(m)}, y^{(m)})$，首先给定算法$x^{(1)}$,让算法来估计$y^{(1)}$的值，随后在向算法揭露出真正的$y^{(1)}$值；然后给定$x^{(2)}$，估计$y^{(2)}$，揭露$y^{(2)}$，并依次类推..
在在线学习过程中，我们最需要注意的是算法整个运行过程中的总体误差数,下面我们将使用感知器算法为例子来对在线学习方式的误差做一个约束界限。为了方便导出之后的公式，我们将约定分类标签为$y \in {-1,1}$。
在我们的感知器算法中有参数$\theta \in \mathbb{R}^{n+1}$,它根据公式（1）来做出预测：
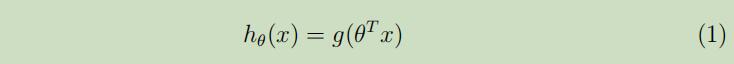其中
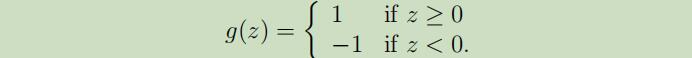
当给定训练样本$(x, y)$，感知器算法的参数更新规则如下：若$h_{\theta}(x)=y$，则不对参数θ做任何改动；否则，对参数θ做如下更新：
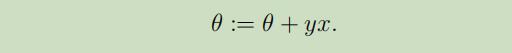
下面让我们引出一个定理，这个定理可以对使用在线学习方式的感知器算法每次更新时的误差给定一个界限。注意下面对误差数的界限约束并没有明显的依赖于样本数m和输入x的维度n。
定理（Block,1962,and Novikoff,1962）： 给定样本$(x^{(1)}, y^{(1)}),(x^{(2)}, y^{(2)}), \ldots(x^{(m)}, y^{(m)})$，假设对于所有的i都有$|x^{(i)}| \leq D$，并且存在单位向量u满足$y^{(i)} \cdot(u^{T} x^{(i)}) \geq \gamma$（如果$y^{(i)}=1$，则$u^{T} x^{(i)} \geq \gamma$；如果$y^{(i)}=-1$，则$u^{T} x^{(i)} \leq-\gamma$。这样u就可以把数据分离成边距至少为γ的两半）。这时，感知器算法总共预测出错的个数最多为$(D / \gamma)^{2}$。
定理证明：感知器算法只会对预测出了问题的样本更新其权值，另$\theta^{(k)}$它做第k次错误预测时使用的权值，所以当$\theta^{(1)}=\overrightarrow{0}$时，如果对该训练集来说存在第k的预测错误，则会有$g((x^{(i)})^{T} \theta^{(k)}) \neq y^{(i)}$，由此可以推出：
同时，从感知器算法的学习规则中，我们也可以得知$\theta^{(k+1)}=\theta^{(k)}+y^{(i)} x^{(i)}$.对其两边同乘单位向量u可以得到：
在根据数学归纳法可以得到：
我们对更新公式两边同时求模，可以得到：
第三步使用了等式（2）。再次根据数学归纳法可以得到：
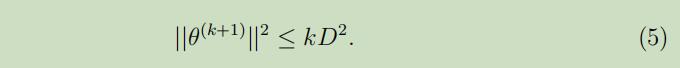
将（3）和（5）合并可以得到：
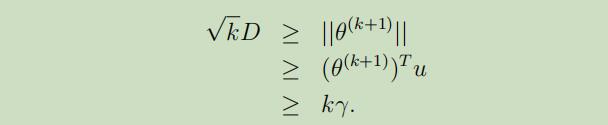其中的第二步是因为
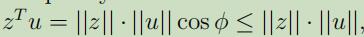
所以就可以得出我们的结果$k \leq(D / \gamma)^{2}$。
Advice for applying Machine Learning
在这一部分，我们主要讨论如下几个论点：
- 为调试学习算法过程中出现的错误做诊断
- 误差分析和销蚀分析
- 如果从一个机器学习问题开始着手
对学习算法的调试
启发式例子： 反垃圾邮件系统。
- 你精心挑选了100个单做来当做特征（而不是使用英语词汇表中所有的单词）
- 用贝叶斯逻辑回归来建模，并使用梯度下降算法。
- 最后你得到了20%的训练误差，这误差太高了！不可以接受！
- 然后你该怎么做呢？
几种常用的调试方法：尝试通过不同的方式来提升算法。
- 尝试使用更多的训练样本
- 尝试使用更小的特征集合
- 尝试使用更大的特征集合
- 尝试改变特征集合的构成：邮件标题或者邮件主体的特征
- 进行更多次的梯度迭代
- 尝试更换为牛顿方法
- 使用不同的λ值
- 尝试使用SVM建模
这些调试方法可能是能够起作用的，但是全部检查一遍这就太过于耗时了，并且还需要有足够的运气才能最终修复出现的问题。
诊断是偏差还是方差的问题
如例子所说，使用贝叶斯逻辑回归的测试误差率为20%。
现在我们就需要来找出是什么原因导致了那么高的误差率。 现在假设造成这种问题的原因有两种：
- 过拟合（高方差）
- 太少的特征（高偏差）
现在为了区分到底是高方差还是高偏差造成的问题，我们首先来看下典型的高方差学习曲线：
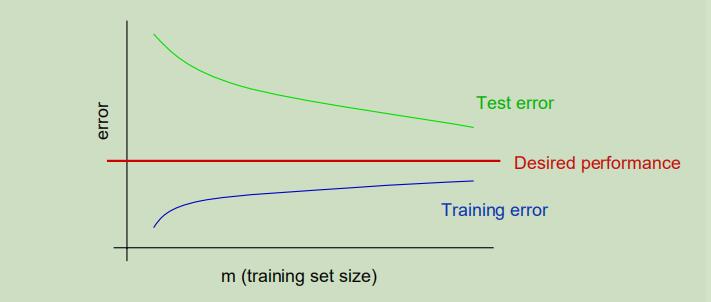特点如下：
- 测试误差随着训练集的增大而减小
- 训练误差和测试误差中间会有很大的空隙
典型的高偏差学习曲线：
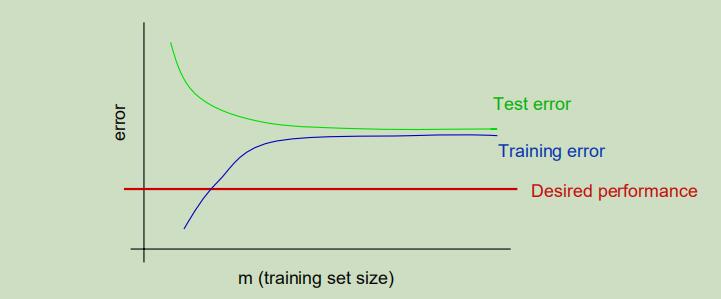特点如下：
- 训练误差会出奇的高
- 训练误差和测试误差之间仅有很小的空隙
因此，对于此问题我们的诊断手段如下：
- 高方差：训练误差将会比测试误差低非常的多
- 高偏差：训练误差同样会很高
对于上述方法来说，以下做法可以相应的解决：
- 尝试使用更多的训练样本 （修复高方差问题）
- 尝试使用更小的特征集合 （修复高方差问题）
- 尝试使用更大的特征集合 （修复高偏差问题）
- 尝试改变特征集合的构成：邮件标题或者邮件主体的特征 （修复高偏差问题）
其他诊断手段
偏差以及方差问题是一种常用的诊断手段，但是对于其他的问题们，通常需要利用你自己的聪明才智来构建自己的诊断方法来指出哪里出了问题。
另一个例子：
- 使用贝叶斯逻辑回归，对垃圾邮件判断有2%的误差，对非垃圾邮件的判断同样有2%的误差（这对实际应用来说是过于高的）
- 使用线性核的SVM算法，对垃圾邮件判断有10%的误差，对非垃圾邮件的判断有0.01%的误差（可以接受的比例）
- 但是为了计算的高校性，你仍然想要使用逻辑回归。
- 接着你需要怎么做？
现在让我们来关注机器学习领域中另一个常见问题：
你确定你的算法（逻辑回归中的梯度下降）收敛了吗？
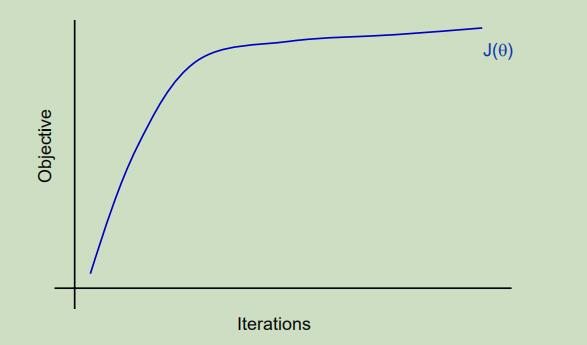
通常很难从目标函数中来看出来算法是否已经收敛
其他同样常见的问题还有：
- 是否选择了正确的优化函数？例如你目前所关心的为：
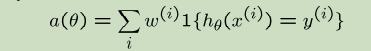
- 采用贝叶斯逻辑回归是否适用？λ选择了正确的值？
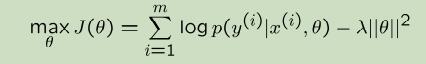
- 采用SVM是否适用？C选择了正确的值？
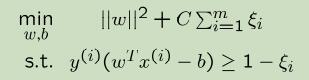
尽管SVM的的结果比贝叶斯逻辑回归好，但是你十分想用贝贝叶斯逻辑回归来部署你的应用。
现在令$θ_{SVM}$为通过SVM学习获得的参数，令$θ_{BLR}$为通过贝叶斯逻辑回归学习得到的参数
你关心的加权准确率函数如下：
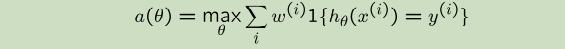
因为$θ_{SVM}$比$θ_{BLR}$的性能更好，所以
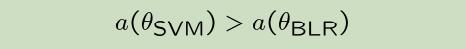
贝叶斯逻辑回归要做的是尝试最大化
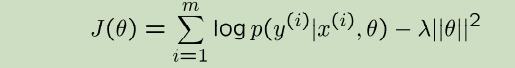
我们所需的诊断工作为判断：
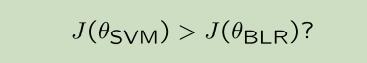
考虑如下两个案例：
Case 1：
在这种情况下：贝叶斯逻辑回归的任务就是要最大化J(θ)，出现这种情况就意味着参数$θ_{BLR}$并没有能够使J(θ)最大化，问题可能出到了算法有没有收敛的身上。因此这种情况是优化算法的问题。
Case 2：
这种情况表明了贝叶斯逻辑回归成功的最大化了J(θ)，但是SVM虽然在J(θ)表现得不好，却实际上有更高的加权精准率a(θ)。
这通常意味着你所最大化的J(θ)是个错误的目标函数，问题出在了目标函数的选择上了。
对于上述方法来说，以下做法可以相应的解决：
- 对梯度下降进行更多次的迭代 （修复优化算法的问题）
- 尝试更换为牛顿方法 （修复优化算法的问题）
- 使用不同的λ值 （修复优化目标函数的问题）
- 尝试使用SVM建模 （修复优化目标函数的问题）
实际应用的调试案例
以斯坦福的无人驾驶直升机为例子，对此问题建模过程如下：
- 搭建一个直升机仿真环境
- 选择一个损失函数，例如$J(\theta)=|x-x_{\text { desired }}|^{2}$ x为直升机坐标
- 让直升机运用强化学习算法在仿真环境中运行，所以我们要尝试去最小化损失函数
假设当我们完成了上面的步骤之后，发现参数$\theta_{\mathrm{RL}}$控制的直升机比驾驶员差太多了。之后该怎么做呢？
- 提升仿真器的仿真程度？
- 修改损失函数J？
- 修改强化学习算法？
下面来让我们进行如下的假设：
- 假设直升机的仿真环境是准确无误的。
- 假设可以通过最小化J(θ)来使强化学习算法准确的在仿真环境中控制直升机。
- 假设最小化J(θ)就等同于自动驾驶的正确化程度 然后通过这种方法学习获得的采纳数$\theta_{\mathrm{RL}}$能够很好的应用在真实的直升机上。
具体的诊断方法：
- 如果参数$\theta_{\mathrm{RL}}$在仿真环境中运作的很好，但是在真实环境中就不行。那么问题就出现在了仿真环境上了。
- 令$\theta_{\text { human }}$代表人类的控制策略。如果$\mathrm{f}(\theta_{\text { human }})<\mathrm{J}(\theta_{\mathrm{RL}})$，那么问题就出现在了强化学习算法上了（因为没有能够最小化损失函数J）
- 如果$J(\theta_{\text { human }}) \geq J(\theta_{\mathrm{RL}})$，那么问题就出在了损失函数的身上（最小化损失函数不等同于能够有很好的飞行策略）
对于诊断分析更多的建议：
- 通常，你需要自己去思考制定一种属于自己的诊断方法来解决算法中的错误。
- 即使你的学习算法运行的很好， 你最好还是能够对你的算法进行一次诊断，来确保你真正的理解算法的运行状况。这对于以下情况十分有用： 2.1 理解应用中出现的问题：如果你的工作负责一个十分重要的ML应用在之后的一大段时间里，对你个人来说能够培养出你的一种直觉来更好的理解问题中运行好和不好的地方。 2.2 写研究论文：诊断措施和错误分析可以帮助你替身对问题的洞察力，并且用来证明你的研究申明是正确的。
误差分析（Error analysis）
假设你的人脸识别系统包括如下模块，那你该怎么来确定是哪一个模块造成的误差呢？
现在我们依次的对每个模块提供精准的数据集，来看性能提升的程度
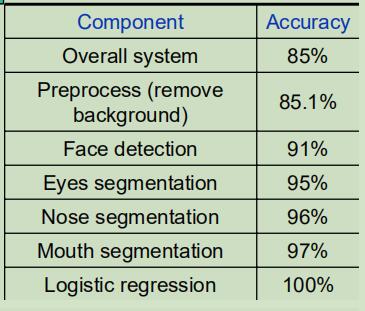可以总结出，预处理能带来的性能提升空间很小，但是面部识别和眼睛分割还有很大的空间可以提升。
销蚀分析（Ablative 分析）
假设对图片直接使用逻辑回归可以得到94%的性能，但是全部的系统可以获得99.9%的性能，所以你想知道是什么部分导致的巨大的提升呢？
每次从你的系统中移除一个元件，观察变化：
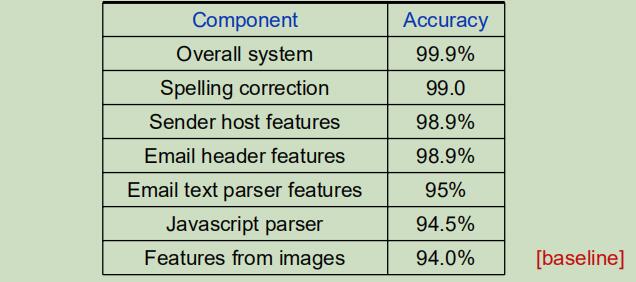结论：邮件文本解析可以带来最大的性能提升。
总而言之，误差分析可以解释当前性能与完美性能之间为什么存在不同？ 销蚀分析可以解释一些更差的性能和当前性能之间为什么存在不同？
着手开始一个机器学习问题
方法1：细心的设计
- 花很长的时间用来精心设计争取的特征值，手机正确的数据集，设计正确的算法结构
- 目的：产生新的学习算法，更好、更具扩展性的算法。
方法2：build-and-fix：
- 先实现一个快速但简陋的模型
- 对其使用误差分析和斩断手段，来修复其中的错误
- 目的：快速解决一个问题，并投入市场中。
注意： 不要过早的优化，使用误差分析先来决定那一模块需要重点设计，并少设计与任务关系不密切的模块。
