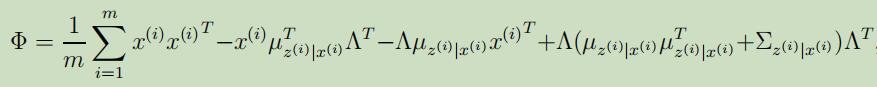网易公开课视频地址：http://open.163.com/movie/2008/1/L/3/M6SGF6VB4_M6SGKK6L3.html 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes9.pdf
Lecture 13 - Factor analysis
当我们拥有来自许多高斯分布混合着的数据$x^{(i)} \in \mathbb{R}^{n}$，EM算法可以用来拟合一个混合模型。在这种设定下，我们通常设想我们的问题具有足够多的的数据来分辨出数据的多高斯结构，例如，训练集大小m远远大于数据的维度n。
但是，现在让我们来考虑当$n \gg m$的情况，因为m个数据点仅仅覆盖$\mathbb{R}^{n}$很小维度的子空间，所以在这类问题中，对这些数据甚至建立一个单高斯模型都会很困难。如果我们，将这些数据用高斯分布建模，并使用极大似然估计来估计出期望和协方差，
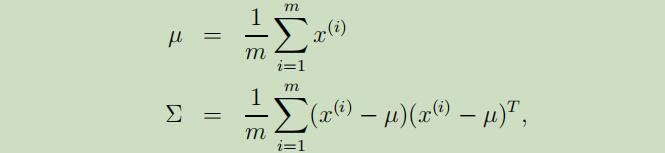但是我们会发现得到的协方差矩阵$\Sigma$是奇异的（为什么？待解决），这就意味着$\Sigma$的行列式等于0，不可求逆。这就造成了多元高斯分布的不可解问题，如下图：
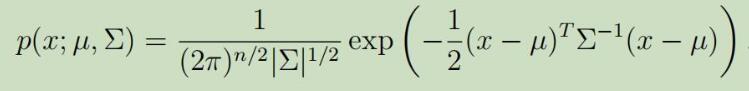
更一般地，除非在m超过n并超过一定的程度下，否则关于期望和协方差的极大似然估计的质量将会相当的低。但是尽管如此，我们仍然可以对这些稀少的数据建立一个合理的高斯模型，并且可以从数据中捕获出有意思的协方差结构。
1. 重新对$\Sigma$进行约束
如果我们没有足够的数据来拟合一个满秩的协方差矩阵，那么我们可以对$\Sigma$加以约束。例如，我们可以选择去拟合一个协方差对角矩阵，其极大似然估计如下：
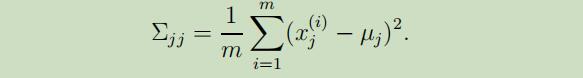可以看出来，$\sum_{j j}$就简单的是数据的第j个坐标上变动着的经验估计。
有时，我们还可以对$\Sigma$进一步加以约束，令它的对角线上所有的元素值都相等。例如，我们可以领$\Sigma=\sigma^{2} I$，其中$\sigma^{2}$是我们可以控制的参数，它的极大似然估计如下：
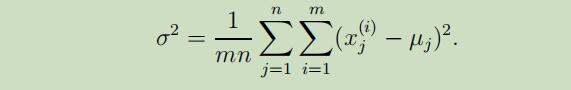
这样拟合出来的高斯模型的密度函数将为圆形、球形或超球体
在上面任一一个约束下，我们可以得到当$m \geq 2$时的非奇异矩阵$\Sigma$。然而，为了保证其为对角矩阵，就意味着需要数据中不同坐标下的$x_{i}, x_{j}$是相互独立或不相关的，这样才能使协方差矩阵的其他区域为0。但是仅使用上面的这两个约束并不能捕获数据中的一些结构，所以我们接下来需要描述因子分析模型，不需要拟合一个满秩的协方差矩阵就可以捕获一些有趣的结构。
2. 多元高斯分布的边缘及条件分布
假设我们有基于向量的随机变量
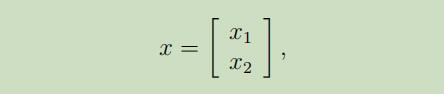其中$x_{1} \in \mathbb{R}^{r}, x_{2} \in \mathbb{R}^{s},$ 且$x \in \mathbb{R}^{r+s}$。假设$x \sim \mathcal{N}(\mu, \Sigma)$，参数为
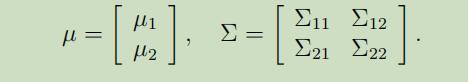其中$\mu_{1} \in \mathbb{R}^{r}, \mu_{2} \in \mathbb{R}^{s}, \Sigma_{11} \in \mathbb{R}^{r \times r}, \Sigma_{12} \in \mathbb{R}^{r \times s}$。因为协方差矩阵是对称的，所以有$\Sigma_{12}=\Sigma_{21}^{T}$。
在我们的假设下，$x_{1}$和$x_{2}$是联合多元高斯分布，那么$x_{1}$的边缘分布是什么呢？不难得到$\operatorname{Cov}(x_{1})=\mathrm{E}[(x_{1}-\mu_{1})(x_{1}-\mu_{1})^T]=\Sigma_{11}$。同样也可以得到
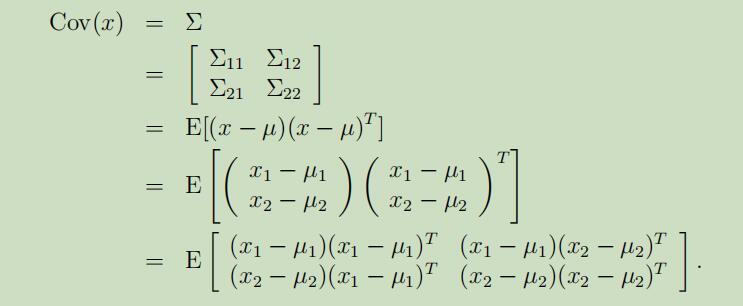
因为这些分布的边缘分布就是他们自己的高斯分布，所以$x_{1}$的边缘分布为$x_{1} \sim \mathcal{N}(\mu_{1}, \Sigma_{11})$。
那么，给定$x_{2}$的情况下，$x_{1}$的条件分布呢？ $x_{1} | x_{2} \sim \mathcal{N}(\mu_{1 | 2}, \Sigma_{1 | 2})$，其中
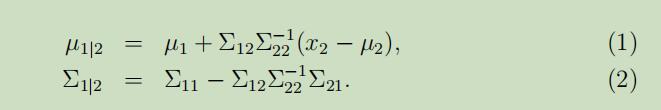
因子分析模型（The Factor analysis model）
在此因子分析模型中，我们假设存在如下的联合分布$(x, z)$，其中$z \in \mathbb{R}^{k}$是潜在随机变量：
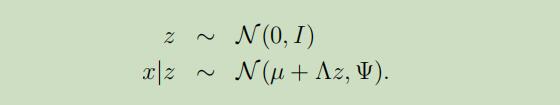此模型的参数有向量$\mu \in \mathbb{R}^{n}$，矩阵$\Lambda \in \mathbb{R}^{n \times k}$和对角矩阵$\Psi \in \mathbb{R}^{n \times n}$。并且k小于n。
因此，我们设想每一个样本点$x^{(i)}$都是通过从k维的多元高斯$z^{(i)}$取样来生成的，然后它通过计算$\mu+\Lambda z^{(i)}$来映射到$\mathbb{R}^{n}$的k维放射空间中。所以，$x^{(i)}$是通过在$z^{(i)}$的基础上增加噪声$\mu+\Lambda z^{(i)}$来实现的。
现在，我们可以将因子分析模型重新定义如下：
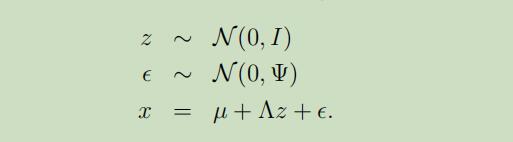
ε和z是独立的
或者说，我们可以把模型更加精准的定义为，联合高斯分布的形式：
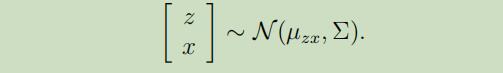
我们接下来要做的就是找出模型中的$\mu_{z x}$和$\Sigma$
且又因为$z \sim \mathcal{N}(0, I)$，所以可以得到
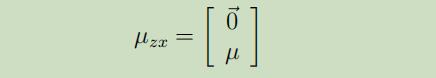
下一步，就是要来寻找$\Sigma$。
所需要计算的子协方差矩阵有$\Sigma_{z z}=\mathrm{E}[(z-\mathrm{E}[z])(z-\mathrm{E}[z])^{T}]$（$\Sigma$的左上角），$\Sigma_{z x}=\mathrm{E}[(z-\mathrm{E}[z])(x-\mathrm{E}[x])^{T}]$（右上角），和$\Sigma_{x x}=\mathrm{E}[(x-\mathrm{E}[x])(x-\mathrm{E}[x])^{T}]$（右下角）
因为$z \sim \mathcal{N}(0, I)$，可以得到$\Sigma_{z z}=\operatorname{Cov}(z)=I$，还有
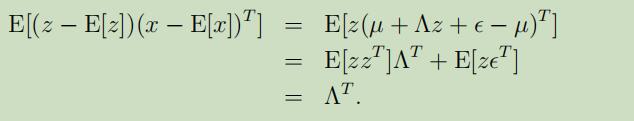在最后一步中，利用了$\mathrm{E}[z z^{T}]=\operatorname{Cov}(z)$和$\mathrm{E}[z \epsilon^{T}]=\mathrm{E}[z] \mathrm{E}[\epsilon^{T}]=0$来推导出。
$\Sigma_{x x}$如下：
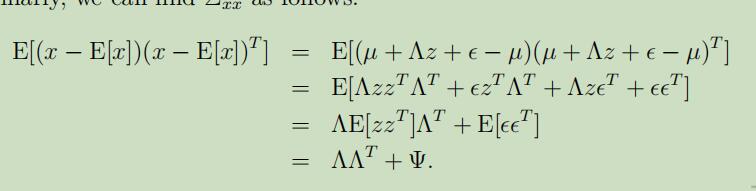
将这些推导出来的拼在一起，可以得到：
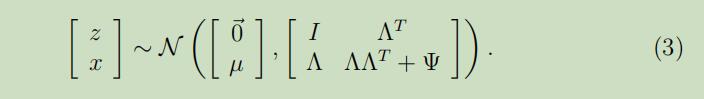
所以，也可以推导出x的边缘分布为$x \sim \mathcal{N}(\mu, \Lambda \Lambda^{T}+\Psi)$
最后，模型的对数似然函数可以被写为：
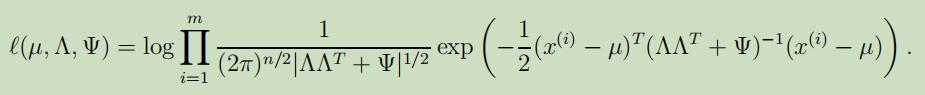
但是，若使用极大似然来将其最大化是困难的，所以，我们需要使用EM算法来代替。
使用EM模型来进行因子分析
E-step的导出过程比较简单，我们需要计算$Q_{i}(z^{(i)})=p(z^{(i)} | x^{(i)} ; \mu, \Lambda, \Psi)$即可。在通过把等式（3）和（1-2）中使用的分布替换为条件高斯分布后，我们可以得到$z^{(i)} | x^{(i)} ; \mu, \Lambda, \Psi \sim \mathcal{N}(\mu_{z^{(i)} | x^{(i)}}, \Sigma_{z^{(i)} | x^{(i)}})$，其中
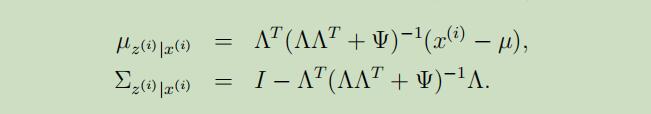
所以根据条件多元高斯模型的定义，我们可以得到
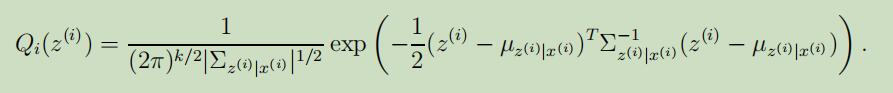
现在让我们来开始导出M-step，我们需要最大化的函数为
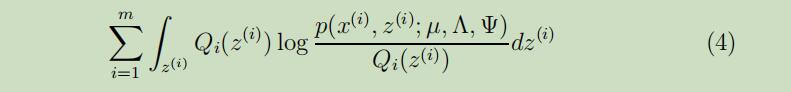
下面我们来展示参数$\Lambda$的极大似然估计的导出过程，参数$\mu,\Psi$的极大似然估计导出过程将在作业中展示。
将公式（4）可以展开为如下：
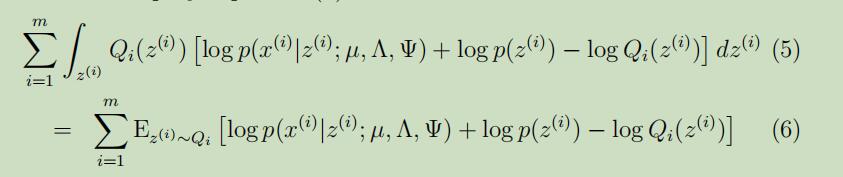
下面的期望会省略期望的下标缩写，在去除掉和参数$\Lambda$无关的项后，我们得到似然函数：
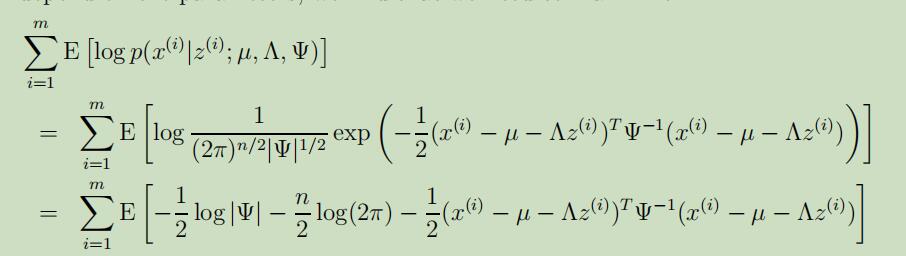
将上式展开后，再把和$\Lambda$无关的项去除后，使其最大化。具体为：对式子关于$\Lambda$求偏导，其中需要利用到$\operatorname{tr} a=a($ for $a \in \mathbb{R})$，$\operatorname{tr} A B=\operatorname{tr} B A$，和$\nabla_{A} \operatorname{tr} A B A^{T} C=C A B+C^{T} A B$等公式，可以得到：
令等于0，并化简后可以得到：
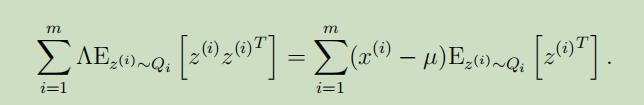
因此，解出$\Lambda$，得：
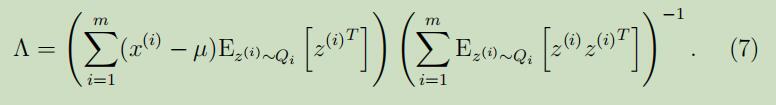
这里很有趣的可以看到，这个等式的导出过程和最小二乘回归的Normal 等式的导出过程联系紧密
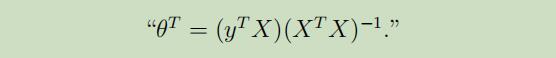这里的$x^{\prime} \mathrm{s}$是$z^{\prime} \mathrm{s}$的线性函数（噪声），当给定E-step中关于z的猜测之后，我们将要去估计这个未知的线性参数$\Lambda$的值，因此，回合normal equation有点像，但是差别在于，最小二乘使用的是关于$z^{\prime} \mathrm{s}$的“最佳猜测”。
为了完成我们的M-step中的更新，需要先计算出等式（7）中涉及的期望。
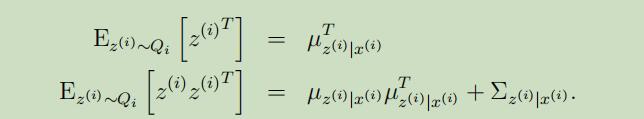其中第二个式子源自于$\operatorname{Cov}(Y)=\mathrm{E}[Y Y^{T}]-\mathrm{E}[Y] \mathrm{E}[Y]^{T}$，所以有$\mathrm{E}[Y Y^{T}]=\mathrm{E}[Y] \mathrm{E}[Y]^{T}+\operatorname{Cov}(Y)$。将其**带入到等式（7）中，可以得到关于$\Lambda$的更新公式为：
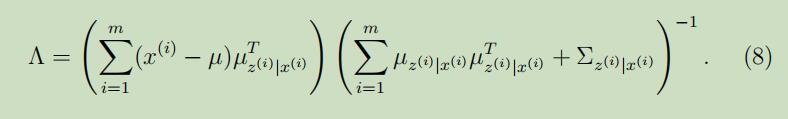
注意到，上式子的右边有$\Sigma_{z^{(i)} | x^{(i)}}$的出现，在导出EM的过程中经常犯的一个错误是，认为仅需要计算$E[z]$。然而例如在建模混合高斯时，我们同时需要计算$E[z z^{T}]$和$\mathrm{E}[z]$。因此，M-step中的更新必须考虑后验分布$p(z^{(i)} | x^{(i)})$中z的协方差。
u的参数更新如下：
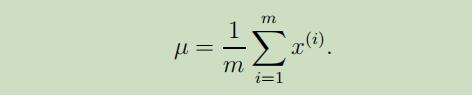
因此这个参数在算法的运行过程中将不再变动，所以只需计算一次即可，不需要反复更新
类似的，对角矩阵$\Psi$可以通过计算如下，且另$\Psi_{i i}=\Phi_{i i}$（$\Psi$仅为$\Phi$对角线上的值）获得：
