视频地址：https://www.bilibili.com/video/av49432977/?p=17 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes12.pdf
Lecture 17 - Continuous state MDPs and Discretization
在此之前，我们的注意力都集中在有限状态的MDP问题中，但现在我们将要讨论无限状态的MDP的算法。例如，对于一辆车，我们可以将它的状态表示为$(x, y, \theta, \dot{x}, \dot{y}, \dot{\theta})$，包括了它的位置$(x,y)$；方向θ；x和y方向上的速度$\dot{x}$和$\dot{y}$；角速度$\dot{θ}$。因此$S=\mathbb{R}^{6}$是一个无限状态集，它有着无限数量的可能的坐标和方向。
在本章节中，我们将考虑在$S=\mathbb{R}^{n}$的设定下，解出MDP得方法。
1. 离散化
也许最简单的方法就是把连续状态的MDP给离散化，然后在使用价值迭代之类的算法求解吧。
其思想可以如下，例如，如果我们有2维的状态$(s_{1}, s_{2})$，我们可以使用网格来离散化状态空间：
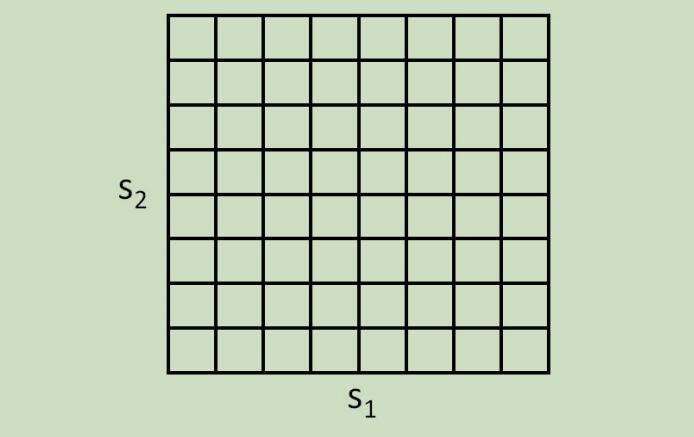
在这里，每一个网格单元都表示一个单独的离散的状态$\overline{s}$，我们可以通过离散的模型属性$(\overline{S}, A,{P_{\overline{s} a}}, \gamma, R)$来估计连续状态的MDP，然后在用相应的迭代算法来求解出$V^{\ast}(\overline{s})$ 和 $\pi^{\ast}(\overline{s})$。
但是，离散化具有两个缺点 。 第一个缺点 ，它假设价值函数在每个离散化的间隔内都是常量（例如，价值函数在上图中的每个网格里为常量）。
为了更好的理解这种表示带来的限制，考虑如下的监督学习问题，怎样为这个数据集拟合出一个函数：
显而易见，线性回归将会很好的完成这个问题。但是如果我们将x轴离散化，然后对离散化的每个间隔内用常量来拟合数据 ，将会出现如下情况：
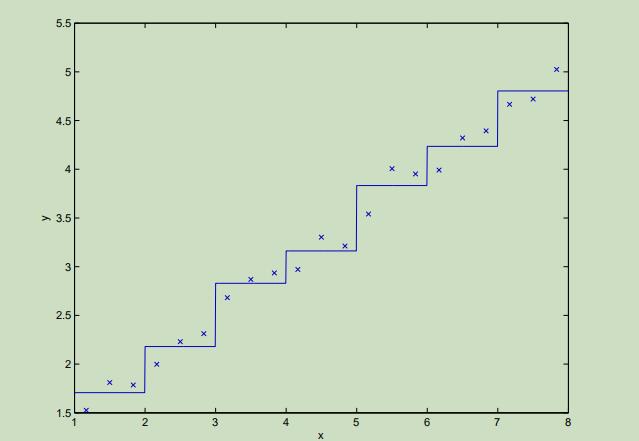
可以看出，这些分段的常量表示并不如哪些光滑的线性函数，这将导致对不同的网格难以泛化。如果需要采用这种离散化的表示方法，我们将需要将这些网格再离散化到非常小，来得到一个好的估计。
第二个缺点，也被称作为维度灾难 ，例如当我们有10维的状态时，如果我们想要将每一维的状态用100个离散化的值来表示，那么我们将会有$100^{10}=10^{20}$个离散的状态，这太…多了，计算机处理不了。
作为经验法则，离散化方法通常在1维或者2维的问题中效果极其的出色，但是选择离散化的方法需要一些机智和谨慎，它通常在最多4维状态的问题中表现不错。如果你极其的聪明，再加上一些运气，也许你甚至能在6维的问题中表现仍然不错。但是，这种方法在更高维度的问题中十分罕见 。
2. 价值函数估计
我们现在将描述另一种方法来在连续状态的MDP中寻找最优的政策 ，它没有使用离散化的思想，而是直接估计$V^{*}$。这种方法称作价值函数估计 ，能够成功地应用于很多RL问题。
2.1 使用一个模型或者仿真器
为了导出价值函数估计算法，我们在之后将要假设我们已经拥有了一个模型或仿真器 。一个仿真器可以是，输入为连续值的状态$s_t$和动作$a_t$，输出为下一个状态$s_{t+1}$(取样自$P_{s_{t} a_{t}}$)：
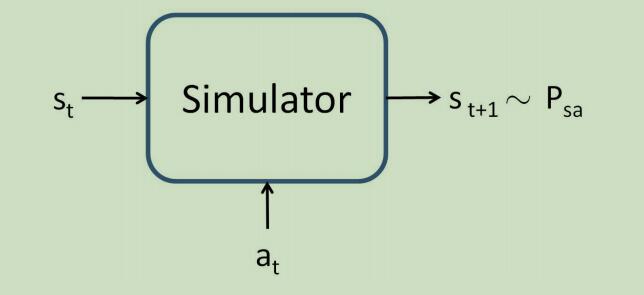
这里由很多种方式来得到这样的一个模型。 第一种方法可以为使用物理模拟仿真器 ，例如可以建造一个模拟钟摆来为我们提供输出。 第二种方法可以为使用现成的物理模拟软件包 ，输入当前的状态$s_t$和动作$a_t$可以计算出对应的系统在接下来很短时间内的状态$s_{t+1}$。
另一种方法通过学习MDP收集到的数据来得到一个模型 ，例如假设我们进行m次实验，每次实验为T个时间步骤，在每个时间点重复且随机的选取动作执行。我们将会观察到如下的m个状态序列：
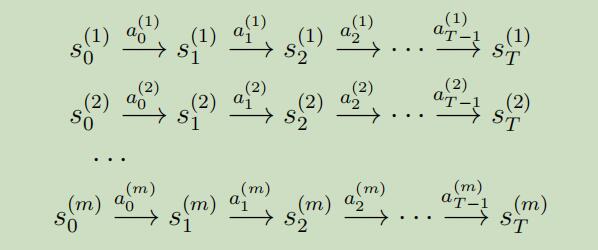
然后，我们可以应用一个学习算法来通过$s_t$和$a_t$预测$s_{t+1}$。例如，一个可能的选择为学习一个如下形式的线性模型 ，这种模型有点类似于线性回归：
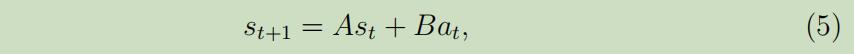这里面模型的参数为矩阵A和B，我们使用从m个实验中收集的数据来估计出它们：
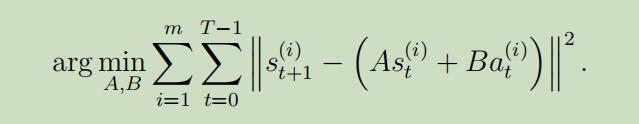
这等同于对这两个参数做极大似然估计
在学习得到参数$A$和$B$后，我们可以选择建立确定性的模型还是建立随机模型 。
在确定性的模型中 ，给定输入$s_t$和$a_t$，根据等式（5）每次输出的$s_{t+1}$是确定的。
在随机模型中 ，输出$s_{t+1}$建模如下：
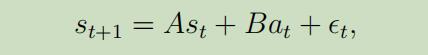其中$\epsilon_{t}$是噪声项，通常被建模为$\epsilon_{t} \sim \mathcal{N}(0, \Sigma)$（协方差可以直接从数据中估计出来）
注意，这里我们将$s_{t+1}$作为当前状态和动作的线性函数 ，但是我们当然也可以建立为一个非线性函数 。比如$s_{t+1}=A \phi_{s}(s_{t})+B \phi_{a}(a_{t})$，其中$\phi_{s}$和$\phi_{a}$是状态和动作的一些非线性特征映射。另外我们也可以选用非线性学习算法，例如局部加权线性回归。这些方法都可以用来为一个MDP建立决定性或随机仿真的模型。
2.2 拟合价值迭代（Fitted value iteration）
我们现在介绍拟合值迭代算法来估计连续状态MDP的价值函数 ，在这后面，我们将假设我们的问题具有连续的状态空间$S=\mathbb{R}^{n}$，但是动作空间A很小且是离散的。
在连续状态MDP下的价值迭代中，我们希望进行如下更新：
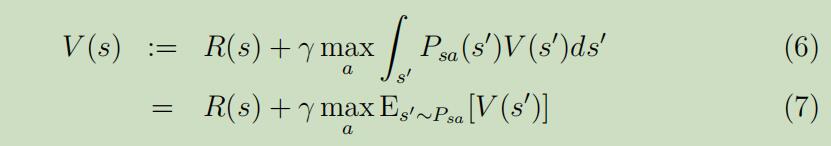
拟合价值迭代的主要思想是：在有限状态的样本$s^{(1)}, \ldots, s^{(m)}$上去使用一种监督学习算法（线性回归）来估计价值函数，它是状态的线性或非线性函数 。
其中$\phi$为状态的一些特征映射。
对于m个状态样本中的每个状态s，拟合价值迭代首先要计算出$R(s)+\gamma \max_a E_{s^{\prime} \sim P_{s a}}[V(s^{\prime})]$（等式7右侧）的估计值$y^{(i)}$，然后应用线性回归来尝试使$V(S)$接近于$y^{(i)}$。
详细的算法如下：
- 随机从S中取样m个状态$s^{(1)}, s^{(2)}, \ldots s^{(m)} \in S$
- 初始化$\theta :=0$
可以从上面的拟合价值迭代算法中看出，它使用线性回归算法尝试使$V(s^{(i)})$ 接近于 $y^{(i)}$。算法的这个步骤和一些标准的回归问题十分相似，只不过把样本x替换为了状态s。虽然我们使用的是线性回归算法，但是其他回归算法（例如局部加权线性回归）也可以被使用。
不同于离散状态下的价值迭代，拟合价值迭代不能被证明总是收敛，然后实际中它通常收敛（或大约收敛），并能很好的应用于很多问题中 。注意，如果我们使用MDP的确定性的模型，那么拟合价值迭代在算法中可以通过设置$k=1$被简化 ，
在最后，拟合价值迭代算法输出$V$，它是$V^{*}$的一种估计，意味着当我们在状态s，需要选择一个动作执行时，我们将选择如下动作：
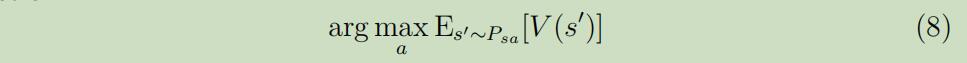这个计算的过程类似于拟合价值迭代算法内层循环中的取样$s_{1}^{\prime}, \ldots, s_{k}^{\prime} \sim P_{s a}$来估计期望这步。
在实际中，通常也有其他方法类估计这步。例如一种非常常用的方法是，仿真器$s_{t+1} = f(s_{t}, a_{t})+\epsilon_{t}$，其中$f$为状态的确定性函数，$\epsilon$为零均值的高斯噪声，然后我们可以选取动作如下：
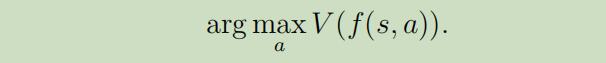
换句话说，我们仅是令$\epsilon_{t}=0$，忽略了仿真器的噪声（因为噪声通常很小，所以是合理的估计），并且设$k=1$。同样的 ，它是从等式（8）中使用估计导出的：
然而，对于一些问题使用这种估计是不正确的，因为它必须要取样$k|A|$个状态来估计上面的期望，计算十分昂贵。
