视频地址：https://www.bilibili.com/video/av49432977/?p=18 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes13.pdf
Lecture 18 - Finite-horizon MDPs，Linear Quadratic Regulation (LQR)
1. Finite-horizon MDPs
在之前的章节中，我们讨论了和定义了MarkovDecision Processes (MDPs)。这本章节中，我们将介绍一种MDP的变体，以便能够处理真实世界中更复杂的任务。
在原先MDP的基础上，作出的改变如下：
-
我们想让我们写出来的公式能够同时表示离散和连续状态的例子，因此，我们将价值函数中的期望计算也成如下形式，不再是累加和积分的形式：
-
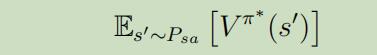
反馈将同时依赖于状态和动作 ，$R : \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$。意味着先前所有的$R(s)$都改变为$R(s,a)$。
-
我们之后将讨论的是有限范围内的MDP，其元组属性被定义为：
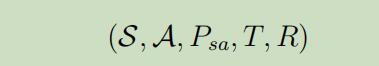其中$T>0$为时间边界（例如$T=100$）。再这样的设定下，我们总共的反馈将会变得些不同：
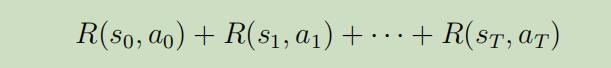而不再是
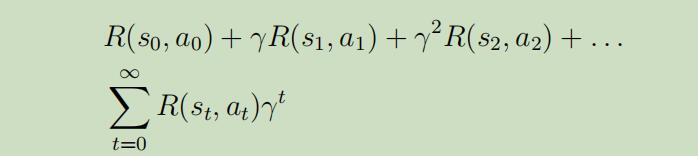
那为什我们移除了折扣因子$γ$呢？ 回忆下当初引入$γ$一部分的原因是确保这种无限累加为有限的，而现在有了$T$加入，总共的反馈本来就成为了有限和，所以折扣因子也没那么大的必要了。
在这样新的设定下，其他的东西也会出现些变化。首先，最优政策$\pi^{*}$可能不在一成不变了，这意味着它将随着时间而改变。
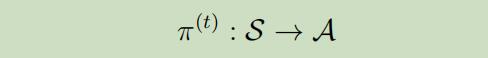其中上标t表示在时间t时的政策。有限边界MDP随着$\pi^{(t)}$的动态流程如下：从状态$s_{0}$开始，在时间点0根据$\pi^{(0)}$采取动作$a_{0} :=\pi^{(0)}\left(s_{0}\right)$，从$P_{s_{0} a_{0}}$取样出下个状态$s_1$，然后再时间1根据$\pi^{(1)}$挑选下个动作$a_{1} :=\pi^{(1)}\left(s_{1}\right)$ 。。。。
为什么在有限边界的设定中是不固定的呢？ 因为我们的策略会受到周围环境和时间的影响。例如，在一个网格中有+1和+10两个目标，刚开始我们可能想让它朝着+10的目标走，但是随着时间的推移，我们剩下的步数不足以到达+10，到足以到+1，所以更好的策略就是朝着+1走。
- 我们的转移概率分布$P_{s_{t}, a_{t}}^{(t)}$也会随着时间而改变，同时还有$R^{(t)}$ ，这样能更贴近现实生活。例如，对一个车来说，油量的剩余、交通的状况都会对转移概率和反馈产生影响。再将前面提出的改变结合起来，我们现在的有限边界MDP的元组属性为
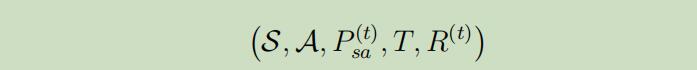
加了时间标签后的价值函数也变为如下形式：
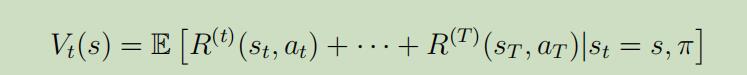
再这样的有限边界的设定下，我们怎么来寻找最优价值函数呢？
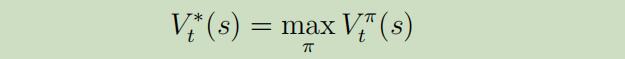
事实证明，可以使用Bellman等式来进行价值迭代，因为Bellman等式可以用来动态规划。那么如何进行价值迭代呢？
-
在最后的那个时间T，最优价值函数为：
-
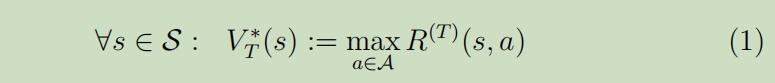
对于时间$0 \leq t<T$内的步骤，我们先假设我们已经知道了下一步的最优价值函数$V_{t+1}^{*}$，然后我们可以得到：
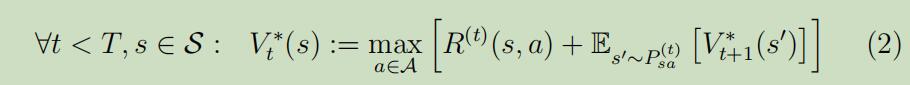
然会我们就可以从T，T-1，T-2…1，依次得出所有时间点对于所有状态的价值函数。
Side note 如果我们把标准的价值迭代运行T步，我们将得到最优价值迭代的$\gamma^{T}$倍估计量（几何收敛）。作业4中见如下定理的证明：
定理 令B表示Bellman更新，$|f(x)|_ {\infty} :=\sup_{x}|f(x)|$。如果$V_{t}$表示第t步的价值函数，那么得到
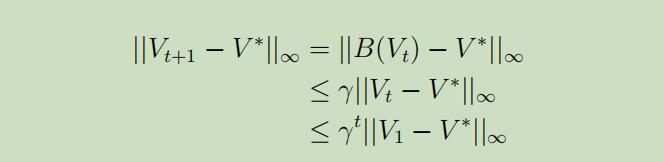
换句话说，Bellman操作B为一个$γ$阶缩小的操作。
2. 线性二次规划(Linear Quadratic Regulation–LQR)
在这部分，将会介绍一种有限边界MDP的特例，求其精确的解释较为容易处理的。
首先，假设我们处于连续状态 的设定：
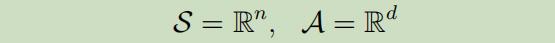
并假设到下一状态的转移是线性关系的
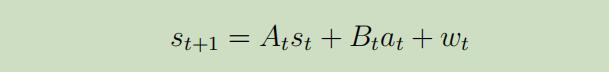其中$A_{t} \in R^{n \times n}$$B_{t} \in R^{n \times d}$是矩阵，$w_{t} \sim \mathcal{N}\left(0, \Sigma_{t}\right)$为服从0均值的高斯噪声。
其实只要均值为0，噪声将不会影响到最优政策
同样假设二次反馈 为：
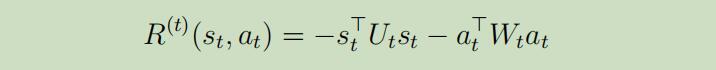其中$U_{t} \in R^{n \times n}, W_{t} \in R^{d \times d}$都为正定矩阵（这就意味着反馈将一直为负值）
Remark： 这里我们将反馈写成二次函数的形式等同我们想让我们的状态接近于原来的状态。例如，当$U_t$和$W_t$都为单位矩阵时，$R_{t}=-\left|s_{t}\right|^{2}-\left|a_{t}\right|^{2}$，这意味着我们想要采取些更平滑些的动作，避免些较大的改变。
在我们定义完成LQR模型后，下面介绍LQR算法的两个步骤：
步骤1： 假设我们不知道矩阵$A, B, \Sigma$的话，就我们需要像以前一样从数据中来学习出它们，使用线性回归来学习参数$A, B \sum_{i=1}^{m} \sum_{t=0}^{T-1}\left|s_{t+1}^{(i)}-\left(A s_{t}^{(i)}+B a_{t}^{(i)}\right)\right|^{2}$，使用高斯判别分析来学习$\Sigma$。
步骤2： 在学习得到模型的参数后，可以使用动态规划来导出最优的政策。
比如说，
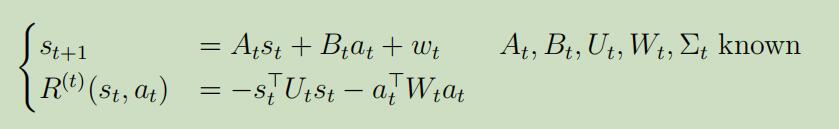
然会使用动态规划来计算$V_{t}^{*}$：
-
初始化步骤 对于，最后的一个时间步T有
-
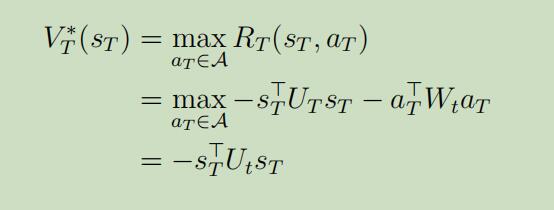
递归步骤 令$t<T$，且已知$V_{t+1}^{*}$。
事实1： 如果$V_{t+1}^{\ast}$是关于$s_t$的二次函数，那么$V_{t}^{\ast}$也是二次函数。换句话说，存在着些矩阵$\Phi$和实数$\Psi$有
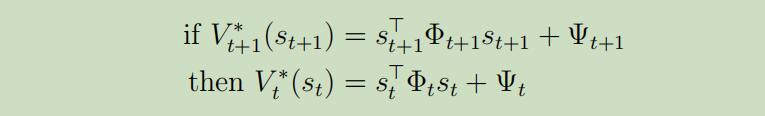当$t=T$时，有$\Phi_{t}=-U_{T}$ 和 $\Psi_{T}=0$。
事实2： 最优政策其实就是状态的一个线性函数。
因为知道了$V_{t+1}^{*}$就等同于知道了$\Phi_{t+1}$ and $\Psi_{t+1}$，所以我们仅需要来解释，如何从$\Phi_{t+1}$ and $\Psi_{t+1}$中计算出$\Phi_{t}$ and $\Psi_{t}$和其他参数:
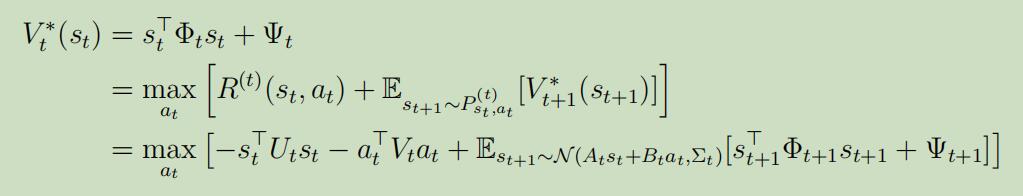
又因为可以很明显的看出来这是关于$a_t$的二次函数，所以我们只需要求导就可以得到最优的动作$a_{t}^{*}$：
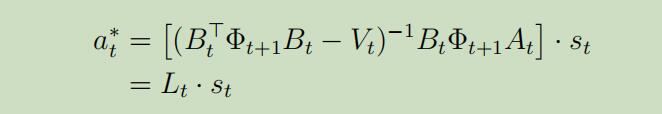
其中
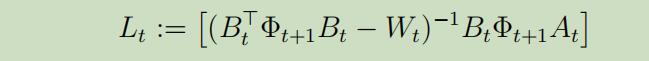
这里我们将得到一个惊人的结论：我们的最优政策是$s_t$的线性函数。 当给定$a_{t}^{*}$时，我们可以解出$\Phi_{t}$ and $\Psi_{t}$，所以最后我们可以得到如下Discrete Ricatti等式 ：
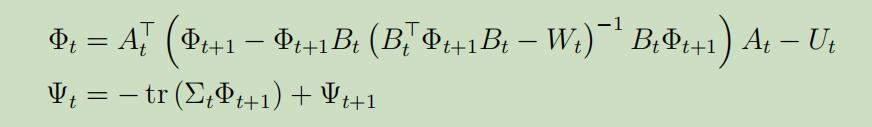
事实3： 从上式可以观察到$\Phi_{t}$既不依赖于$\Psi$也不依赖于噪声$\Sigma_{t}$！ 正如$L_t$是关于$A_{t}, B_{t}$ and $\Phi_{t+1}$的函数，这意味着最优政策也不依赖于噪声！（但是$V_{t}^{*}$依赖于$\Sigma_{t}$）
然后，LQR算法可以总结为如下：
- (如果有必要)估计参数$A_{t}, B_{t}, \Sigma_{t}$
- 初始化$\Phi_{T} :=-U_{T}$和$\Psi_{T} :=0$
- 从$t=T-1 \ldots 0$开始迭代，使用$\Phi_{t+1}$ and $\Psi_{t+1}$来更新$\Phi_{t}$ and $\Psi_{t}$。如果存在一个政策驱使状态朝向0，那么可以证明收敛！
Remark： 使用事实3，我们可以来加速我们的算法。因为最优的政策不依赖于$\Psi_{t}$ ，且$\Phi_{t}$的更新仅依赖于$\Phi_{t+1}$，所以我们可以只更新$\Phi_{t}$！
