视频地址：https://www.bilibili.com/video/av49432977/?p=19 课程主页地址：http://cs229.stanford.edu/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/cs229-notes13.pdf
Lecture 19 - From non-linear dynamics to LQR，Linear Quadratic Gaussian (LQG)
1. From non-linear dynamics to LQR
事实证明，有很多的问题都可以被归结为LQR问题，即使其中的动力系统是非线性的，但是距离普遍应用仍然具有很长的距离。例如反转摆问题，它的状态转移过程为：
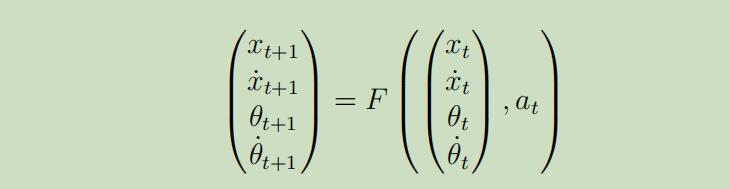
那么，我们能线性化这个系统吗？
1.1 动力系统的线性化
假设将上面的问题描绘如下：
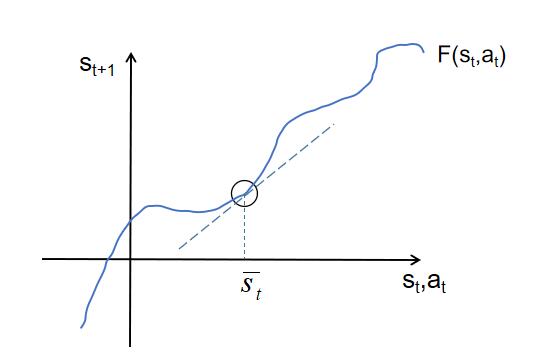其中$\overline{s}_t$和 $\overline{a}_t$为在时间t大约处于的状态和动作，我们使用泰勒展开式来线性化动力曲线，如图中的切线所示，在邻域范围内，可以用切线来代替原来的曲线 。我们先假设状态转移函数F仅依赖于一维的状态s，我们将得到如下，函数$F(s_t)$在$s_t ->\overline{s}_t $时的展开公式：
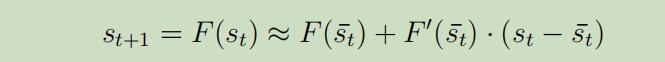
在函数F同时一带与动作时，上面的展开式就可以写为：
现在，$s_{t+1}$就是$s_t$和$a_t$的线性函数，因为我们可以将等式（3）重写为如下形式：
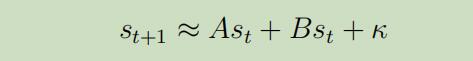其中$\kappa$是常量，A和B是矩阵。现在，就可LQR模型中做的假设一致了。
1.2 微分动力规划（Differential Dynamic Programming (DDP)）
前面介绍的方法对于想要保持在某个状态$s^{*}$附近是非常好的，例如倒立摆问题，然而在很多案例中，想实这样的目标将会是更复杂些的。
我们将介绍一种方法来应用于那些必须要跟随一些轨迹的系统，这种方法要将轨迹离散为一些时间步，并使用先前介绍的技术来达到一些间断性的目标。这种方法称之为微分动力规划 ，其主要步骤为：
步骤1： 使用原生控制器先估计出一个我们想要跟随的轨迹。
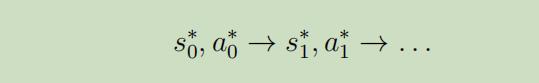
步骤2： 在每个轨迹点$s_{t}^{*}$附近线性化动力系统
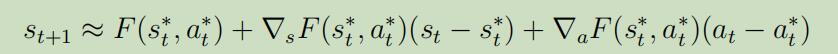其中$s_t,a_t$将会成为我们现在的状态和动作，在我们有了这些每个点的线性估计后，我们可以利用前面的知识来将其重写为：
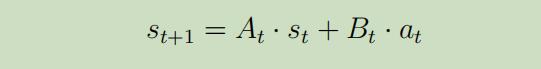
Note： 我们可以对反馈$R^{(t)}$做相似的二阶泰勒扩展处理：
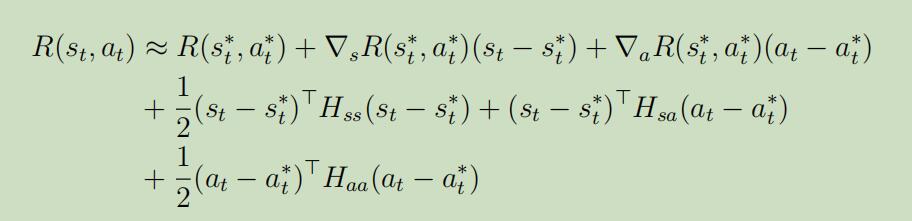可以被重写为：
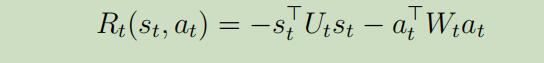
步骤3： 现在，我们目前的问题模型已经严格的被重写为LQR模型框架的形式了，现在让我们使用LQR来寻找最优政策$\pi_{t}$。作为结果，我们新的控制器产生的结果将会越来越棒！
Note： 如果LQR的轨道与线性化估计的轨道差的太远，将会产生很多问题，但是可以通过重塑反馈函数来解决。
步骤4： 现在我们得到了新的控制器（新的政策$\pi_{t}$），我们使用它来产生新的轨迹：
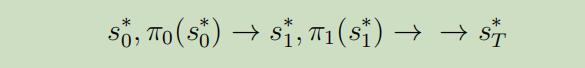
注意当我们生成这个新的轨迹的时候，我们使用真实的函数F而不是线性估计来计算转移的状态，意味着
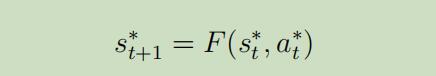然后在返回步骤2，进行重复直到停止。
2. 线性二次高斯（Linear Quadratic Gaussian (LQG)）
在之前介绍MDP的过程中，我们都一直假设我们已知目标的状态，但是在现实世界中，我们可能不能观察到全部的状态$s_t$。例如，飞机的雷达系统可以扫描出敌机的粗略方位，但是并不能得出其所处于的精确状态。因此我们需要一种新的方法来处理这种情况：部分可见的MDPS 。
POMDP是在MDP上增加了一个额外的观察层，所以我们引入了一个新的变量$o_t$，它服从条件分布:
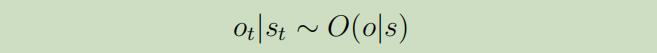
正式的来说，一个有限边界的POMDP具有的元组属性如下：
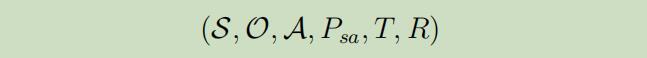再这样的框架下，普遍的策略是，给予我们的观察$o_{1}, \dots, o_{t}$维护一个临时的状态，然后POMDP的一个策略在将这些临时的状态映射到动作。
在本章节中，我们将把LQR扩展到新的设定下。
假设我们观察到$y_{t} \in \mathbb{R}^{m}$如下：
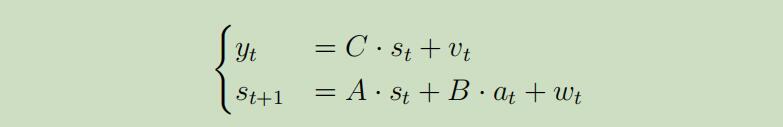其中$m < n$，$C \in R^{m \times n}$是压缩矩阵，$v_t$为传感器噪声（和$w_t$一样服从高斯分布）。反馈函数没有变化，再这样的框架下，寻找最优政策的策略如下：
步骤1： 首先，给予我们所观察到的y，计算出这些临时状态的分布。就是需要计算出如下分布的均值$s_{t | t}$和协方差$\Sigma_{t | t}$：
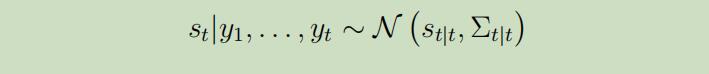
因为协方差矩阵会因为时间而越来越大，计算起来就越来越困难，所以我们将使用Kalman Filter算法来计算
步骤2： 在我们获得上述分布后，我们将使用均值$s_{t | t}$来作为$s_t$的最优估计。
步骤3： 设置动作$a_{t} :=L_{t} s_{t | t}$，其中$L_t$来自于LQR算法
直觉上讲，$s_{t | t}$是$s_t$的估计噪声，但是我们已经证明过了LQR独立于噪声！
为了详细解释步骤1，我们将介绍一个状态转移不依赖于动作的简单的例子，假设：
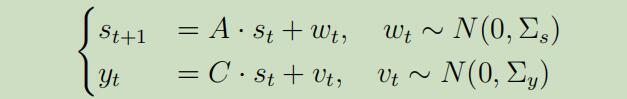
正如噪声都是高斯分布的，我们可以轻松的证明如下联合分布也服从高斯分布：
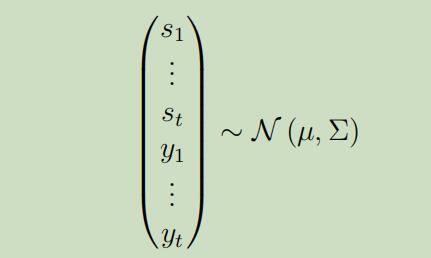
然后使用高斯分布计算边缘分布的公式，可以得到
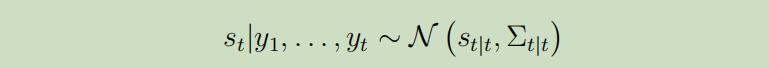
正如之前所说，协方差的计算十分昂贵，我们需要采用Kalman fliter算法 ，它计算这些仅需要$O(t)$的时间，主要基于两个步骤： 首先假设我们已经知道分布$s_{t} | y_{1}, \dots, y_{t}$ 预测步骤 计算$s_{t+1} | y_{1}, \dots, y_{t}$ 更新步骤 计算$s_{t+1} | y_{1}, \dots, y_{t+1}$
在将上述步骤进行多次迭代后，将会更新我们的临时状态，它的流程看起来为：
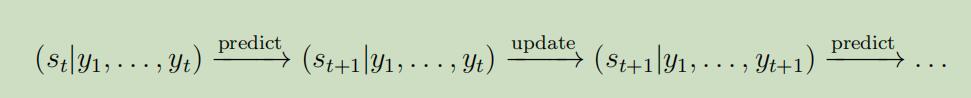
其原理为：
预测步骤： 假设我们已知分布
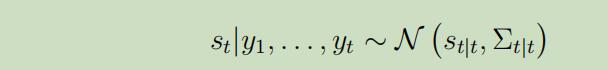
下一个状态的分布也同样服从高斯分布：
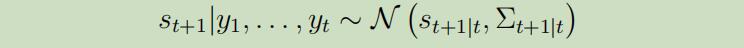其中
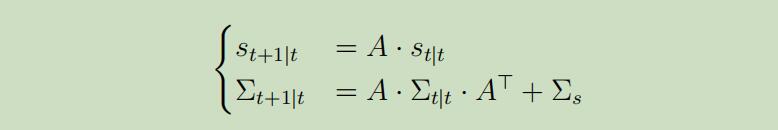
更新步骤： 给定$s_{t+1} | t$和$\Sigma_{t+1 | t}$如下
我们可以证明
其中
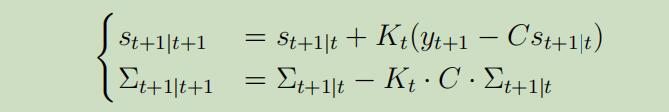
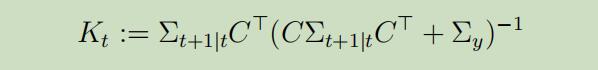
矩阵$K_{t}$称为Kalman gain。
Remark： 如果我们细心的话，我们可以注意到我们并不需要时间t之前的观察！更新步仅依赖于前面的分布，当把上面所有东西放在一起后，算法首先正向计算$K_{t}, \Sigma_{t | t}$ 和 $s_{t | t}$。然后在反向计算这些量$\Psi_{t}, \Psi_{t}$ and $L_{t}$。最后，最优政策为$a_{t}^{*}=L_{t} s_{t | t}$。
