视频地址：https://www.bilibili.com/video/av41393758/?p=8 课程主页地址：http://web.stanford.edu/class/cs224n/ 课程讲义下载地址：https://yunlongs-1253041399.cos.ap-chengdu.myqcloud.com/Books/CS224n/cs224n-2019-notes05-LM_RNN.pdf
Lecture 8 - Language Model and RNN
1. Language Model
1.1 引言
Language Model 是用来计算一系列单词在一句子中同时出现的概率，通常只依赖于前n个单词：\(P\left(w_{1}, \ldots, w_{m}\right)=\prod_{i=1}^{i=m} P\left(w_{i} | w_{1}, \ldots, w_{i-1}\right) \approx \prod_{i=1}^{i=m} P\left(w_{i} | w_{i-n}, \ldots, w_{i-1}\right)\)
比如说，上面的这个等式就对翻译系统来说评判一个翻译序列是否精准特别有用，在现有的Language Model中，对于每一个句子，翻译软件会生成一系列的候选翻译序列，然后可以使用这个模型为各个序列评分，并选择最优的那个作为输出结果。
1.2 n-gram Language Models
2. Recurrent Neural Networks (RNN)
部分参考了https://baozoulin.gitbook.io/neural-networks-and-deep-learning/的笔记
不同于传统的语言模型，循环神经网络可以考虑语料中特定单词之前的所有的单词。 我们先进行如下定义：
- Tx: 代表输入序列的长度
- Ty: 代表输出序列的长度
- $x^{\lt t \gt}$： 在第t时间步时的输入
- $\hat y^{\lt t \gt}$： 在第t时间步时的输出
循环神经网络的网络结构如下：
其中包括了三个全局共享参数：
- $W_{ax}$： 管理着从输出$x^{\lt t \gt}$到隐藏层之间的参数
- $W_{aa}$： 管理着两个隐藏层激活值之间的参数
- $W_{ya}$： 管理着每一个隐藏层激活值$a^{\lt t \gt}$到输出层$\hat y^{\lt t \gt}$之间的参数
$a^{\lt 0 \gt}$一般为零向量，全局共享参数意味着每一层的循环神经网络都只有且只需要更新三个参数。
2.1 RNN的前向传播
将RNN 的神经网络结构图每一隐藏层模块拆开来看，是这样的：
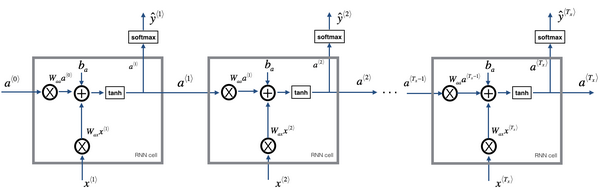其前向传播的过程，从左向右看是这样的：
\(\hat{y}^{\lt t \gt}=g_2\left(W_{y a} \cdot a^{\lt t \gt}+b_{y}\right) \tag {2}\) 此处的$g_1$一般取tanh或relu，$g_2$一般取softmax或sigmoid。
Loss Function：（假设是二分类，若是多分类使用softmax损失）
\[L^{\lt t \gt}\left(\hat{y}^{\lt t \gt}, y^{\lt t \gt}\right)=-y^{\lt t \gt} \log \hat{y}^{\lt t \gt}-\left(1-y^{\lt t \gt}\right) \log \left(1-\hat{y}^{\lt t \gt}\right) \tag {3}\]cost Funtion： \(J(\hat{y}, y)=\sum_{t=1}^{T_{y}} L^{\lt t \gt}\left(\hat{y}^{\lt t \gt}, y^{\lt t \gt}\right) \tag {4}\)
2.2 RNN的反向传播
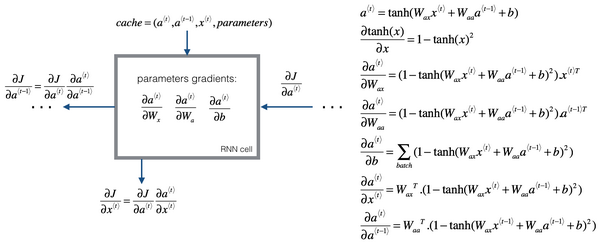
进行反向传播之前，我们先将前向传播的过程倒过来看，即网络结构自顶向下看或自右向左看： \(J(\hat{y}, y)=\sum_{t=1}^{T_{y}} L^{\lt t \gt}\left(\hat{y}^{\lt t \gt}, y^{\lt t \gt}\right) \tag {1}\)
\[L^{\lt t \gt}\left(\hat{y}^{\lt t \gt}, y^{\lt t \gt}\right)=-y^{\lt t \gt} \log \hat{y}^{\lt t \gt}-\left(1-y^{\lt t \gt}\right) \log \left(1-\hat{y}^{\lt t \gt}\right) \tag {2}\] \[\hat{y}^{\lt t \gt}=g_2\left(W_{y a} \cdot a^{\lt t \gt}+b_{y}\right) \tag {3}\] \[a^{\lt t \gt}=g_1\left(W_{a a} \cdot a^{\lt t-1 \gt}+W_{a x} \cdot x^{\lt t \gt}+b_{a}\right) \tag {4}\]因为我们最后的目的是更新参数$W_{aa}、W_{ax} 、W_{ya}$，所以要求出最后的目标函数对这参数参数的梯度：
以$W_{aa}$为例子，根据链式求导法则有：
\[\frac {\partial J}{\partial W_{aa}} = \sum_{t=1}^{T_y} \frac {\partial J}{\partial \hat y^{\lt t \gt}} \frac {\partial \hat y^{\lt t \gt}}{\partial a^{\lt t \gt}} \frac{\partial a^{\lt t \gt}}{\partial W_{aa}} = \sum_{t=1}^{T_y} \frac {\partial J}{\partial a^{\lt t \gt}} \frac{\partial a^{\lt t \gt}}{\partial W_{aa}}\]所以，显而易见，我们只需要求出每一步激活值$a^{\lt t \gt}$的梯度，和每一步中$W_{aa}$关于其激活值$a^{\lt t \gt}$的导数即可求得最终的更新公式。那么如何得到每一步$a^{\lt t \gt}$的梯度呢？
由公式（4）可以得到如下关系：
\[\frac{\partial J}{\partial a^{\lt t-1 \gt}} = \frac{\partial J}{\partial a^{\lt t \gt}} \frac{\partial a^{\lt t \gt}}{\partial a^{\lt t-1 \gt}}\]这里我们假设$g_1=tanh$，可以得到
\[\frac{\partial a^{\lt t \gt}}{\partial a^{\lt t-1 \gt}}=W_{a a}^{T} \cdot\left(1-\tanh \left(W_{ax} x^{\lt t \gt}+W_{aa} a^{\lt t-1 \gt}+b_a\right)^{2}\right)\]所以可以根据链式法则，只需要知道上一步的梯度值，就可以得到本步的梯度值。
那么如何得到每一步中$W_{aa}$关于其激活值$a^{\lt t \gt}$的导数？ 还是根据公式（4）得到：
\[\frac{\partial a^{\lt t \gt}}{\partial W_{aa}}=\left(1-\tanh \left(W_{a x} x^{\lt t \gt}+W_{aa} a^{\lt t-1 \gt}+b\right)^{2}\right) a^{\lt t-1 \gt T}\]同理，其他参数也是可以使用类似的过程来推导出更新公式，我们所需要做的就是，保留前向传播中每一步的参数，传递下一步的梯度。
2.3 梯度剪切（gradient clip）
从上面的反向传播推导过程中可以看到，越往前计算梯度值，其梯度的累乘项就越多，举个例子：如果我们$g_1$激活函数选用relu，并且偏差项b为0，并假设参数W和x均大于1，这样我们可以得到$a^{\lt t \gt} = W_{aa}a^{\lt t-1 \gt}+W_{ax}x^{\lt t \gt} $，根据relu函数同样可以到梯度值 \gt1。这样的梯度累乘下去，就会造成梯度成指数倍增长，导致参数无法有效更新。
Gradient clip 可以通过给梯度设定阈值的方法，来将梯度控制在一定范围内，来防止梯度爆炸：
- 设定超参数梯度阈值grad_clip的值
- 对梯度进行L2范数的计算$|g|_ 2=\sqrt{\sum_{i} g_{i}^{2}}$
- 然后再比较梯度的L2范数和设定的grad_clip的大小
- 如果$|g|_ {2}$更大 ，缩放因子Scale $=g r a d_{-} c l i p /|g|$
- 如果grad_clip更大， 则记缩放因子scale为1
- 最后将梯度乘上缩放因子scale 来得到需要的梯度来更新参数
2.4 循环神经网络的类型
按照输入- \gt输出的个数，目前RNN包含以下几个类型：
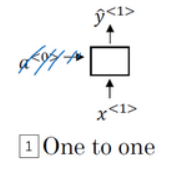
- 一对一，当去掉$a^{\lt 0 \gt}$时它就是一种标准类型的神经网络
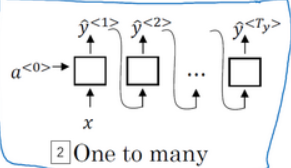
- 一对多，比如音乐生成或者序列生成
- 多对一，如是情感分类的例子，首先读取输入，一个电影评论的文本，然后判断他们是否喜欢电影还是不喜欢
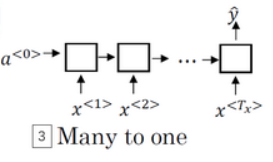
- 多对多 ，如命名实体识别，$T_{x}=T_{y}$
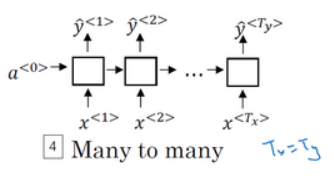
- 多对多，如机器翻译，$T_{x} \neq T_{y}$
3. 双向循环神经网络（Bidirectional RNN）
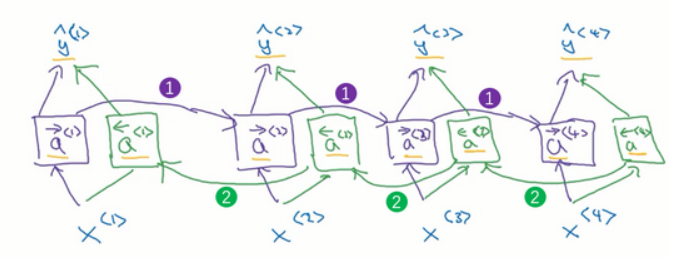\(\hat{y}=g\left(W_{g}\left[a^{\rightarrow\lt t \gt}, a^{\leftarrow\lt t \gt}\right]+b_{y}\right)\)
BRNN的前向传播过程即需要从左向右计算一次激活值（1），也需要从右向左计算一次激活值（2），只有等每个单元的右向激活值和左向激活值都计算完毕后，才可以进行预测计算$\hat y{\lt t \gt}$。
而图中的每个激活单元可以选用GRU单元也可以选用LSTM单元。
缺点是需要完整的数据的序列才能预测任意位置。
4. 深层循环神经网络（Deep RNNs）
一个三层的RNN网络如图：
另一种深层RNN网络，结构是每个输出层上还有一些垂直单元：
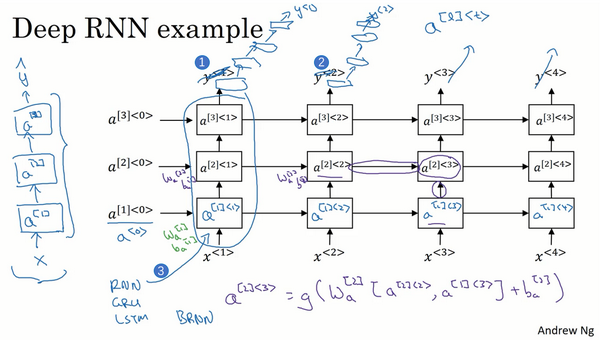即把输出去掉（编号1），在每一个上面堆叠循环层，然后换成一些深的神经网络层，这些层并不水平连接，只是一个深层的网络，然后用来预测$\hat y^{\lt t \gt}$
