请咨询作者同意后转载。
Neural Network-based Graph Embedding for Cross-Platform Binary Code Similarity Detection(Gemini)
| 期刊/会议: | CCS(A类) |
|---|---|
| 发表时间: | 2017年12月3日 |
| 发表机构: | 上交, California, Berkeley |
Genius的缺点
- 编码本生成代价十分昂贵,因为需要对训练集中的每对控制流图都要进行成对的图匹配,然后在进行聚类,所以编码本的质量会收到训练集的大小所限制。
- 图嵌入所需要的总运行时间和编码本的大小呈线性增长,限制了编码本不能太大。
- 这种方法的精确度受二分图匹配的质量所限制。
具体实现
1.代码相似度嵌入问题
给定两个二进制函数$f_1,f_2 $,$\pi(f_1,f_2)=1$表示这两个程序相似,$\pi(f_1,f_2)=-1$表示这两个程序不相似。
代码相似度嵌入问题的目标是寻找到一个映射$\phi$,来将函数$f$的ACFG映射到向量表示$\mu$,且这种嵌入应当能够捕捉足够的信息来用于检测相似性函数。因此,刚给定一个容易计算的相似性函数$Sim()$(例如余弦函数),对与两个二进制函数$f_1$,$f_2$,当$\pi(f_1,f_2)=-1$时$Sim(\phi(f_1),\phi(f_2))$会很大,小则相反。
相比于Genius这样做的优点:能够保证高效的计算,两个向量之间的相似度计算代价很小,并不需要进行代价昂贵的图匹配算法。
2.方法概述
将映射$\phi$设计成一个神经网络,利用图嵌入方法:Structure2vec,其输入是ACFG。但是Structure2vec是用来解决分类问题,需要标签,但是我们的嵌入问题并不需要标签,所以需要设计一个新的方法来训练图嵌入网络进行相似性检测。
对应的解决方案是,不训练图嵌入网络$\phi$去做特定的预测任务,而是训练$\phi$来区别两个输入的ACFG的相似程度。尤其是设计了Siamese结构采取图作为输入,并输出其相似度。
但是训练Siamese网络需要大量的有标签成对数据集,为了采取default 策略: 将由相同原代码编译得到的函数标记为相似,相反则不相似。由此,我们可以得到一个很大的数据集。
3.图嵌入网络
给定ACFG$g=\langle\mathcal{V}, \mathcal{E}\rangle$,其中$\mathcal{V}$和$\mathcal{E}$各自代表顶点集和边集,对于每个顶点$v$定义其额外的属性为$x_v$也就是ACFG的特征。因此,图嵌入网络首先会对每个节点$v$计算其$p$维的特征$u_v$,而后整个图的$u_g$则可以看成是每个节点向量的累加$\mu_{g}=\sum_{v \in \mathcal{V}}\left(\mu_{v}\right)$。
基本的Structure2vec方法 在一些步数的迭代之后,网络会对每个节点生成新的考虑了图结构和不同节点特征间长范围交互的特征表示 。
\[\mu_{v}^{(t+1)}=\mathcal{F}\left(x_{v}, \sum_{u \in \mathcal{N}(v)} \mu_{u}^{(t)}\right), \forall v \in \mathcal{V}\]其中$\mathcal{F}$为一般非线性映射,将会在之后进行明确。
从上面的公式中可以看出来,嵌入更新是基于图的结构进行的,且新的一轮要在上一轮都结束之后才能开始。并且还能看出来,进行的迭代次数越多,节点所能传播的距离就越远。最后如果上式进行了T轮迭代,那么每个节点的嵌入向量$\mu_{v}^{(T)}$将会包含其周围T-hop节点的信息。
参数化 我们将$\mathcal{F}$设计成如下的形式:
\[\mathcal{F}\left(x_{v}, \sum_{u \in \mathcal{N}(v)} \mu_{u}\right)=\tanh \left(W_{1} x_{v}+\sigma\left(\sum_{u \in \mathcal{N}(v)} \mu_{u}\right)\right)\]其中$x_v$是图中基本快特征的d维向量,$W_1$是$d \times p$矩阵,p是嵌入向量的大小。定义非线性变换$\sigma(\cdot)$为n层全链接神经网络。
\[\sigma(l)=\underbrace{P_{1} \times \operatorname{ReLU}\left(P_{2} \times \ldots \operatorname{ReLU}\left(P_{n} l\right)\right)}_{n \text { levels }}\]其中$P_i$是$p \times p$的参数矩阵。
4. Siamese Architecture
Siamese采用2个Structure2vec网络作为输入,每个网络输出其输入ACFG的嵌入$\phi\left(g_{i}\right)$,而整个Siamese网络的输出是两个ACFG嵌入向量的预先距离。
网络结构如图:
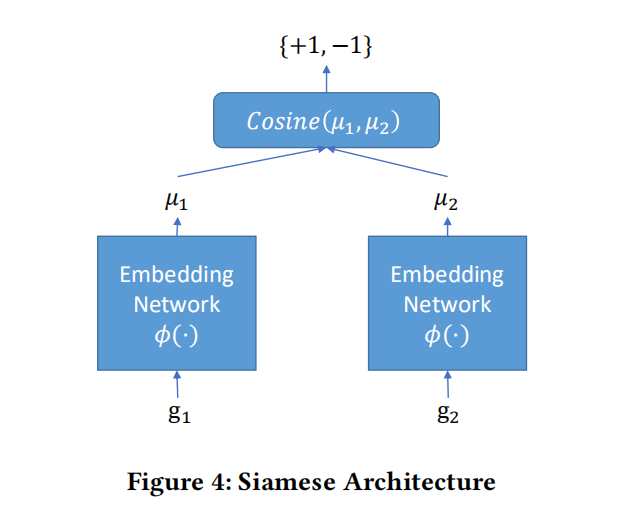
而所采用的损失函数如下:
\[\min _{W_{1}, P_{1}, \ldots, P_{n}, W_{2}} \sum_{i=1}^{K}\left(\operatorname{Sim}\left(g_{i}, g_{i}^{\prime}\right)-y_{i}\right)^{2}\]5.Task-independent Pre-training and Task-specific Re-training
因为Siamese的训练需要大量的标签数据集,所以就使用文中提及的default策略 。
Task-independent Pre-training. 为了能够让我们与训练的模型能够应用与大多数任务,所以我们为每个函数生成的向量应当能够捕获不同平台和编译器之间的不变性特征。 所以,将收集到的源代码通过不同的平台和编译器进行编译,由相同源代码编译得到的标记为1,不相同原代码编译得到的标记为-1,就可以得到大量的预训练样本。
Task-specific Re-training. 在预训练完成后,我们使用额外的一小部分由专家知识组成的数据集进行再训练,来更高效的调整模型的参数。
实验评估
Baseline
两种baseline评估方法:
- Bipartite Graph Matching (BGM): 给定2个函数,直接计算出他们使用二分图匹配算出的ACFG的相似性分数。
- Codebook-based Graph Embedding (Genius).: Genius方法提供了图嵌入方法的baseline。
数据集
Dataset I: 用于神经网络训练和Baseline比较,由源代码编译后的二进制程序组成。
Dataset II: Genius中使用的33045个镜像。
Dataset III: 从数据集Ⅱ中随机选取了16个镜像,用于测试不同规模ACFG下的效率。
Dataset IV: Gunius中使用的漏洞数据集。
Accuracy
(a)在数据集I上进行测试,(b)在I中都至少包含10个节点的ACFG对上进行测试,(c)在I中剩下的数据集中进行测试。

Efficiency
S代表单线程,M代表多线程
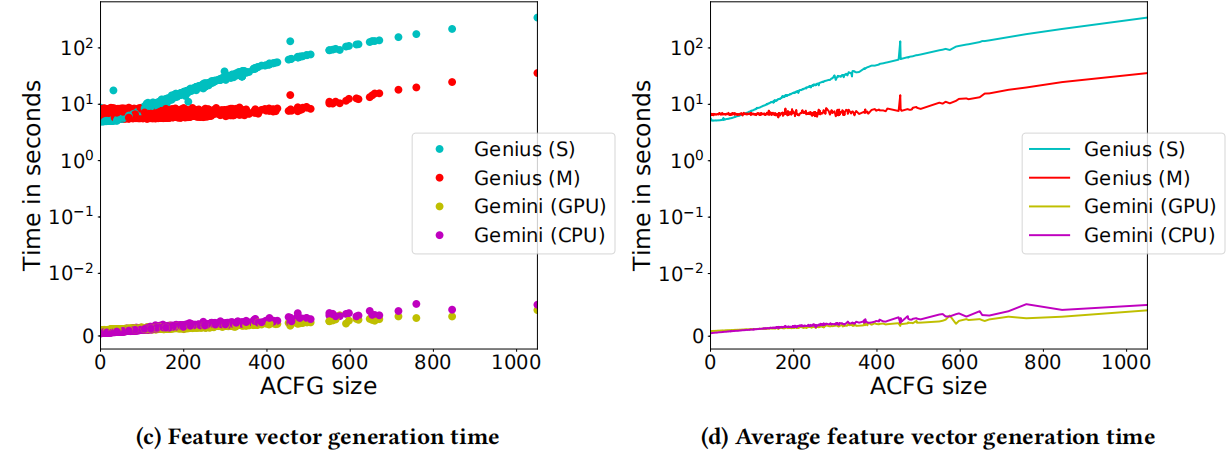
Accuracy of Task-specific Retrained Model using Real-world Datase
采用与Genius同样的方法,从数据集Ⅳ中选择相同的两个漏洞函数,在数据集Ⅰ中进行搜寻,在top-50中,Gemini可以得到80%的准确率,而Genius只有20-50%。