Properties of Networks & Random Graph Models
1. 网络的属性：如何来度量一个网络
For 无向图，对于有向图很容易泛化
1.1 度分布(Degree Distribution)
Degree distribution $P(k)$: 一个随机选取的节点，其度为k的概率。
$N_k$为度为k的节点个数，$P(k) = N_k/N$.
1.2 路径长度(Path Length)
路径长度 两个点之间的最短距离。
图的直径(Diameter)：图中的最大路径长度。
平均路径长度:对于强连通图来说： \(\bar{h}=\frac{1}{2 E_{\max }} \sum_{i, j \neq i} h_{i j}\) 其中$h_{ij}$为节点i和节点j之间的距离，$E_{max}=n(n-1)/2$为图可能存在的最多边数。
1.3 聚类系数(Clustring Coefficient)
用来评估节点的邻居们之间的连通性。 当节点i的度表示为$k_i$时，此节点的聚类系数为： \(C_i = \frac{2e_i}{k_i(k_i-1)}\)
其中，$e_i$为节点i的邻居中存在的边数。
平均聚类系数： \(C = \frac{1}{N} \sum^N_i C_i\)
1.4 连通成分大小(Connected components)
为最大连通子图中节点的个数。
2.真实网络的属性度量
对MSN中的网络进行了统计。
3.Erdös-Renyi Random Graphs
为了回答上面的问题，因此，我们需要为图进行建模。
3.1 随机图模型
有两种变体：
- $G_{np}$： 有n个节点，且每条边都以概率$p$出现的无向图
- $G_{nm}$: 有n个节点，随机采样m条边的无向图。
后面我们主要使用第一种形式。需要注意的是相同的n和p值可以具有多种的图表现形式。
3.2 随机图模型的属性度量
3.2.1 随机图的度分布
随机图的度分布是二项式的，如下图：
原因很简单：从N-1个节点中随机选择k个节点，选中的概率为p，没选中的概率为(1-p)
3.2.2 随机图的聚类系数
3.2.3 随机图的属性总结
路径长度和最大连通图大小的证明省略。
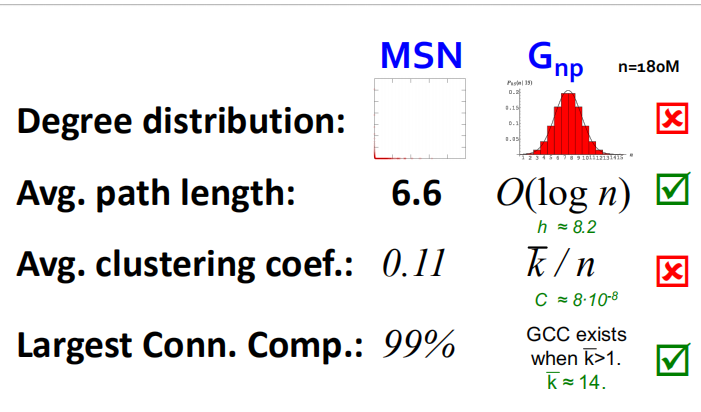从图中可以看出来，随机图模型与真实世界网络之间存在较大的差距，因此随机图模型并不能很好的反映出真实网络。
4. The Small-World Model
4.1 聚类系数意味着边的局部性
从上面的例子可以看出来，MSN真实网络的聚类系数比随机图模型大了7阶，并且老师还举了其他几个例子，都发现真实网络的聚类系数要大的多。
为此，还发现当将一个低聚类系数的网络变成高聚类系数的网络，网络中将会出现局部结构，聚类意味着边的局部性，而随机性则会在不同节点之间增加短接边。
Small-World model
当不断的增加p的概率，就可以得到一个合适的参数区间，同时具有高聚类系数和低路径长度，来模拟真实世界。
总结
- 提供small-world的思想，和聚类之间的短接
- 捕捉了一些真实网络的结构特性
- 为真实网络的高聚类系数做出了解释
- 但没有提供正确的度分布
5.Kronecker graphs:
提出了一种自相似性的观点，认为目标的各部分之间具有相似性。
而利用Kronecker积可以生成具有这种自相似性的矩阵。
5.1 Kronecker graphs模型
定义：两个图之间的Kronecker 乘积为其邻接矩阵之间的乘积
而Kronecker graphs则是通过对一个初始矩阵迭代进行Kronecker 乘积生成。
5.2 Stochastic Kronecker graphs
- 创建一个$N_1\times N_1$的概率矩阵$\theta_1$
- 对其计算k次Kronecker乘积得到$\theta_k$
- 对于$\theta_k$中的每条边$(u,v)$具有概率$p_{uv}$
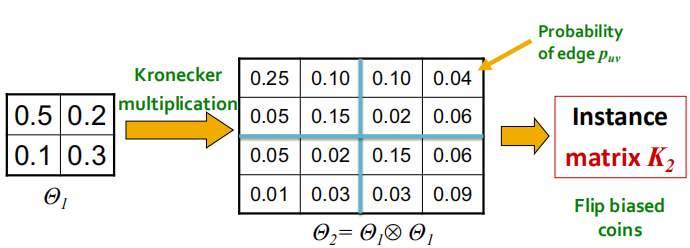
实验结果显示，此模型与真实网络非常相似
