视频地址：https://www.bilibili.com/video/av49432977/?p=20 课程主页地址：http://cs229.stanford.edu/
Lecture 20 -Policy search , Pegasus
1. Policy search
在策略搜索算法中，提出了两个定义，如下：
- 定义策略集$\Pi$作为所有可能策略的合集，我们通过对集合$\Pi$进行搜索，找到可以获得最优结果的策略$π$
- 随机策略为$π:S\times A->R$状态和动作到实数的一个映射，$\sum \pi(s, a)=1$，$π(s,a)>0$
策略搜索的思想如下： 从初始状态$s_0$开始，随机采取动作作形成一（状态–动作）序列，来穷举策略寻找最大的回报payoff的期望。
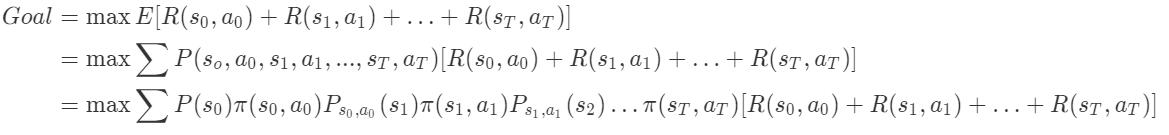
其中，payoff为 $[R(s_0, a_0)+R(s_1, a_1)+\ldots+R(s_T, a_T)]$
策略搜索算法的流程如下：
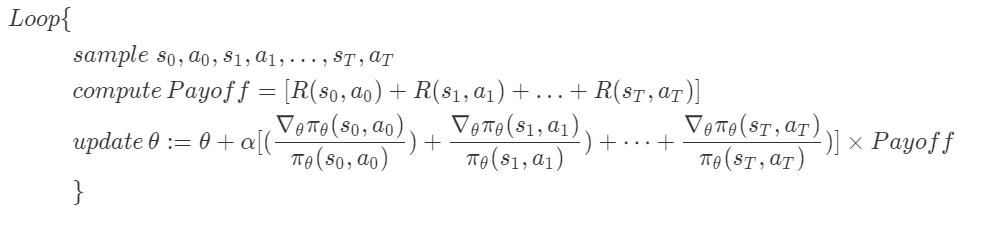其中参数更新的推导就省略了，对目标函数使用随机梯度上升算法即可得到。
需要注意到算法中的，$[(\frac {\nabla_θ\pi_θ(s_0,a_0)}{\pi_θ(s_0,a_0)})+\frac {\nabla_θ\pi_θ(s_1,a_1)}{\pi_θ(s_1,a_1)})+ \dots +\frac {\nabla_θ\pi_θ(s_T,a_T)}{\pi_θ(s_T,a_T)})] \times Payoff = \nabla _θE[Payoff]$
2. Pegasus
Pegasus算法全称为Policy Evaluation of Gradient And Search Using Scenarios，使用场景进行梯度和搜索的策略评估算法。
这一算法使用了之前模拟器的思想，即将生成下一个状态的过程抽象为对一个模拟器输入当前状态和当前动作的过程，由模拟器输出下一状态 。但更广泛的，这一算法将当前动作产生的过程也视为一个黑盒，即对黑盒输入当前的状态，黑盒便输出当前的动作。 我们希望通过拟合模拟及结果和政策之前的曲线，选择正确率最高的策略π。
但由于模拟器会产生一定的误差（我们通过随机值描述这一误差），因此即使给定相同的状态和动作，每一次模拟器生成的结果都是不同的，所以即便我们对某一次模拟器生成的结果不产生训练误差，下一次训练的结果便是不同的，依然会产生误差，这一问题的根源就来自于我们设立的随机数。但我们不能将随机数去掉，因为他们描述了状态转移过程中噪声的影响。为了解决这一问题，我们将产生一次随机数，然后将这些随机数固定下来进行之后的过程。
作者：禛zhen 来源：CSDN 原文：https://blog.csdn.net/knight_wzz/article/details/53053516
