请咨询作者同意后转载。
Discriminative Embeddings of Latent Variable Models for Structured Data(structure2vec)
代码实现博客：https://blog.csdn.net/haotaoshu/article/details/79201659 https://github.com/Hanjun-Dai/graphnn.
| 期刊/会议： | ICML（A类） |
|---|---|
| 发表时间： | 2016年 |
| 发表机构： | Georgia Institute of Technology |
前言
介绍了kernel方法在处理结构化数据上取得的进展，可以方便、便捷、有效的处理结构化对象（字符串、树、图）。
但是在如今的大数据时代，这些方法都不能有效的去处理数百万的数据，并举了两个例子：BOS kernel和GM kernel来说其局限性。
在这片文章汇总，作者希望能够对使用graphical models作为kernel或者特征空间设计这个idea做一些修正，并能使其扩展到数百万的结构化数据。 其主要思想是：将每个结构化的数据点建模为潜在变量模型，然后将graphical model嵌入到特征空间，并且使用embedding空间中的内积来定义kernels，通过最小化由标签信息定义的经验误差来定义特征空间。
structure2vec算法和其他kernel 消息传递的算法主要不同点在于：：
- 可以学习结构化数据的相似性度量。
- 使用判别信息来学习非线性映射
- can run in a mean field update fashion（没太懂）
并说明了其在在处理大数据时，卓越的性能表型。
背景
我们定义$X$为域$\mathcal{X}$下的随机变量，$x$为$X$的一个实例化表示，定义$\mathcal X$的密度函数为$p(X)$，多元随机变量$X_{1}, X_{2}, \ldots, X_{\ell}$的联合概率密度为$p\left(X_{1}, X_{2}, \ldots, X_{\ell}\right)$。
为了简化符号表示，我们假设对于所有的$X_{t}, t \in[\ell]$的域都是相同的，但是在应用时不一定。在本例中，$\mathcal X$为离散域，所以密度函数应当被理解为概率函数，积分理解为累加。
另外，我们定义$H$为域$\mathcal H$和分布$p(H)$下的隐藏变量。
kernel 方法： 假设结构化数据被表示为$\chi \in \mathcal{G}$，kernel函数为$k\left(\chi, \chi^{\prime}\right): \mathcal{G} \times \mathcal{G} \mapsto \mathbb{R}$，并且kernel矩阵需要为半正定矩阵。kernel方法的一个特点是，可以在不需要访问原数据点来学习映射的情况下，直接使用其kenel值在高维空间中工作。
kernel for structured data: 每个kernel函数都等同于一些特征映射$\phi(\chi)$，其中kernel函数可以被表达成特征映射间内积的形式，比如$k\left(\chi, \chi^{\prime}\right)=\left\langle\phi(\chi), \phi\left(\chi^{\prime}\right)\right\rangle$。
而对于结构化的为输入域，可以使用子结构的数量来设计kernels。例如，spectrum kernel 对于两个序列$\mathcal X$和$\mathcal X’$被定义为：
其中$S$是可能序列的集合，$(s \in \chi)$统计了子序列在$x$中出现的次数。在本例中，特征映射$\phi(\chi)=\left(\left(s_{1} \in \chi\right), \left(s_{2} \in \chi\right), \ldots\right)^{\top}$相当于一个$|S|$维的向量。
相似的，对于两个图$\mathcal X$和$\mathcal X’$作为输入的praphlet kernel来说，也可以被定义为上式，不过现在$S$是可能子图的集合，$(s \in \chi )$为子图在$\mathcal X$中出现的次数。这一类的kernels被称为”bag of structures”(BOS)kernel。
Hilbert Space Embedding of Distributions: Hilbert空间嵌入是将分布映射到潜在的无限维特征空间中：
\[\mu_{X}:=\mathbb{E}_ {X}[\phi(X)]=\int_{\mathcal{X}} \phi(x) p(x) d x: \mathcal{P} \mapsto \mathcal{F}\]其中这个分布被映射到它期待的特征映射中，例如特征空间中的一个点。这些分布的kernel embedding具有丰富的表征力。另外还有些kernel可以使映射变成单射的，这样就可以将不同的分布映射到不同的特征空间中去，比如RBF kernel。
相对的，我们可以将密度$p(X)$的单射embedding $\mu_X$作为其充分统计量，这样我们所需要从密度中获得的信息都被保存在了$\mu_X$中：这样$\mu_X$就可以独一无二的恢复出$p(X)$，对$p(X)$的任何操作可以通过对$\mu_X$做对应的操作来获得相同的结果。比如，这个属性可以允许我们只使用embedding就可以计算出密度的函数结果。
\[f(p(x))=\tilde{f}\left(\mu_{X}\right)\]上式中$\hat f$是对$\mu_X$对应的函数。
3. Model for a Structured Data Point
普遍来说，我们假设每个结构化的数据点$\mathcal X$为一个graph，节点集合$\mathcal V = \lbrace 1,\dots,V \rbrace$，边集合$\mathcal{E}$。并且我们将使用$x_i$来表示节点i的属性值。
我们将结构化的数据点$\mathcal X$建模为graphical model中的一个实例，更确切地说，我们将graph中每个节点的标签建模为一个变量$X_i$，并且与一个额外的隐变量$H_i$相联系。然后我们将在这些随机变量集合上定义一个成对的马尔科夫随机场
\[p\left(\left\lbrace H_{i}\right\rbrace ,\left\lbrace X_{i}\right\rbrace \right) \propto \prod_{i \in \mathcal{V}} \Phi\left(H_{i}, X_{i}\right) \prod_{(i, j) \in \mathcal{E}} \Psi\left(H_{i}, H_{j}\right)\]马尔科夫随机场介绍：https://blog.csdn.net/hohaizx/article/details/82868843
其中$\Psi$ and $\Phi$分别为非负节点和边的的势函数。在这个模型中，这些变量被输入数据点的图结构所连接，这相当于说，我们直接使用输入数据的图结构作为一个无向图模型的条件独立结构。Figure 1阐释了为了字符串和graph建立graphical model的例子。
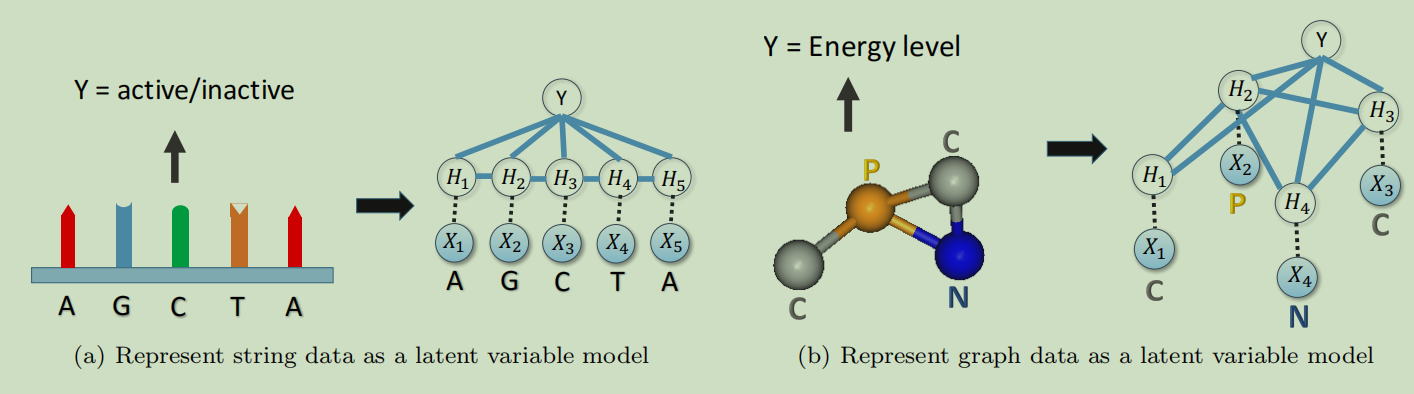
4.Embedding Latent Variable Models
我们将使用一个特征映射$\phi\left(H_{i}\right)$来对隐变量的后验概率进行嵌入，例如：
\(\mu_{i}=\int_{\mathcal{H}} \phi\left(h_{i}\right) p\left(h_{i} \|\left\lbrace x_{i}\right\rbrace \right) d h_{i}\)
$\phi\left(H_{i}\right)$和$\operatorname{MRF} p\left(H_{i} |\left\lbrace x_{i}\right\rbrace \right)$中参数的精确形式在当前是不固定的， 我们将在稍后使用监督信号来学习它们作为最终判别目标。现在我们假设$\phi\left(H_{i}\right) \in \mathbb{R}^{d}$在一个有限维的特征空间中，并且精确的$d$值将会在之后的实验中通过交叉验证来确定。
然而对于一般的图任务来说，计算这样的embedding是非常具有挑战性的：其涉及一个我们需要对所有变量（除了$H_i$）进行积分从而进而推导的graphical model。例如：
\[p\left(H_{i} |\left\lbrace x_{i}\right\rbrace \right)=\int_{\mathcal{H}^{V-1}} p\left(H_{i},\left\lbrace h_{j}\right\rbrace |\left\lbrace x_{j}\right\rbrace \right) \prod_{j \in \mathcal{V} \backslash i} d h_{j}\]只有在图结构为树的时候，我们才可以通过消息传递来进行有效的精确计算。因此在一般的案例中，会采用像mean field inference and loopy belief propagation (BP)这样的近似推导算法。
4.1 Embedding Mean-Field Inference
后面很难看懂了，涉及的理论有点深了，从来没接触过，就直接翻译过来看看吧。
vanilla mean-field inference试图去使用独立密度成分的乘积来去近似$p\left(\left\lbrace H_{i}\right\rbrace |\left\lbrace x_{i}\right\rbrace \right)$，其中$q_{i}\left(h_{i}\right) \geqslant 0$是有效密度函数，并且$\int_{\mathcal{H}} q_{i}\left(h_{i}\right) d h_{i}=1$。
例外，这些密度函数成分是通过最小化如下的 variational free energy来发现的：
我们发现为了求解上面的优化问题，需要对所有的$ i \in \mathcal{V}$满足下面的不动点等式：
\[\begin{aligned} \log q_{i}\left(h_{i}\right) &=c_{i}+\log \left(\Phi\left(h_{i}, x_{i}\right)\right)+\sum_{j \in \mathcal{N}(i)} \int_{\mathcal{H}} q_{j}\left(h_{j}\right) \log \left(\Psi\left(h_{i}, h_{j}\right) \Phi\left(h_{j}, x_{j}\right)\right) d h_{j} \\ &=c_{i}^{\prime}+\log \Phi\left(h_{i}, x_{i}\right)+\sum_{j \in \mathcal{N}(i)} \int_{\mathcal{H}} q_{j}\left(h_{j}\right) \log \Psi\left(h_{i}, h_{j}\right) d h_{j} \end{aligned}\]其中，$c_{i}^{\prime}=c_{i}+\sum_{j \in \mathcal{N}(i)} \int q_{j}\left(h_{j}\right) \log \Phi\left(h_{j}, x_{j}\right) d h_{j}$。这里$\mathcal{N}(i)$为变量$H_{i}$在graphical model中的邻居集合,$c_i$是一个常量。
不动点等式暗示了$q_{i}\left(h_{i}\right)$是一系列邻居marginals$\left\lbrace q_{j}\right\rbrace _{j \in \mathcal{N}}(i)$的函数，例如：
\[q_{i}\left(h_{i}\right)=f\left(h_{i}, x_{i},\left\lbrace q_{j}\right\rbrace _{j \in \mathcal{N}(i)}\right)\]如果对每个marginal $q_i$，我们有一个单射embedding
\[\widetilde{\mu}_{i}=\int_{\mathcal{H}} \phi\left(h_{i}\right) q_{i}\left(h_{i}\right) d h_{i}\]那么根据之前提到的单射的属性，我们可以从embedding point的视角来同等的表达上面的不动点等式，例如：$q_{i}\left(h_{i}\right)=\hat{f}\left(h_{i}, x_{i},\left\lbrace \tilde{\mu}_ {j}\right\rbrace _{j \in \mathcal{N}(i)}\right)$，并且我们可以将函数$\hat f$转化成对等的操作$\tilde{\mathcal{T}}$：
\[\tilde{\mu}_ {i}=\tilde{\mathcal{T}} \circ\left(x_{i},\left\lbrace \tilde{\mu}_ {j}\right\rbrace _{j \in \mathcal{N}(i)}\right)\]为了得到上式的mean field嵌入，函数$\hat f$和操作$\tilde{\mathcal{T}}$在势函数$\Psi, \Phi$上有复杂的依赖关系，并且特征映射$\phi$是未知的，需要从数据中学习。但是我们并不首先学习出$\Psi和\Phi$，然后再求解出$\tilde{\mathcal T}$这种做法，我们将寻求一种不同的路线：直接对$\tilde{\mathcal T}$参数化，然后通过监督信号来学习它。
至于这个参数化，我们将认为$\tilde \mu_i \in R^d$中的$d$是个超参数且可以使用交缠验证发来选择。对于$\tilde{\mathcal T}$，可以使用任何的非线性映射，比如说我们可以将其参数化为一个神经网络：
\[\tilde{\mu}_ {i}=\sigma\left(W_{1} x_{i}+W_{2} \sum_{j \in \mathcal{N}(i)} \tilde{\mu}_{j}\right)\]其中$\sigma$是RELU激活函数，$W_1和W_2$的行数为$d$。在这样的参数化下，在embedding 空间中的mean field 迭代更新过程如算法1所示。我们同样也可以乘以$\tilde \mu_i$和$V$来rescale message embedding的范围，如果需要的话。
对于这个具体流程，我觉得VulSeeker中Function Semantics Generation部分解释的很形象：
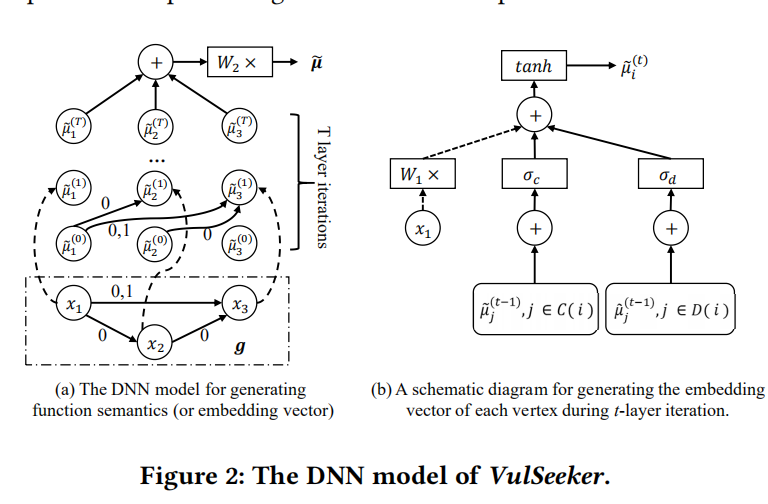
4.2 Embedding Loopy Belief Propagation
Loopy belief propagation是另一个变分推断方法，其本质上通过考虑成对的关系来优化Bethe free energy。
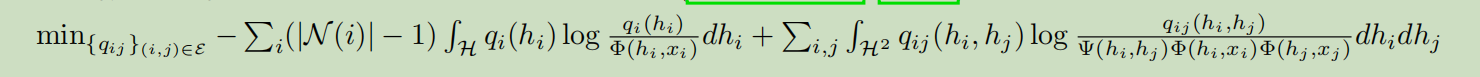其服从pairwise marginal一直约束：
并且$\int_{\mathcal{H}} q_{i}\left(h_{i}\right) d h_{i}=1$。对于所有的$(i,j)\in mathcal E$,我们可以得到上面优化问题的所有不动点条件：
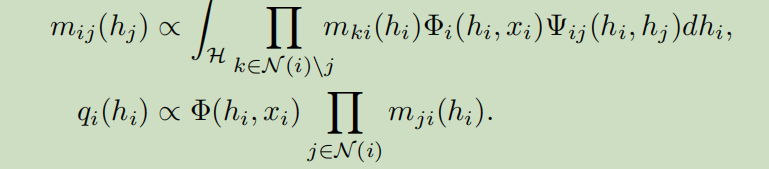其中$m_{ij}(h_j)$是从节点i到j的中间结果，另外，$m_{ij}(h_j)$是一个非负函数，所以其也可以被标准化为一个密度函数，因此也可以被embeded。
和mean field例子相似，上式也暗示着消息$m_{ij}(h_j)$和marginals $q_i(h_i)$是来自邻居消息的函数，例如：
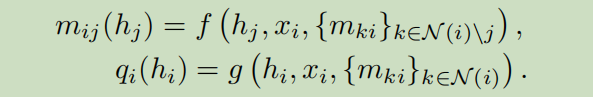
在假设对于每个消息$\tilde{\nu}_ {i j}=\int \phi\left(h_{j}\right) m_{i j}\left(h_{j}\right) d h_{j}$和每个marginal$\widetilde{\mu}_ {i}=\int \phi\left(h_{i}\right) q_{i}\left(h_{i}\right) d h_{i}$都存在一个单射embedding，同样利用单射的属性，可以将这些消息和marginals从embedding 的视角来表达：
和mean field 的例子一样，我们对loopy BP EMBEDDING使用参数化，例如神经网络，假设$\widetilde{\nu}_ {i j} \in \mathbb{R}^{d}, \widetilde{\mu}_{i} \in \mathbb{R}^{d}$：
其embedding过程如算法2所示：
当然，对于非线性映射$tilde{\mathcal T_1}和\tilde{\mathcal T_2}$，我们仍然可以采用其他的非线性函数。
5. Discriminative Training
只需要使用的话，简单的了解下训练过程就够了吧，具体的细节可以看原论文。
6.实验
这里展示下在Graph 数据集下分类的表现，作者采用了5个医学方面的数据集(比如蛋白质、药物组成之类的)，来做多标签或二分类任务。
其数据集的结构如下图这个例子：
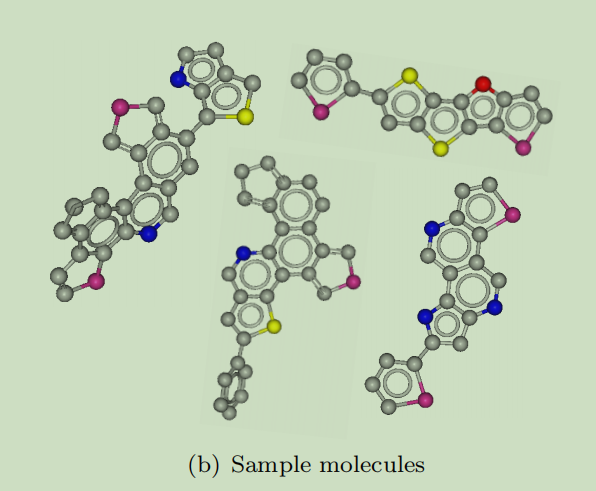
其实验结果如下：
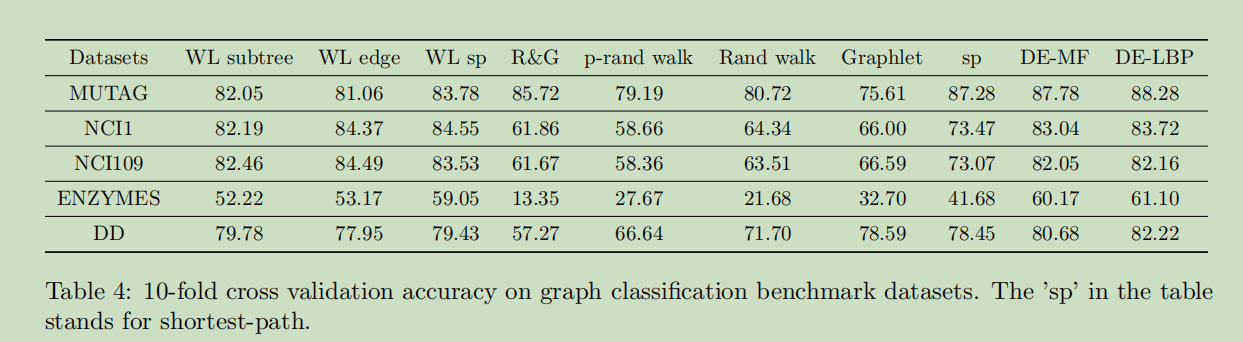可以看到其准确度相较于以前的方法还是有较大的提升的。
